
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Средний арифметический и средний гармонический индексы.
|
|
Приведенные выше формулы расчета индексов называются агрегатными. Расчет индексов по агрегатным формулам возможен, если есть полные данные о физическом объеме продукции и о ценах как на уровне отчетного так и базисного периодов. В реальной действительности полные данные имеются не всегда. В таких случаях приходится исчислять индексы как среднюю взвешенную величину из индивидуальных индексов.
Вопрос о выборе формы средней и системы весов при расчете индекса как среднего из индивидуальных решается на основе общего правила: агрегатный индекс – основная форма всякого индекса. Следствие этого правила – средний из индивидуальных индексов будет тогда правильным, когда он тождественен агрегатному индексу. Это означает, что средние из индивидуальных индексов не самостоятельные индексы, а преобразованная форма агрегатного индекса. При исчислении средних индексов могут быть использованы только две формы средних: средняя арифметическая и средняя гармоническая.
Пример 2
Имеются следующие данные о продаже товаров:
| Товарные группы | Продано товаров в базисном периоде, млн. руб. | Индексы количества проданных товаров в отчетном периоде по сравнению с базисным |
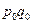
| 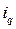
| |
| Обувь | 0, 95 | |
| Посуда | 1, 10 | |
| Ковры | 1, 20 |
Требуется определить общий индекс физического объема товарооборота.
Агрегатная формула индекса физического объема товарооборота:
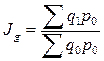 .
.
В нашем примере есть сведении о 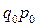 . Кроме того, мы имеем индивидуальные индексы количества проданных товаров по каждой товарной группе. Как известно
. Кроме того, мы имеем индивидуальные индексы количества проданных товаров по каждой товарной группе. Как известно 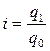 .
.
Из данной формулы выразим 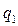 :
: 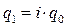 и подставим это значение
и подставим это значение 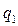 в числитель агрегатной формулы индекса. Тогда будем иметь:
в числитель агрегатной формулы индекса. Тогда будем иметь:
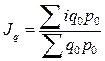 ,
,
где 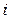 - индивидуальный индекс физического объема товарооборота;
- индивидуальный индекс физического объема товарооборота;
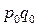 - товарооборот базисного периода.
- товарооборот базисного периода.
В данном случае используем средний арифметический индекс.
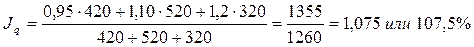
Таким образом, количество проданных товаров увеличилось в отчетном периоде по сравнению с базисным на 7, 5%.
Пример 3.
Имеются следующие данные о реализации товаров:
| Товарные группы | Товарооборот отчетного периода, млн.руб. | Изменение цен в отчетном периоде по сравнению с базисным, % |
| Одежда | +10 | |
| Ткани | -5 | |
| Обувь | -15 |
Вычислить индивидуальные и общий индексы цен.
Индивидуальные индексы:
| На одежду | 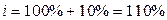
|
| На ткани | 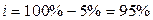
|
| На обувь | 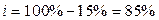
|
Агрегатная формула общего индекса цен:
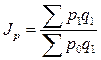
Объем товарооборота 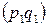 по каждой товарной группе имеем по условию задачи.
по каждой товарной группе имеем по условию задачи.
Из формулы индивидуального индекса цен 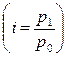 выражаем
выражаем 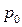 :
: 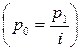 и это значение
и это значение 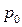 подставляем в агрегатную формулу
подставляем в агрегатную формулу 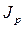 .
.
Тогда
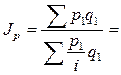
 .
.
Это формула среднего гармонического индекса.
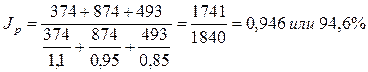 , т.е. в среднем цены снизились на 5, 4%.
, т.е. в среднем цены снизились на 5, 4%.
4. Индексный анализ динамики средних уровней качественных показателей.
Средние уровни многих экономических явлений исчисляются на основе групповых средних. Например средняя себестоимость изделия А по двум предприятиям определяется исходя из средней себестоимости изделия А на каждом предприятии взвешенной по количеству изделий, произведенных на данном предприятии, т.е.
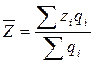
Индекс динамики средней себестоимости изделия А имеет следующую формулу:
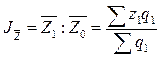 :
: 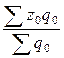 .
.
На величину этого индекса оказывают влияние два фактора – изменение себестоимости на каждом предприятии и изменение объема продукции (удельного веса, структуры) отдельных предприятий. Поскольку в данном индексе используются веса разных периодов, то этот индекс называют индексом переменного состава. Индекс переменного состава характеризует изменение средней величины качественного показателя по всей совокупности:
Для выявления влияния на изменение средней себестоимости изменения самой себестоимости рассчитывают индекс постоянного состава. который характеризует изменение величины качественного показателя в среднем по отдельным объектам совокупности: Чтобы исключить влияние структурных сдвигов на изменение средней себестоимости, среднюю себестоимость в базисном периоде корректируют на структуру фактического выпуска продукции. В общем виде формула индекса себестоимости фиксированного состава записывается так:
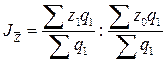
Для выявления влияния на изменение средней величины изменения структуры продукции исчисляют индекс влияния структурных сдвигов.
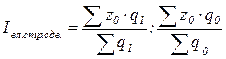 .
.
При этом взаимосвязь между индексами выражается следующей формулой:
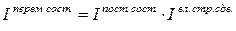 .
.
Расчет индексов постоянного, переменного состава и влияния структурных сдвигов покажем на следующем примере.
Пример 4
Имеются следующие данные о деятельности трех строительных организаций:
| Строительная организация | Средняя заработная плата строительно-монтажных рабочих, ден. ед. | Среднегодовая численность строителей-монтажников, чел. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
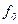
| 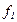
| Т0 | Т1 | |
| «Строй-Сервис» | 1 000 | 1 200 | ||
| «Госстрой» | 1 500 | |||
| «Строймонтаж» | ||||
| ИТОГО | × | × | 2 350 | 3 020 |
Рассчитайте индексы заработной платы переменного и постоянного составов, а также индекс влияния структурных сдвигов.
Объясните результаты расчетов.
Решение:
1. Индекс переменного состава характеризует изменение средней величины качественного показателя – заработной платы – по всей совокупности и рассчитывается по формуле:
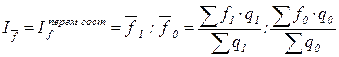 .
.
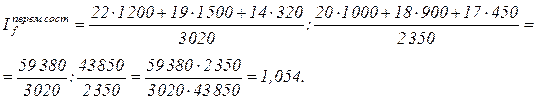
19.66де=ср зар.пл в отч.пер.. 18.66 д.е. ср. зар.пл. в баз пер.
Средняя заработная плата по всем строительным организациям в отчетном периоде по сравнению с базисным увеличилась на 5, 4%. На величину этого индекса оказали влияние два фактора: изменение самой заработной платы и изменение в структуре рабочих.
2. Индекс постоянного состава изучает изменение качественного показателя за счет динамики самого показателя, исключая влияние структурных сдвигов: как видно, в формуле данного индекса коэффициенты при весах q неизменны (фиксируются на уровне отчетного периода):
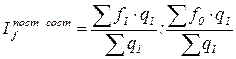 .
.
Рассчитаем индекс заработной платы постоянного состава:
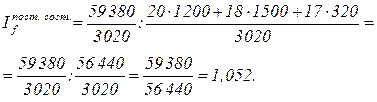
18.69-усл.ср.зар.пл.
Таким образом, средняя заработная плата по всем строительным организациям повысилась на 5, 2% за счет изменения самой заработной платы.
3. Индекс влияния структурных сдвигов характеризует изменение средней величины качественного показателя за счет изменения структуры совокупности и не учитывает влияние динамики самой качественной величины (размер заработной платы фиксируется на уровне базисного периода):
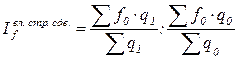 .
.
Рассчитаем, чему равен данный индекс в нашем случае:
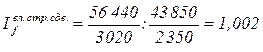 .
.
Таким образом, изменение структуры среднегодовой численности строительно-монтажных рабочих повлекло увеличение средней заработной платы на 0, 2%.
Между индексами переменного и постоянного состава и индексом влияния структурных сдвигов существует взаимосвязь: произведение индекса постоянного состава и индекса влияния структурных сдвигов дает индекс переменного состава.
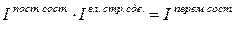 .
.
С помощью взаимосвязи экономических индексов проверим правильность произведенных ранее расчетов:
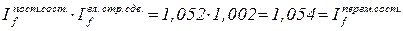
Ответ: средняя заработная плата по трем строительным организациям в отчетном периоде по сравнению с базисным увеличилась на 5, 4%. Данное увеличение на 5, 2% было вызвано динамикой самой заработной платы по всем строительным организациям и на 0, 2% – изменением структры численности строительно-монтажных рабочих данных организаций.
ТЕМА: СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЗАИМОСВЯЗИ