Кручение бруса прямоугольного сечения

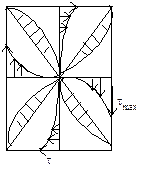При этом нарушается закон плоских сечений, сечения некруглой формы при кручении искривляются – депланация поперечного сечения.

Эпюры касательных напряжений прямоугольного сечения.

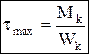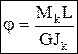; , J_k и W_k — условно называют моментом инерции и моментом сопротивления при кручении. W_k= ahb²,

J_k= bhb³, Максимальные касательные напряжения t_max будут посредине длинной стороны, напряжения по середине короткой стороны: t= g× t_max, коэффициенты: a, b, g приводятся в справочниках в зависимости от отношения h/b (например, при h/b=2, a=0, 246; b=0, 229; g=0, 795.

Изгиб

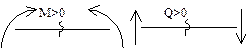Плоский (прямой) изгиб — когда изгибающий момент действует в плоскости, проходящей через одну из главных центральных осей инерции сечения, т.е. все силы лежат в плоскости симметрии балки. Основные гипотезы (допущения): гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения – сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N> 0, если продольная сила растягивающая; при М> 0 волокна сверху балки сжимаются, снизу растягиваются. .

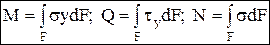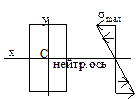Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения: 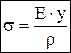, r — радиус кривизны нейтрального слоя, y — расстояние от некоторого волокна до нейтрального слоя. Закон Гука при изгибе: 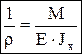, откуда (формула Навье): 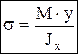, J_x — момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента, EJ_x — жесткость при изгибе, 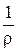— кривизна нейтрального слоя.

Максимальные напряжения при изгибе возникают в точках, наиболее удаленных от нейтрального слоя: 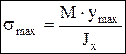, J_x/y_max=W_x—момент сопротивления сечения при изгибе, .

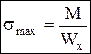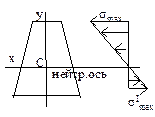Если сечение не имеет горизонтальной оси симметрии, то эпюра нормальных напряжений s не будет симметричной. Нейтральная ось сечения проходит через центр тяжести сечения. Формулы для определения нормального напряжения для чистого изгиба приближенно годятся и когда Q¹ 0. Это случай поперечного изгиба. При поперечном изгибе, кроме изгибающего момента М, действует поперечная сила Q и в сечении возникают не только нормальные s, но и касательные t напряжения. Касательные напряжения определяются формулой Журавского: 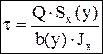, где S_x(y) — статический момент относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии " y" от нейтральной оси; J_x — момент инерции всего поперечного сечения относительно нейтральной оси, b(y) — ширина сечения в слое, на котором определяются касательные напряжения.

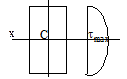Для прямоугольного сечения: 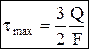, F=b× h, для круглого сечения: 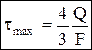, F=p× R², для сечения любой формы ,

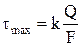k— коэфф., зависящий от формы сечения (прямоугольник: k= 1, 5; круг - k= 1, 33).

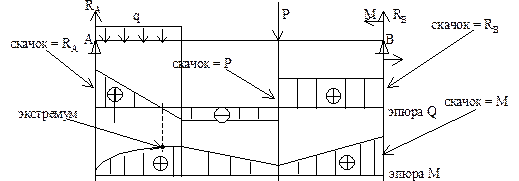M_max и Q_max определяются из эпюр изгибающих моментов и поперечных сил. Для этого балка разрезается на две части и рассматривается одна из них.

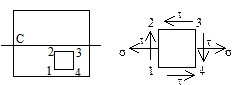Действие отброшенной части заменяется внутренними силовыми факторами М и Q, которые определяются из уравнений равновесия. В некоторых вузах момент М> 0 откладывается вниз, т.е. эпюра моментов строится на растянутых волокнах. При Q= 0 имеем экстремум эпюры моментов. Дифференциальные зависимости между М, Q и q: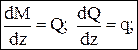

q — интенсивность распределенной нагрузки [кН/м]

Главные напряжения при поперечном изгибе:

.

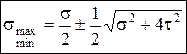Расчет на прочность при изгибе: два условия прочности, относящиеся к различным точкам балки: а) по нормальным напряжениям , (точки наиболее удаленные от С); б) по касательным напряжениям 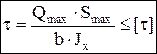, (точки на нейтр.оси). Из а) определяют размеры балки: 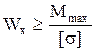, которые проверяют по б). В сечениях балок могут быть точки, где одновременно большие нормальные и большие касательные напряжения. Для этих точек находятся эквивалентные напряжения, которые не должны превышать допустимых. Условия прочности проверяются по различным теориям прочности

I-я: 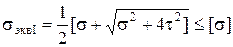; II-я: 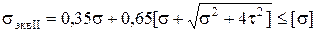(при коэфф.Пуассона m=0, 3); — применяются редко.

III-я: 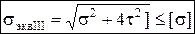, IV-я: ,

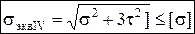теория Мора: 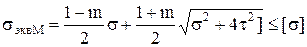, 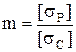(используется для чугуна, у которого допускаемое напряжение на растяжение [s_р]¹ [s_с] – на сжатие).