Статически неопределимые системы

Статически неопределимые системы – системы, силовые факторы в элементах которых не могут быть определены только из уравнений равновесия твердого тела. В таких системах число связей больше, чем необходимо для равновесия. Степень статической неопределимости: S = 3n – m, n – число замкнутых контуров в конструкции, m – число одиночных шарниров (шарнир, соединяющий два стержня, считается за один, соединяющий три стержня – за два и т.д.). Метод сил – в качестве неизвестных принимают силовые факторы. Последовательность расчета: 1) устанавливают степень статич. неопределимости; 2) путем удаления лишних связей заменяют исходную систему статически определимой – основной системой (таких систем может быть несколько, но при удалении лишних связей не должна нарушаться геометрическая неизменяемость конструкции); 3) основную систему загружают заданными силами и лишними неизвестными; 4) неизвестные усилия должны быть подобраны так, чтобы деформации исходной и основной систем не отличались. Т.е. реакции отброшенных связей должны иметь такие значения, при которых перемещения по их направлениям = 0. Канонические уравнения метода сил:

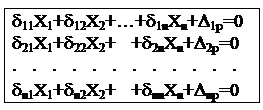Эти уравнения являются дополнительными ур-ями деформаций, которые позволяют раскрыть статич. неопределимость. Число ур-ий = числу отброшенных связей, т.е. степени неопределимости системы.

d_ik – перемещение по направлению i, вызванное единичной силой действующей по направлению k. d_ii – главные, d_ik – побочные перемещения. По теореме о взаимности перемещений: d_ik=d_ki. D_ip– перемещение по направлению связи i, вызванное действием заданной нагрузки (грузовые члены). Перемещения, входящие в канонические уравнения удобно определять по методу Мора.

Для этого к основной системе прикладывают единичные нагрузки Х₁=1, Х₂=1, Х_n=1, внешнюю нагрузку и строят эпюры изгибающих моментов. По интегралу Мора находят: ; ; ….; ;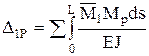

; ; ….; ;

; ; ….; .

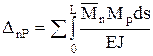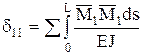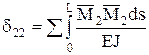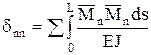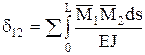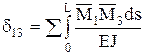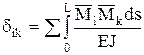Черта над М указывает на то, что эти внутренние усилия вызваны действием единичной силы.

Для систем, состоящих из прямолинейных элементов перемножение эпюр удобно производить по способу Верещагина. ; 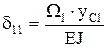и т.д. W_Р – площадь эпюры М_р от внешней нагрузки, y_Ср– ордината эпюры от единичной нагрузки под центром тяжести эпюры М_р, W₁ – площадь эпюры М₁ от единичной нагрузки. Результат перемножения эпюр равен произведению площади одной из эпюр на ординату другой эпюры, взятой под центром тяжести площади первой эпюры.

Расчет плоских кривых брусьев (стержней)

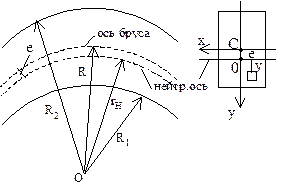К кривым брусьям относятся крюки, звенья цепей, арки и т.п. Ограничения: поперечное сечение имеет ось симметрии, ось бруса плоская кривая, нагрузка действует в той же плоскости. Различают брусья малой кривизны: h/R< 1/5, большой кривизны: h/R³ 1/5. При изгибе брусьев малой кривизны нормальные напряжения рассчитывают по формуле Навье, как для балок с прямой осью: 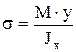. При чистом изгибе брусьев большой кривизны: ,

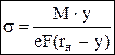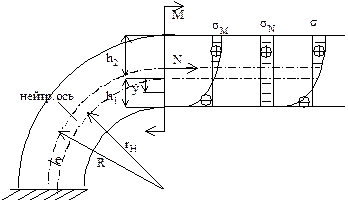r_Н– радиус нейтрального слоя, е=R – r_Н, R – радиус слоя, в котором расположены центры тяжести сечения. Нейтральная ось кривого бруса не проходит через центр тяжести сечения С. Она всегда расположена ближе к центру кривизны, чем центр тяжести сечения. 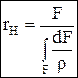, r=r_Н – y. Зная радиус нейтрального слоя можно определить расстояние " е" от нейтрального слоя до центра тяжести. Для прямоугольного сечения высотой h, с наружным радиусом R₂ и внутренним R₁: 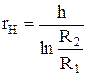; для разных сечений формулы приведены в справочной лит-ре. При h/R< 1/2 независимо от формы сечения можно определять " е" по приближенной формуле: 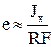, где J_x – момент инерции сечения относительно оси, проходящей через его центр тяжести перпендикулярно плоскости кривизны бруса.

Нормальные напряжения в сечении распределяются по гиперболическому закону (у наружного края сечения меньше, у внутреннего больше). При действии еще и нормальной силы N: 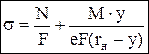(здесь r_Н – радиус нейтрального слоя, который был бы при действии только момента М, т.е. при N=0, но в действительности при наличии продольной силы этот слой уже не является нейтральным). Условие прочности: 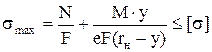, при этом рассматриваются крайние точки, в которых суммарные напряжения от изгиба и растяжения–сжатия будут наибольшие, т.е. y= – h₂ или y= h₁. Перемещения удобно определять методом Мора.