Задача к билету № 11

Какую жёсткость имеет пружина, на которой шарик массой 150 г совершает 250 колебаний за 2, 5 мин?

m=150 г = 0, 15 кг;

n = 250;

t = 2, 5 мин = 150 c.

Изобразим рисунок условия задачи:

Запишем формулу периода колебания пружины:

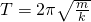
Выразим жесткость пружины:

к= (2π)²•m/Т².

Выразим период колебания пружины Т через частоту колебаний ν =n/t:

Т = 1/ν = t/n.

Находим формулу для жёсткости и выполним вычисления:

к = (2π)²•m/Т² = (2π)²•m•(n/t)² = (2π)²•0, 15•(250/150)² ≈ 16, 43 Н/м.

Ответ:

жёсткость пружины составляет 16, 43 Н/м.

Задача к билету № 12

Идеальный газ нагревают от 300 К до 750 К при постоянном давлении, в результате чего его объём увеличивается на 6 л. Определите начальный объём газа.

Р=const;

Δ V=6 л=6•10^-3 м³;

Т1=300 К;

Т2=750 К.

Применим уравнение Клапейрона, с учетом того, что Р=const, имеем:

V1/T1=V2/T2,

где V1 – начальный объём газа;

V2 – конечный объём газа.

Выразим конечный объём газа через начальный объём газа как V2=V1+Δ V,

где Δ V – заданное в задаче изменение объёма после нагрева газа,

и подставляем в уравнение Клапейрона:

V1/T1=(V1+Δ V)/T2.

Отсюда:

V1•T2 = (V1+Δ V)•T1 = V1•T1+Δ V•T1;

V1•(T2-T1) = Δ V•T1;

V1 = (Δ V•T1)/(T2-T1) = (6•10^-3•300)/(750-300) = 1, 8/450=4•10^-3 м³.

Ответ:

начальный объём газа составляет 4 литра.