Сила Ампера;

2) сила ваги провідника.

Сила Ампера Fа, діюча на провідник зі струмом, який поміщений в магнітне поле, залежить від (дивись рисунок):

а) величини магнітної індукції В;

б) величини струму I в провіднику;

в) активної довжини провідника L;

г) синуса кута α між вектором магнітної індукції і напрямом струму в провіднику.

Загальна формула сили Ампера:

Fа=B•І•L•sin α.

Напрям дії сили Ампера визначається за правилом лівої руки (дивись рисунок).

У зв’язку з тим, що за умовами задачі провідник висить в однорідному полі нерухомо, кут α рівний 90⁰ (sin α =1).

Сила ваги провідника має наступну загальну формулу: Fв=m•g.

Запишемо рівняння, яке визначає умову задачі: Fв= Fа.

Звідси: m•g = B•І•L.

Індукцію магнітного поля визначаємо за формулою:

В=(m•g)/I•L=(0, 2•10)/20•2=0, 05 Тл.

Відповідь:

індукція магнітного поля складає 0, 05 Тл.

Задача до білета № 23

Протон рухається в однорідному магнітному полі у вакуумі по колу радіусом 1 см. Визначте швидкість руху протона, якщо індукція магнітного поля становить 0, 2 Тл.

R=1 см=10^-2 м;

В=0, 2 Тл.

Намалюємо рисунок відповідно умовам задачі:

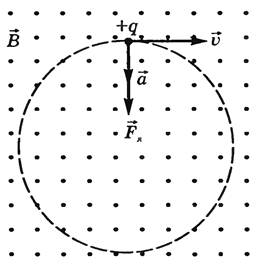
На протон, при русі по колу, діють дві сили, які врівноважують одна іншу:

1) сила Лоренца – є доцентровою силою і визначається як Fл=q•V•B•sin α,

де q – заряд протону, який дорівнює 1, 6•10^-19 Кл;

V – швидкість протону (напрям вектора швидкості завжди по дотичній до кола);

B – індукція магнітного поля, у якому знаходиться протон;

α – кут між вектором швидкості заряду (в нашому випадку – частинки) і вектором магнітної індукції, який в цьому випадку дорівнює 90⁰;

2) відцентрова сила, яка визначається як Fв=(m•V²)/R,

де m – маса протону, яка приблизно дорівнює 1, 67·10^{− 27} кг;

V – швидкість протону;

R – радіус кола.

Запишемо відповідне рівняння: Fл= Fв. Звідси:

q•V•B=(m•V²)/R або q•B=(m•V)/R.

Тепер визначити швидкість руху протона:

V=(q•B•R)/m=1, 6•10^-19•0, 2•10^-2/1, 67·10^{− 27} ≈ 2•10⁵ м/c.

Відповідь:

швидкість руху протона складає 2•10⁵ м/c.

Задача до білета № 24

На клеми котушки опором 8 Ом з індуктивністю 25 мГн подається напруга 56 В. Яка енергія виділиться в процесі розмикання ланцюга?

R=8 Ом;

L=25 мГн=25·10^–3 Гн;

U=56 В.

Енергія магнітного поля котушки зі струмом визначається формулою:

W=L•I²/2.

За законом Ома струм визначається як: I=U/R.

Звідси: W= L•(U/R)²/2 = 25·10^–3•(56/8)²/2 = 0, 6125 Дж.

Відповідь:

в процесі розмикання ланцюга виділиться 0, 6125 Дж енергії.

Задача до білета № 25

Коливальний контур складається з конденсатора ємністю 400 пФ і котушки з індуктивністю 10 мГн. Визначте амплітудну напругу на обкладках конденсатора, якщо амплітуда сили струму в контурі 0, 1 А.

С=400 пФ=4 • 10^–10 Ф;

L=10 мГн=10^–2 Гн;

I_max=0, 1 А=10^–1 А.

Розглянемо рисунок:

Коливальним контуром називають електричне коло, складене із конденсатора та котушки індуктивності. У такому колі енергія електричного поля конденсатора може перетворюватись в енергію магнітного поля котушки. Одночасні зміни взаємозв’язаних між собою електричного і магнітного полів називаються електромагнітними коливаннями.

Щоб одержати електромагнітні коливання необхідно зарядити конденсатор та замкнути електричне коло (дивись рисунок).

В момент часу t=0 (дивись рисунок), якщо конденсатор має електричну ємність С, а зарядили його до напруги U, то між його обкладками наведеться електричне поле Е=max з енергією W_C=С • U²_max/2, а в цей час у котушці індуктивності магнітне поле індукції буде В=0.

При замиканні ключа К конденсатор почне розряджатись через котушку індуктивності, але розряд не буде миттєвим, оскільки при з'єднанні конденсатора з котушкою індуктивності, в ланцюзі потече струм, що викличе в котушці індуктивності електрорушійну силу (ЕРС) самоіндукції, спрямовану на зменшення струму (протидіятиме наростанню струму) в ланцюзі.

Через деякий час t конденсатор повністю розрядиться, а в котушці індуктивності буде наведене магнітне поле максимальної індукції В=max з енергією W_L=L • I²_max/2, а в цей час у конденсаторі електричне поле стане Е=0. Якщо вважати, що енергія не втрачається на випромінювання та нагрівання провідників, тоді W_C=W_L.

З урахуванням того, що максимальна енергія, що накопичується на ємності, дорівнює максимальній енергії, що накопичується на індуктивності після розряду конденсатора, можна записати: W_C=W_L. Використовуючи формули для W_C і W_L запишемо наступне рівняння: С • U²/2=L • I²_max/2. Звідси вираховуємо значення амплітудної напруги на обкладках конденсатора:

U²= L • I²_max/С =10^–2 • 10^–2/4 • 10^–10 = 0, 25 • 10⁶;

U=0, 5 • 10³=500 В.

Відповідь:

амплітудна напруга на обкладках конденсатора становить 500 В.

Задача до білета № 26

На яку довжину хвилі налаштований радіоприймач, якщо його коливальний контур має індуктивність 2 мГн і ємність 2 нФ?

L = 2 мГн = 2·10^–3 Гн;

С = 2 нф = 2·10^–9 Ф.

Згідно з формулою Томсона період коливального контуру:

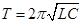
Довжина хвилі пов’язана з період коливального контуру:

,

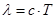де с – швидкість електромагнітної хвилі, яка дорівнює 3•10⁸ м/с.

Звідси знаходимо:

λ =3•10⁸•2π •(2·10^–3•2·10^–9)^1/2=18, 84•10⁸•2•10^–6=37, 68•10²=3768 м

Відповідь:

довжина хвилі становить 3768 м.

Задача до білета № 27

При якому куті падіння променя з повітря на скло кут заломлення в два рази менше від кута падіння?

α /β = 2.

n1 – показник заломлення повітря, який дорівнює 1;

n2 – показник заломлення скла, який дорівнює 1, 5.

Намалюємо рисунок відповідно умовам задачі:

Скористаємося законом Снеліуса, який записується як:

sin α /sin β = n2/n1,

де α – кут падіння;

β – кут заломлення.

Визначимо кут заломлення через кут падіння: β =α /2.

Запишемо закон Снеліуса наступним чином:

sin α /sin (α /2) = 1, 5.

Звідси потрібно вирішити рівняння: sin α –1, 5•sin (α /2) = 0.

2•sin (α /2)•cos (α /2)–1, 5•sin (α /2) = 0 або 2•cos (α /2)–1, 5 = 0 або cos (α /2)=0, 75.

Далі: α /2 = arcos 0, 75 і α =2•arcos 0, 75.

Відповідь:

кут падіння становить α =2•arcos 0, 75.

Задача до білета № 28

Знайдіть довжину хвилі електромагнітного випромінювання, енергія кванта якого дорівнює енергії спокою електрона.

m_e – маса спокою електрона, яка дорівнює 9, 1•10^-31 кг.

Енергія спокою електрона визначається за формулою Ейнштейна:

Е_е = m_e•с²,

де с – швидкість світла, яка дорівнює 3•10⁸ м/с;

Енергія кванта електромагнітного випромінювання фіксована і дорівнює:

E_к = h•ν,

де h – постійна Планка, яка дорівнює 6·10^-34Дж·с;

ν – частота електромагнітного випромінювання.

Частоту електромагнітного випромінювання можна визначити через довжину хвилі електромагнітного випромінювання: ν =с/λ,

де с – швидкість світла;

λ - довжина хвилі електромагнітного випромінювання.

За умовами задачі Е_е = E_к. Звідси: m_e•с² = h•(с/λ).

Знаходимо довжину хвилі електромагнітного випромінювання:

λ = h/(m_e•с) = 6·10^-34/(9, 1•10^-31•3•10⁸) ≈ 2, 2•10^-12 м.

Відповідь:

довжина хвилі електромагнітного випромінювання становить 2, 2•10^-12 м.

Задача до білета № 29

Поверхня нікелю освітлюється світлом з довжиною хвилі 200 нм. Знайдіть червону межу фотоефекту, якщо максимальна швидкість фотоелектронів
6, 5× 10⁵ м/с.

λ =200 нм=2•10^-7 м;

V=6, 5•10⁵ м/с.

Червона межа фотоефекту (це максимальна довжина хвилі λ _max світла або мінімальна частота ν _min, при яких ще можливий зовнішній фотоефект) визначається за формулами:

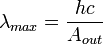
і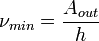

де 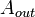– робота виходу для конкретного фотокатода;

h – постійна Планка, яка дорівнює 6·10^-34Дж·с;

с – швидкість світла, яка дорівнює 3•10⁸ м/с.

Для кожної речовини існує власна червона межа фотоефекту (поріг фотоефекту) – така найбільша довжина світлової хвилі λ _max (чи найменша частота ν _min), за якої ще можливий фотоефект (якщо ν £ ν _min чи λ ³ λ _max, то фотоефект не існує).

Визначення:

а) фотоефект – явище «вибивання» світлом електронів із металів. Це повне або часткове вивільнення електронів від зв'язків з ядрами атомів речовини внаслідок дії на неї електромагнітного проміння (світла, рентгенівського чи гамма-променів);

б) зовнішній фотоефект – вибивання електронів під дією світла (фотоелектронна емісія):

в) робота виходу електрона – це найменша кількість енергії, яку необхідно надати електрону для того, щоб вивести його з твердого тіла у вакуум;

г) фотокатод – негативно заряджений електрод (катод) в світлочутливих пристроях, що працюють з використанням зовнішнього фотоефекту. Фотокатоди виготовляються з електропровідних світлочутливих сполук. Коли на фотокатод потрапляє квант світла (фотон), поглинена енергія викликає емісію електронів за рахунок зовнішнього фотоефекту;

д) фотоэлектрон – электрон, выделившийся из атома вещества под воздействием световой энергии;

е) зазвичай роботу виходу заведено вимірювати в електронвольтах (еВ).

Визначимо спочатку енергію фотону, відповідного заданим довжинам світлових хвиль. Енергія фотона обчислюється за формулою: Е = h•(c/λ),

де c/λ – частота світла.

Енергія фотона витрачається:

1) на здійснення роботи виходу електрона з металу;

2) на надання електрону кінетичної енергії.

Складаємо рівняння Ейнштейна для зовнішнього фотоефекту (виражає закон збереження енергії): Е = A + T,

де A – робота виходу електрона з металу;

T – кінетична енергія фотоелектрона.

Робота виходу електрона з металу визначимо як A=(h•c)/λ _max,

де h – постійна Планка, яка дорівнює 6·10^-34 Дж·с.

Кінетична енергія електрона дорівнює T=(m_e•V²)/2,

де m_e – маса спокою електрона, яка дорівнює 9, 1•10^–31 кг.

Запишемо рівняння: (h•c)/λ =(h•c)/λ _max+(m_e•V²)/2. З цієї формули визначаємо червону межу фотоефекту:

λ _max = (h•c)/[(h•c)/λ –(m_e•V²)/2] =

=[(6•10^–34)•(3•10⁸)]/{[(6•10^–34)•(3•10⁸)]/2•10^–7}–{[9, 1•10^–31)•(6, 5•10⁵)²]/2}≈ 2, 5•10^–7 м.

Виконаємо перевірку отриманого результату з умовами задачі: λ _max> λ. Висновок: червона межа фотоефекту знайдена вірно.

Відповідь:

≈ 2, 5•10^–7 м.

Це може бути цікаво:

за отриманим результатом вирахуємо роботу виходу електрона з нікелю і зрівняємо її значення з довідником (А_НІКЕЛЯ=4, 5 еВ).

A=(h•c)/λ _max, = (6•10^-34)•(3•10⁸)/(2, 5•10^–7)=7, 2•10^–19 Дж.

Скористаємось довідниковим співвідношенням: 1 еВ=1, 6•10^–19 Дж.

A=(7, 2•10^–19)/(1, 6•10^–19)=4, 5 еВ.

Що і потрібно було довести́!

Задача до білета № 30

Скільки льоду, узятого при температурі -10 °С, можна перетворити на пару за рахунок енергії, що виділяється при діленні 8 г урану-235?

m = 8 г = 8·10^-3 кг;

t=-10 °С;

n=235 г/моль=235·10^-3 кг/моль - молярна маса урану-235;

N_А=6, 02·10²³ моль - число Авогадро.

Енергія, що виділяється при діленні N-ої кількості ядер урану–235 вираховується за формулою:

Е=Е₀•N,

де E₀ – кількість енергії, що виділяється при діленні одного ядра урану–235, яка дорівнює 200 МэВ (дані з довідника) або 200•10⁶ эВ

або 200•10⁶•(1, 6•10^-19)=320•10^-13 Дж;

N – кількість атомів у m грамах урану–235.

Визначаємо кількість атомів у 8 грамах урану–235:

N=v•N_А,

де v – кількість речовини, формула якої: v=m/n.

Звідси: N= (m/n)•N_А.

Визначаємо кількість енергії, що виділяється при діленні 8 г урану–235:

Ед=Е₀•N= Е₀•(m/n)•N_А= (320•10^-13)•(8•10^-3/235•10^-3)•6, 02•10²³ = 65, 58•10¹⁰ Дж.

Для того, щоб перетворити визначену кількість льоду на пару необхідно:

1) нагріти лід до точки плавлення (t₁=0 °С);

2) розплавити лід, тобто перетворити лід на воду;

3) нагріти воду до точки кипіння (t₂=100 °С);

4) нагріти воду до стану випаровування.

Енергія, яка потрібна для нагрівання льоду до точки плавлення, становить:

Е_н=c_л•m•(t₁–t),

де c_л=2, 1•10³ Дж/(кг•°С) – питома теплоємність льоду;

m – маса льоду.

Енергія, яка потрібна для розплавлення льоду, становить:

Е_п=L_л•m,

де L_л=335•10³ Дж/кг – питома теплота плавлення льоду;

m – маса льоду.

Енергія, яка потрібна для нагрівання води до стану кипіння:

Е_к=c_в•m•(t₂–t₁),

де c_в=4, 2•10³ Дж/(кг•°С) – питома теплоємність води;

m – маса води.

Енергія, яка потрібна для випаровування води:

Е_в=L_в•m,

де L_в=2260•10³ Дж/кг – питома теплота випаровування води;

m – маса води.

Визначаємо повну кількість енергії, яка необхідна для перетворення льоду на пару: Ел=Е_н + Е_п + Е_к + Е_в.

Ел=c_л•m•(t₁–t)+L_л•m+c_в•m•(t₂–t₁)+L_в•m=m•[c_л•(t₁–t) + L_л + c_в•(t₂–t₁) + L_в] =

= m•[2, 1•10³•(0-(-10) + 335•10³ + 4, 2•10³•(100-0) + 2260•10³] =

= m•10³•(21+335+420+2260)= m•3036•10³ Дж.

З урахуванням того, що вся енергія Ед, яка виділяється при діленні 8 г урану–235, йде на випаровування льоду, запишемо рівняння: Ед=Ел. Звідси:

65, 58•10¹⁰ = m•3036•10³.

Знаходимо масу льоду:

m = (65, 58•10¹⁰)/(3036•10³) ≈ 0, 0216•10⁷ ≈ 216000 кг.

Відповідь: