функциясының нүктесіндегі - бойынша алынған дербес өсімшесін тап

A)

$$$ 460

Функциясының нү ктесіндегі градиентін тап

A) (5; -1)

$$$ 461

Нү ктесі кем дегенде екі рет дифференциалданатын функциясының максимум нү ктесі болу ү шін қ андай шарт орындалады

A)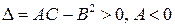

$$$ 462

Нү ктесі кем дегенде екі рет дифференциалданатын функциясының минимум нү ктесі болу ү шін қ андай шарт орындалады

A)

$$$ 463

Функциясы экстремум немесе стационар нү ктелерінде қ андай шартты қ анағ аттандырады

A)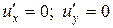

$$$ 464

Функциясының - дербес туындысын тап

A)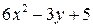

$$$ 465

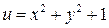функциясының 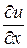- дербес туындысының 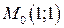нү ктесіндегі мә нін тап:

A) 2

$$$ 466

Функциясының экстремум нү ктелерін тап

A) (2, -2) –максимум нү ктесі

$$$ 467

Функциясын экстремумге зерттең із

A) экстремумы жоқ

$$$ 468

Функциясын экстремумге зерттең із

A)

$$$ 469

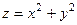функциясы берілген. Табың ыз :

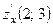A) 4

$$$ 470

Функциясының нү ктесінде векторының бағ ыты бойынша алынғ ан туындысын тап

A) 0

$$$ 471

Функциясының нү ктесінде векторының бағ ыты бойынша алынғ ан туындысын тап

A) 0

$$$ 472

Z=x²+y²-2x -2y +6 ^{функциясының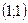} нү ктесінде 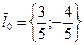векторының бағ ыты бойынша алынғ ан туындысын тап

A) 0

Кем дегенде екі рет диффенренциалданатын z=f(x, y) функциясының x₀, y₀ нү ктесінде экстремум болмауының шартын кө рсету керек

∆ =AC-B²< 0

$$$ 474

Z=x²+y²-2x-2y+3функциясының экстремум нү ктелерін тап (1, 1)- min нү ктесі

$$$ 475

Z=3x²-2x√ y +y-8x+8 функциясының экстремум нү ктелерін жә не сол нү ктедегі функцияның мә нін тап

M(2, 4) мин. Нү ктедегі z(min)=0