Определение момента инерции тракторного шатуна

Момент инерции тела относительно данной оси выражает меру инерции тела при вращательном движении и измеряется суммой произведений масс точек тела на квадраты их расстояний до оси:

.

Для тел правильной геометрической формы (шар, диск, стержень и т. д.) момент инерции можно вычислить методами интегрального исчисления. Но во многих случаях момент инерции оказывается возможным найти лишь опытным путём.

Цель работы состоит в определении момента инерции тракторного шатуна по результатам измерений периода его колебаний в поле силы тяжести (физический маятник).

Маятником называют тело способное колебаться в поле силы тяжести. Различают 3 вида маятников: пружинный, математический и физический.

Пружинным маятником называют тело массой подвешенное на невесомой пружине жесткостью 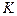. Если сместить его от положения равновесия в вертикальной плоскости и отпустить, то оно будет колебаться вблизи положения равновесия с циклической частотой 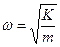и периодом 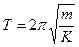(подробнее о пружинном маятнике см. лаб. раб. № 7).

Математический маятник представляет собой тело, являющееся материальной точкой, закрепленное на невесомом нерастяжимом подвесе. Если тело отклонить от положения равновесия в вертикальной плоскости на небольшой угол и отпустить, то оно будет колебаться вблизи положения равновесия с циклической частотой 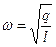и периодом 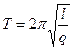. В этих формулах 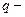ускорение свободного падения, а длина подвеса.

Физическим маятником называют любое реальное тело, закрепленное на горизонтальной оси, не проходящей через центр инерции. Колебания его вокруг оси подобны колебаниям математического маятника и совершаются с циклической частотой 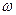и периодом 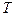, значения, которых, находятся по формулам:

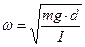(1),

(2),

где 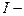момент инерции относительно оси подвеса; 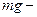сила тяжести; расстояние от оси, относительно которой совершаются колебания, до центра тяжести.

Из формулы (2) следует, что, зная период колебаний тела можно найти момент инерции относительно оси по формуле:

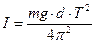(3).

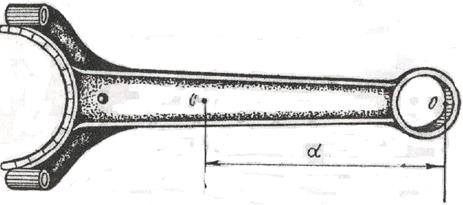
Если в качестве физического маятника используется тракторный шатун, то из этой формулы следует, что для расчета его момента инерции необходимо найти массу тракторного шатуна, определить положение его центра тяжести, измерить период колебаний и расстояние 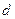от центра тяжести до оси подвеса (черт. 1).

Зная момент инерции тракторного шатуна относительно оси подвеса 0, можно определить и момент инерции 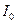тракторного шатуна относительно параллельной оси, проходящей через центр тяжести С. Для этого используют теорему Штейнера (см. лаб. раб. 3). Согласно этой теореме

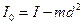. (4)

В этой формуле: 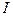- момент инерции тракторного шатуна относительно оси подвеса, 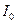- момент инерции шатуна относительно оси, проходящей через центр тяжести шатуна параллельно оси подвеса, 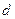- расстояние между осями, равное длине отрезка ОС.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Взвешиванием на весах определить массу тракторного шатуна.

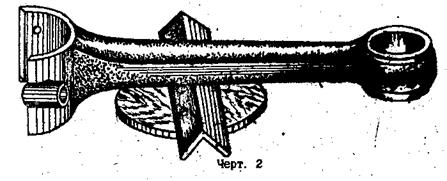
2.Найти центр тяжести тракторного шатуна. Для чего положить шатун на острую подставку и добиться его равновесия (черт. 2). Точка опоры соответствует положению центра тяжести.

3.Измерить расстояние 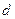между центром тяжести шатуна и осью подвеса (отрезок ОС на черт. 1) и занести его в таблицу.

4.Найти период колебаний тракторного шатуна. Для чего подвесить его на трехгранной призме и, отклонив на небольшой угол от положения равновесия, отпустить, одновременно включив секундомер. Измерить время 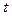50-ти полных колебаний.

5.Повторить измерения времени 50-ти полных колебаний шатуна еще два раза и все результаты измерений занести в таблицу. Рассчитать среднее время 50-ти полных колебаний.

Таблица 1

	Численное значение	Абсолютная погрешность	Относительная погрешность
Сила тяжести тракторного шатуна mg (Н)
Масса тракторного шатуна m (кг)
Расстояние от оси подвеса до центра тяжести (м)
Время 50 колебаний (с)	t1
t2
t3
tср
Период колебаний Т (с)
Момент инерции относительно оси подвеса I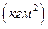
Момент инерции относительно оси, проходящей через центр тяжести параллельно оси подвеса I0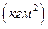

6.Найти среднее значение периода колебаний шатуна по формуле 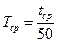. По формулам (3), (4) вычислить момент инерции шатуна относительно оси подвеса и оси, проходящей через центр инерции, результаты вычислений занести в таблицу.

7.Оценить относительные и абсолютные погрешности результатов определения моментов инерции шатуна относительно оси подвеса, и относительно оси, проходящей через центр инерции по формулам (4), (5).

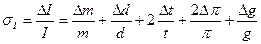(5)

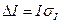
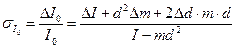(6)

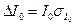
Для получения зачёта по данной работе необходимо проработать следующие вопросы.

1. Величины, характеризующие колебательное движение (смещение, амплитуда, фаза, период, частота).

2. Скорость и ускорение в колебательном движении.

3. Упругая и квазиупругая сила.

4. Энергия колебательного движения.

5. Период собственных свободных упругих колебаний.

6. Математический и физический маятник. Приведённая длина физического маятника.

Контрольная задача.

Стержень длиной в 1 м. и весом 3 кг. Колеблется около оси, перпендикулярной его длине и проходящей через его конец.

Определить период колебаний. Как изменится период колебаний, если на свободном конце стержня укрепить груз массой 800 г. (груз считать за материальную точку).

Л и т е р а т у р а

1. Савельев И.В. Курс общей физики, т.1. Механика. Колебания и волны. Молекулярная физика, изд. 5, стр. 141-145, 196-199, М., «Наука», 1977.

2. Стрелков С.П. Общий курс физики т.1. Механика, изд. 3 переработанное, стр. 211-215, 421-428, М., «Наука», 1975.