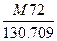Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
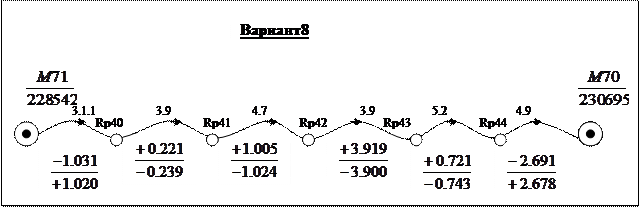
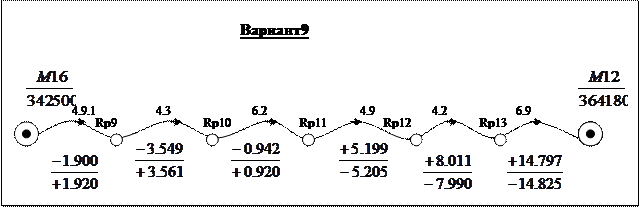
Уравнивание одиночного нивелирного хода
|
|
| № секции | № марок и реперов | Длины секций L, км | Превышения | Расхождения | d2 | d2 L | Поправки n, мм | Исправленные превышения h+n, м | Отметки H, м | Вес отметки PH | Ср. кв. ошибка МH, мм | Ср. кв. ошибка самой ошибки mМH, мм | ||||
| Прямой ход h, м | Обратный ход h, м | Среднее h, м | Полученные d, мм | Предельно допустимые, мм | ||||||||||||
| М25 | 3, 1 | +3, 617 | -3, 627 | +3, 622 | -10 | +4 | +3, 626 | 151, 635 | ||||||||
| Рп11 | 155, 261 | 0, 39 | 4, 2 | 1, 31 | ||||||||||||
| 4, 2 | +5, 169 | -5, 178 | +5, 174 | -9 | +6 | +5, 180 | ||||||||||
| Рп12 | 160, 441 | 0, 22 | 5, 5 | 1, 75 | ||||||||||||
| 3, 9 | -5, 343 | +5, 349 | -5, 346 | +6 | +5 | -5, 341 | ||||||||||
| Рп13 | 155, 100 | 0, 22 | 5, 5 | 1, 75 | ||||||||||||
| 1, 7 | +9, 659 | -9, 663 | +9, 661 | -4 | +3 | +9, 664 | ||||||||||
| Рп14 | 164, 764 | 0, 25 | 5, 2 | 1, 64 | ||||||||||||
| 5, 9 | -8, 246 | +8, 265 | -8, 256 | +19 | +8 | -8, 246 | ||||||||||
| М27 | 156, 516 | |||||||||||||||
| 18, 8 | +4, 856 | -4, 854 | +4, 855 | +26 | ||||||||||||
НК – НН = +4, 881 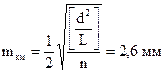
fh = -0, 026 м контроль 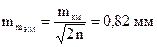
fh пред. = 0, 043 м 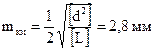
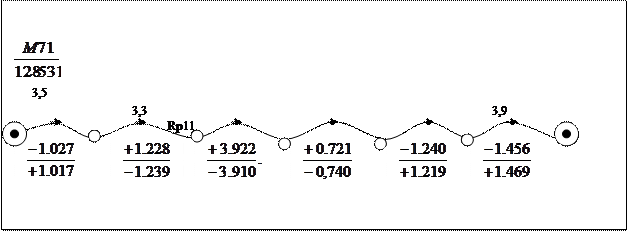
Данные для решения задачи
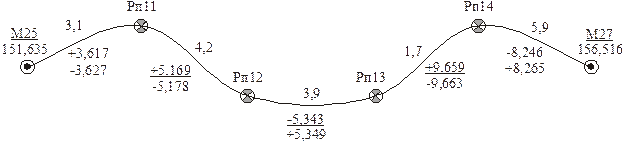
Рис. 4.
В графы 1, 2, 3, 4 и 5 выписывают исходные данные и измеренные величины со схематического чертежа (рис. 4). Дальнейшие вычисления выполняют в следующей последовательности:
1. В графе 6 вычисляют средние превышения по секциям. Знак берут по прямому ходу, а величину – как среднее арифметическое из абсолютных значений hпр и hобр.
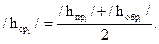 (1)
(1)
2. Контроль вычислений средних превышений выполняют суммированием величин, записанных в графы 4, 5 и 6 по формуле
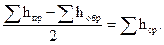 (2)
(2)
3. В графе 7 вычисляют расхождения di (в мм) между превышениями прямого и обратного ходов
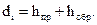 (3)
(3)
4. Полученные разности сравнивают с предельными значениями (графа 8), найденными по формуле
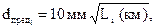 (4)
(4)
где Li – длина секции в км.
5. Для оценки точности полевых измерений в графах 9 и 10 вычисляют величины d2 и d2/L, причём величины d берут в мм, а L – в км. После этого вычисляют среднюю квадратическую ошибку среднего превышения на 1 км хода по формулам:
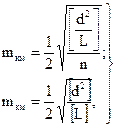 (5)
(5)
где d – разность между hпр и hобр в секции, мм;
L – длина секции, км;
[L] – длина хода, км.
6. Ошибка самой ошибки характеризует точность получения величины mкм, вычисляемой по формуле
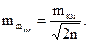 (6)
(6)
7. Посчитывают невязку по ходу
 (7)
(7)
где 
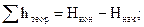
Нкон и Ннач – отметки конечной и начальной марок или реперов.
8. Полученную невязку по формуле 7 сравнивают с предельной невязкой нивелирного хода
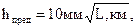 (8)
(8)
где L – длина хода в км.
9. Делают вывод о качестве (точности) полевых измерений. Если:
- di £ dпред;
- mкм £ 5 мм (допуск по инструкции для III кл.);
- fh £ fh доп,
то измеренные превышения по точности соответствуют III классу. В противном случае превышения перемеряют в поле.
10. Полученную невязку fh распределяют с обратным знаком пропорционально длинам секций хода, т.е. вычисляют в графе 11 поправки vi по формуле
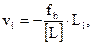 (9)
(9)
где [L] – длина хода, км;
Li – длина секции, км.
(Поправки вычисляют в мм, следовательно fh берут в мм.)
11. Контроль вычисления поправок проверяют по формуле
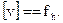 (10)
(10)
12. Уравненные превышения вычисляют в графе 12
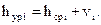 (11)
(11)
13. Уравненные отметки находят в графе 13 по формуле
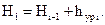 (12)
(12)
Если уравнивание выполнено верно, то
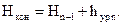 (13)
(13)
14. Веса уравненных отметок промежуточных реперов определяют по формуле
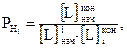 (14)
(14)
где 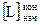 – длина всего хода, км;
– длина всего хода, км;
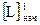 – длина хода от начальной марки до репера с номером i, км;
– длина хода от начальной марки до репера с номером i, км;
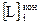 – длина хода от репера i до конечной марки с номером, км.
– длина хода от репера i до конечной марки с номером, км.
15. Среднюю квадратическую ошибку уравненных отметок вычисляют по формуле
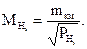 (15)
(15)
16. Ошибки самих ошибок находят по формуле
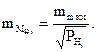 (16)
(16)
17. Из всех MH i выбирают самую большую
max MH i = MH слаб,
где MH слаб – ошибка в слабом месте (примерно в середине хода).
Должно выполняться условие
MH слаб £ Dпред,
где Dпред – предельная СКО положения точки по высоте в середине хода после уравнивания.
Dпред = М,
где М – СКО положения по высоте конечной точки хода до уравнивания.
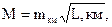
где L, км – [L] – длина хода.
Если max MH i £ 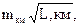 то уравненные отметки соответствуют по точности III классу.
то уравненные отметки соответствуют по точности III классу.
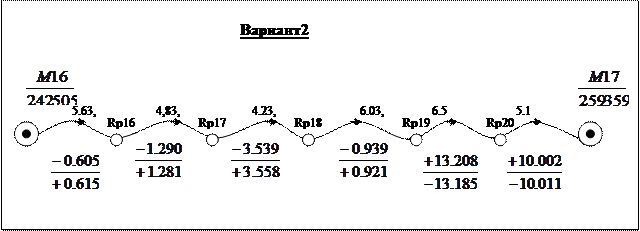
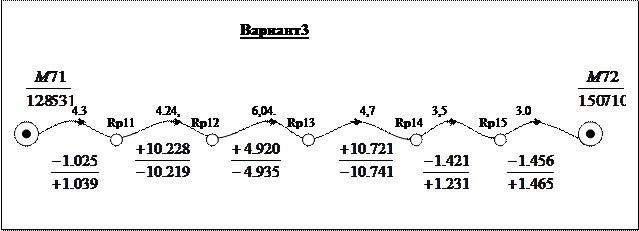
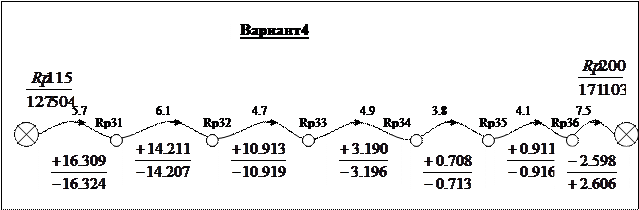
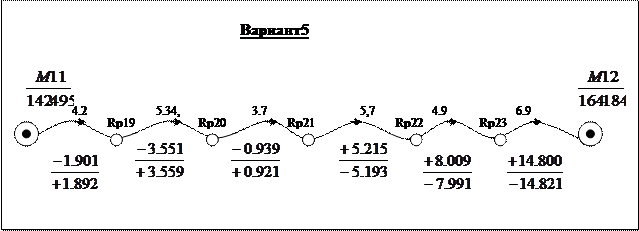
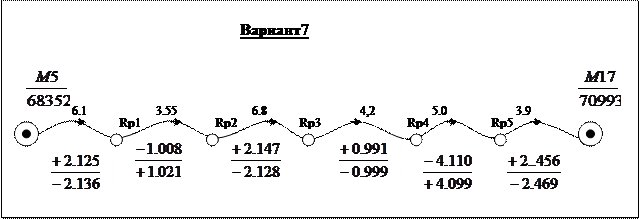
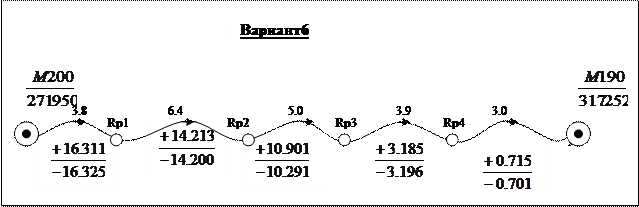
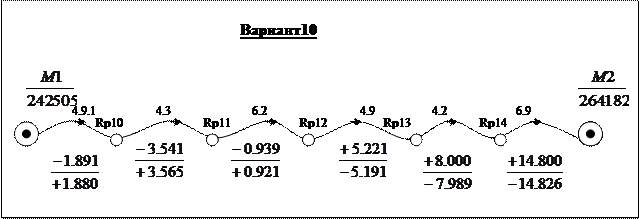
Всего подготовлено 10 вариантов каждого задания; по одному варианту на студента. Номер варианта N определяется единицами e индивидуального шифра студента. Например: шифр 99124, e=4, номер варианта N=4; шифр 00100, e=0, номер варианта N=10.
Варианты к контрольной работе №3
| |||||||
| |||||||
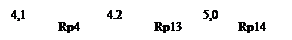 | |||||||
| |||||||