Случайные переменные

Пусть случайная переменная Х(А) представляет функциональное отношение между случайным событием А и действительным числом. Для удобства записи обозначим случайную переменную через X, а ее функциональную зависимость от А будем считать явной. Случайная переменная может быть дискретной или непрерывной. Функция распределения F_x(х) случайной переменной X описывается выражением

F_x(x)=P(X≤ x), (4.4)

где Р(Х ≤ х) — вероятность того, что значение, принимаемое случайной переменной X, меньше действительного числа х или равно ему. Функция распределения F_x(x) имеет следующие свойства:

1.0 ≤ F_x(x) ≤ 1

2. F_x(x₁) ≤ F_x(x₂), если x₁ ≤ x₂

3. F_x( − ∞ ) = 0

4. F_x( +∞ ) = 1

Еще одной полезной функцией, связанной со случайной переменной X, является плотность вероятности, которая записывается следующим образом:

. (4.5, а)

Как и в случае функции распределения, плотность вероятности — это функция действительного числа х. Название " функция плотности" появилось вследствие того, что вероятность события x ₁ ≤ X ≤ x ₂ равна следующему:

P (x ₁ ≤ X ≤ x ₂) = P (X ≤ x ₂) – P (X ≤ x ₁) = (4.5, б)

= F_x(x ₂ ) – F_x(x ₁ ) =

.

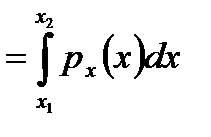Используя уравнение (4.5, 6), можно приближенно записать вероятность того, что случайная переменная X имеет значение, принадлежащее очень узкому промежутку между х и х + Δ x:

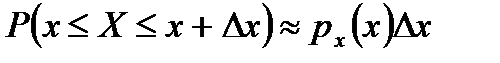. (4.5, в)

Таким образом, в пределе при Δ x, стремящемся к нулю, мы можем записать следующее:

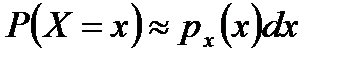. (4.5, г)

Плотность вероятности имеет следующие свойства:

1. p_x(х) ≥ 0

2.

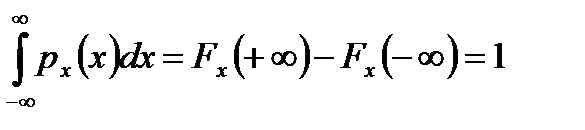
Таким образом, плотность вероятности всегда неотрицательна и имеет единичную площадь. В тексте книги мы будем использовать запись р_х(х) для обозначения плотно­сти вероятности непрерывной случайной переменной. Для удобства записи мы часто будем опускать индекс X и писать просто р(х). Если случайная переменная X может принимать только дискретные значения, для обозначения плотности вероятности мы будем использовать запись р(Х=х_i).

Основная литература 2 [38-50]; 6 [56-59].

Дополнительная литература 4[ 124-135], 5[ 266-277].

Контрольные вопросы:

1. Что такое автокорреляция;

2. Автокорреляция перидического сигнала;

3. Случайные сигналы дайте определение.

Лекция №5 (1 час.)