
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основні теоретичні відомості та методичні поради. Успадковування - це процес передачі спадкових особливостей організму від одного покоління до іншого.
|
|
Успадковування - це процес передачі спадкових особливостей організму від одного покоління до іншого.
Закономірності успадковування ознак вивчаються за допомогою генетичного аналізу, тобто сукупності генетичних методів. Головний елемент генетичного аналізу – гібридологічний метод, або метод схрещування. Цей метод був розроблений Григором Менделем у 1865 році.
Основні принципи гібридологічного аналізу наступні:
1. Організми, що схрещуються повинні належати до одного виду. У дослідах Г.Менделя таким видом був горох посівний. Вважається, що він досить вдало підібрав об’єкт. Горох - рослина самозапильна, з великими квітками, зручними для схрещування, має порівняно виску плодючість і для вирощування не вимагає особливих умов.
2. Організми, що схрещуються повинні чітко розрізнятися по окремих ознаках. Г. Мендель виділив у 22 сортів гороху 7 ознак, кожна із яких мала по два контрастних прояви, наприклад, зріле насіння за формою було гладеньким або зморшкуватим, по кольору сімядолей жовтим або зеленим, зафарбування квітки було білим або пурпуровим, а розташування - пазушним або верхівковим, шкірка насінини мала сірий або білий колір, рослини були високорослими чи карликовими. Слід підкреслити, що у своїх дослідах Г.Мендель використав в якості вихідних форм для схрещування рослини, які відрізнялися порівняно невеликою кількістю контрастуючих ознак.
3. Досліджувані ознаки повинні бути константні, тобто відтворюватися з покоління в покоління при схрещуванні в межах лінії (батьківської форми). Щоб переконатися в константності ознак Мендель два роки попередньо перевіряв різноманітні форми гороху.
4. Необхідна характеристика і кількісний облік всіх класів розщеплення, якщо воно спостерігається в гібридів першого і наступних поколінь. У своїх дослідженнях Г. Мендель вів облік характеру успадкування кожної з досліджуваних ознак, точний кількісний облік гібридних рослин, що відрізнялися окремими ознаками, в ряду послідовних поколінь та індивідуальний аналіз потомства від кожної рослини теж в ряду поколінь.
При гібридологічному аналізі завжди складають генетичні схеми схрещування. Схрещування позначають знаком множення (×). Батьківські форми, що підлягають схрещуванню, позначають літерою Р ( від латинського Parentа— батьки). При написанні схеми скрещування на перше місце звичайно ставлять материнський організм, а на друге — батьківський. Жіночу стать позначають символом ♀ (дзеркало Венери), чоловічу - знаком ♂ (щит і спис Марса). Нащадків від схрещування двох особин із різною спадковістю називають гібридними, а окрему особину - гібридом. Гібридне покоління позначають літерою F (від латинського Filii - діти) із цифровим індексом, що відповідає порядковому номеру гібридного покоління. Наприклад, перше покоління позначають F1, якщо гібридні організми схрещуються між собою, то їхнє потомство позначають F2, третє покоління – F3 і т.д.
Домінуючу ознаку Мендель запропонував позначати великою літерою, а рецесивну - тією ж літерою, але малою.
Схрещування, в якому батьки відрізняються однією парою альтернативних (контрастуючих) ознак, називається моногібридним. Відповідно є дигібридні, тригібридні, полігібридні схрещування.
Гібридологічний аналіз звичайно складається із системи схрещувань, куди входить одержання першого покоління (F1), другого (F2) - від схрещування гібридів F1 між собою і двох, що отримали назву зворотних схрещувань, або беккросів, тобто схрещувань гібрида F1 з однієї та іншою батьківськими формами. Потомство від такого схрещування позначається Fв.
Схрещування двох форм між собою в двох протилежних напрямках називають реципрокними: P1 × Р2 i Р2 × Р1. Наприклад, кролиця чорна × кріль білий і кролиця біла × кріль чорний.
Провівши моногібридне схрещування гороху Г. Мендель помітив, що у рослин першого гібридного покоління з двох альтернативних станів кожної ознаки фенотипово проявляється лише один альтернативний стан. У науці ця закономірність отримала назву першого закону Менделя - закону домінування, або одноманітності гібридів першого покоління. Відповідно до сучасного рівня наших знань цей закон формулюється так: гібриди першого покоління, що походять від гомозиготних батьківських особин, які відрізняються одна від одної альтернативним станом певної ознаки, є повністю одноманітними за генотиповими та фенотиповими структурами відповідної ознаки.
На основі аналізу успадковування ознак у другому поколінні Мендель виявив явище їх розщеплення, тобто встановив, що нащадки другого гібридного покоління розщеплюються на дві фенотипові групи, одна з цих груп представляє відтворену ознаку, характерну для материнської особини, а друга - батьківської. При цьому одна група характеризується фенотиповим проявленням домінантного стану ознаки, а друга – рецесивного. З’ясувалось, що чисельність особин у груп з проявом домінантного стану ознаки завжди втричі більша, ніж у груп з рецесивним проявом цієї ж ознаки. Все це привело Г.Менделя до розуміння того, що розщеплення нащадків у другому гібридному поколінні за фенотиповим проявом різних ознак є не безладним, а упорядкованим. Встановлена закономірність отримала назву закону розщеплення ознак, або другогозакону Менделя, який можна сформулювати так: при схрещуванні двох гетерозиготних особин, тобто гібридів, які аналізуються за однією парою альтернативних ознак, у потомстві спостерігається розщеплення за фенотипом у співвідношенні 3: 1 і за генотипом 1: 2: 1.
При кількісному вивченні розщеплення гібридів зіставляють фактично отримані в досліді дані з теоретично очікуваними відповідно до формули розщеплення (1: 1, 3: 1, 1: 2: 1, 9: 3: 3: 1 і т.п.), тому що повного збігу не буває. Статистична оцінка різниці між фактично отриманими і теоретично очікуваними даними дає можливість з'ясувати, у яких випадках і наскільки ця різниця істотна й у яких випадках вона несуттєва і випадкова.
Розщеплення в гібридних потомствах можна опрацювати статистично тільки в тому випадку, коли поведінка кожної пари алельних генів є незалежною, а поєднання генів при заплідненні випадковим.
Щоб оцінити ступінь відповідності фактично одержаних у досліді даних теоретично очікуваним, у статистиці використовується показник, названий критерієм відповідності χ 2. Слід пам’ятати, що метод χ 2 не можна застосовувати, якщо показники величин досліду виражені у відсотках або в інших відносних величинах і якщо число осіб в одному із теоретично розрахованих класів менше 5. χ 2 вираховують за формулою χ 2=∑ 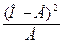 , де ∑ - означає суму, О - одержаний результат; Е - теоретично очікуваний результат (Е). Приклад того як обчислюється χ 2 та послідовність розрахунків, приведені в таблиці 3.
, де ∑ - означає суму, О - одержаний результат; Е - теоретично очікуваний результат (Е). Приклад того як обчислюється χ 2 та послідовність розрахунків, приведені в таблиці 3.
Таблиця 3
Обчислення χ 2 при моногібридному схрещуванні томатів
| Класи розщеплення | Очікуване розщеп-лення | Одержаний результат (О) | Теоретично очікуваний результат (Е) | О-Е | (О-Е)2 | 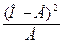
|
| І. Червоні плоди 2. Жовті плоди | +9 -9 | 0, 26 0, 77 | ||||
| Сума | - | χ 2=1, 03 |
Знаючи значення χ 2 при моногібридному схрещуванні, можна оцінити статистичну достовірність розщеплення. З формули випливає, що χ 2 буде тим меншим, чим менша розбіжність між фактично отриманими й очікуваними даними (О—Е), Зазначена розбіжність є в одних випадках результатом дії випадкових причин, у інших - характеризує дійсно існуюче розходження між даними теоретично очікуваними й отриманими в досліді. Щоб зробити правильний висновок про випадковість або закономірність відхилення, отримане значення χ 2 порівнюють із його значенням у таблиці 4.
З табл. 4 випливає, що розмір χ 2 залежить від двох розмірів: числа ступенів свободи (df) і ймовірності (Р). Число ступенів свободи – це число незалежно розрахованих теоретично очікуваних величин. Для з'ясування цього поняття розглянемо найпростіший приклад. Припустимо, що є гібрид гороху, що дав розщеплення за забарвленням насіння на 2 фенотипи (класи): 110 жовтих насінин і 44 зелених. Їх можна уявити як суму, у якої одне зі складових установлюється вільно, а інше залежить від першого. У такому випадку тільки один доданок береться вільно і, отже, ступінь свободи тільки одна. При трьох класах осіб буде 2 ступеня свободи, при чотирьох—3 ступеня свободи і т.д., при п класах df = n -1.
Таблиця 4
Таблиця значень χ 2 при різних ступенях свободи
(по П.Ф. Рокицькому, із скороченням)
| df* | Ймовірність (Р) | |||||||||
| 0, 99 | 0, 95 | 0, 90 | 0, 75 | 0, 50 | 0, 25 | 0, 10 | 0, 05 | 0, 025 | 0, 01 | |
| - | - | 0, 02 | 0, 10 | 0, 45 | 1, 32 | 2, 71 | 3, 84 | 5, 02 | 6, 63 | |
| 0, 02 | 0, 10 | 0, 21 | 0, 58 | 1, 39 | 2, 77 | 4, 61 | 5, 99 | 7, 38 | 9, 21 | |
| 0, 11 | 0, 35 | 0, 58 | 1, 21 | 2, 37 | 4, 11 | 6, 25 | 7, 81 | 9, 35 | 11, 34 | |
| 0, 30 | 0, 71 | 1, 06 | 1, 92 | 3, 36 | 5, 39 | 7, 78 | 9, 49 | 11, 14 | 13, 28 |
df* - число ступенів свободи
Ймовірність (Р), від якої також залежить розмір χ 2 у біологічних дослідженнях, умовно приймають рівною 0, 05. Це означає, що якщо обчислене значення χ 2 не перевищує табличного значення χ 2, що знаходиться в графі з ймовірністю 0, 05, то фактично отримані дані відповідають теоретично очікуваним. Якщо обчислене значення χ 2 буде менше табличного при ймовірності 0, 05 (буде відповідати цифрам, розташованим лівіше цієї графи), то це буде свідчити про більш точну відповідність фактично отриманих даних теоретично очікуваним. Якщо, навпаки, обчислене значення χ 2 буде більше табличного значення при ймовірності 0, 05 (буде відповідати цифрам, розташованим правіше цієї графи), то фактично отримані дані не відповідають теоретично очікуваним (у випадку зчепленого успадковування, селективного запліднення і т.д.).
У розглянутому вище прикладі χ 2при моногібридному схрещуванні томатів дорівнює 1, 03. Так як число класів (фенотипів) у цьому випадку дорівнює двом (червоні і жовті плоди), то число ступенів свободи df дорівнює 1 (2-1). З табл. 4 випливає, що значення χ 2, рівне 1, 03, відповідає ймовірності 0, 25, тобто знаходиться лівіше графи з ймовірністю 0, 05. Це означає, що фактично отримане розщеплення цілком відповідає теоретично очікуваному відношенню 3: 1.
Вище відзначалося, що величина χ 2 залежить від величини відхилення між фактично отриманими і теоретично очікуваними величинами. Але і при однакових відхиленнях показник χ 2 може виявитися різним в залежності від розміру вибірки. Вибіркою, або вибірковою сукупністю, називається частина генеральної сукупності. Генеральна ж сукупність містить у собі всю сукупність осіб, насінин і т.д. Залежність χ 2 від розміру вибірки видна з таблиці 5.
Таблиця 5
Залежність χ 2 від розміру вибірки при моногібридному схрещуванні гороху
| Класи розщеп-лення | Очікуване роз-щеплення | Одержаний результат (О) | Теоретично очікуваний результат (Е) | О-Е | (О-Е)2 | 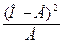
|
| 1. Жовті 2. Зелені | -6 +6 | 0, 31 0, 95 | ||||
| Сума | - | χ 2=1, 26 | ||||
| 1. Жовті 2. Зелені | -6 +6 | 1, 09 3, 27 | ||||
| Сума | - | χ 2=4, 36 |
Отже, при однакових відхиленнях величина χ 2 значно більша при малій вибірці. При числі ступенів свободи, рівному при моногібридному розщепленні 1 (табл. 4), значення χ 2 = 1, 26 менше табличного значення при ймовірності 0, 05. Значення ж χ 2 = 4, 36 більше табличного значення χ 2 при тій же ймовірності 0, 05. Це означає, що в першому випадку при більшому розмірі вибірки фактично отримане розщеплення цілком відповідає теоретично очікуваному відношенню (3: 1). В другому ж випадку при меншому розмірі вибірки фактично отримане розщеплення не відповідає теоретично очікуваному (3: 1). Звідси випливає необхідність аналізувати по можливості великі вибірки.