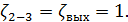В тонкой стенке при постоянном напоре

ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ И НАСАДКОВ

Истечение через малое отверстие

в тонкой стенке при постоянном напоре

При истечении через отверстие в стенке сосуда вся жидкость в нём приходит в движение. Однако средняя скорость v _п в «подходном» живом сечении 1-1 (рис. 6.1) незначительна. Пусть Ω - площадь сечения 1-1, а ω – площадь отверстия. При Ω /ω ≥ 4, скоростью подхода v _п можно пренебречь. При этом ошибка определения полного напора не превысит 5%.

Основная задача при истечении жидкости из отверстий и насадков – определение расхода и скорости истечения.

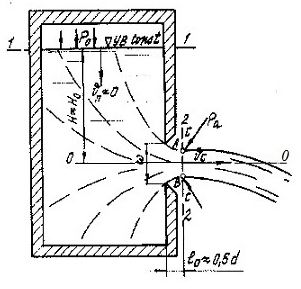Рис. 6.1

- Ω /ω ≥ 4, и скорость подхода пренебрежимо мала;

- скорости U_A и U_B (в верхней и нижней точках сжатого живого сечения) почти равны: U_A ≈ U_B (наблюдается при H≥ 10d, где d - высота отверстия).

Тонкой называют стенку, края отверстия в которой (кромки) заострены так, что вытекающая струя касается стенки по одной линии. В этом случае возможны только местные сопротивления движению жидкости.

Сжатие струи от ω до ω _с обусловлено инерцией частиц жидкости, движущейся при подходе к отверстию по сходящимся криволинейным траекториям.

На пути от выхода из отверстия до сжатого сечения C-C движение резко изменяющееся, а после него - плавно изменяющееся.

Сжатое сечение С-С - первое (после выхода из отверстия), к которому применимо уравнение Бернулли, так как линии тока в сжатом сечении близки к параллельным прямым, и скорости распределяются примерно равномерно.

Введём понятие коэффициента сжатия струи

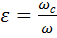. (6.1)

Соединим уравнением Бернулли сечение 1-1 (поверхность жидкости) и сечение 2-2 (сжатое сечение С-С):

.

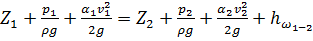Плоскость сравнения проведём через центр тяжести сжатого сечения C-C.

Тогда ; ; ; ; ; ; ;

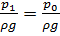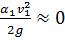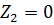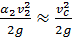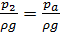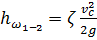где ζ - коэффициент сопротивления, учитывающий потери напора на участке потока между сечениями 1-1 и 2-2. Потери напора сосредоточены в основном у самого отверстия, где скорости уже достаточно велики.

В условиях задачи уравнение Бернулли примет вид:

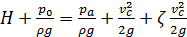. (6.2)

Обозначим

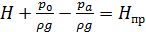, (6.3)

где H _пр называют приведённым напором. Тогда

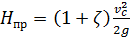, (6.4)

откуда

, (6.5)

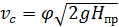, (6.6)

где 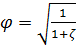- коэффициент скорости, учитывающий потери напора.

При p ₀ =p_a H _пр= H, следовательно,

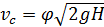. (6.7)

Для идеальной жидкости ζ =0 и φ =1, и справедлива формула Торричелли

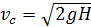. (6.8)

Расход для случая p ₀ =p_a:

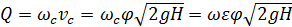
или

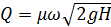. (6.9)

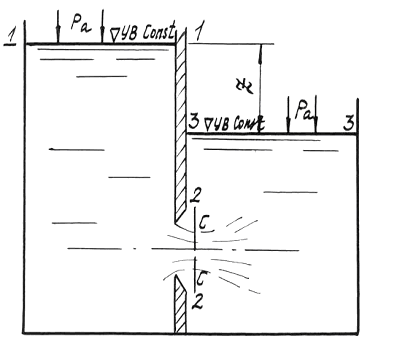Рис. 6.2

отверстия.

Для круглых и квадратных отверстий в

квадратичной области:

ε =0, 63÷ 0, 64; ζ =0, 006; φ =0, 97; μ =0, 62.

При истечении под уровень (затопленное отверстие) в формулу (6.9) вместо H подставляют Z - разность уровней жидкости в сосудах (рис. 6.2):

,

,
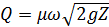