
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Исследования Никурадзе
|
|
Обобщение представлений о потерях напора.
Исследования Никурадзе
Представим себе трубу диаметром D с задвижкой и двумя пьезометрами. При помощи задвижки можно изменять скорость в трубе, для каждой скорости можно по пьезометрам определять потерю напора hl на участке трубы длиной l.
Коэффициент гидравлического трения можно выразить из формулы Вейсбаха-Дарси и определения числа Рейнольдса:
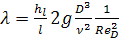 .
.
По этой формуле, определив из опытов hl, vи ν, вычисляют значения λ. Проводя подобные опыты, И. И. Никурадзе исследовал (в 1933 г.) напорные круглоцилиндрические трубы с однозернистой равномерно распределённой искусственной шероховатостью, которую он создавал, наклеивая на стенки трубы песчинки высотой Δ. Результаты опытов Никурадзе представил в виде графика (рис. 5.9). По осям графика отложены величины lgReD и lgλ, но на шкалах осей выписаны сами числа ReD и λ (а не значения их логарифмов).
На график нанесены кривые, вычисленные по приведенной зависимости; каждая кривая отвечает определенной относительной шероховатости 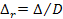 , где Δ - высота выступов шероховатости (Δ мала сравнительно с диаметром D).
, где Δ - высота выступов шероховатости (Δ мала сравнительно с диаметром D).
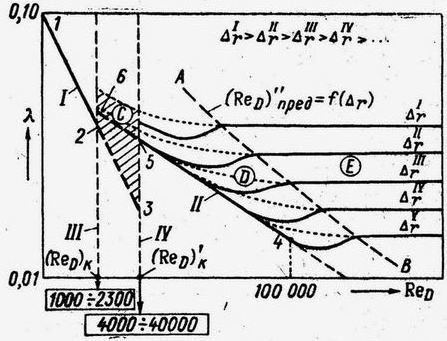 Рис. 5.9
Рис. 5.9
|
1) коэффициент λ, входящий в формулу Вейсбаха-Дарси, в об-щем случае зависит от Δ r и ReD;
2) имеются случаи движения жидкости, когда λ зависит или только от Δ r, или только от ReD;
3) имеются определённые зоны сочетания Δ r и ReD, для которых в зависимости потерь от скорости
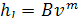 (5.62)
(5.62)
показатель степени m получает определенное значение (1, 2 и т. п.).
На графике показаны две «опорные» линии:
- прямая ламинарного режима I, построенная по уравнению (Лекция 7)
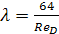 ; (5.63)
; (5.63)
- прямая Блазиуса II, построенная формуле Блазиуса (Лекция 8)
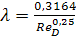 . (5.64)
. (5.64)
Логарифмические координаты позволяют «опорные» линии I и II, выражаемые функциями (5.63) и (5.64), представить в виде прямых. Поле графика разбито на три зоны:
Первая зона - зона ламинарного режима; она представлена прямой 1-2, построенной по уравнению (5.63). Экспериментальные кривые λ = f (ReD), найденные для разных Δ r, сливаются в одну линию, совпадающую с линией 1-2. Для этой зоны:
а) величины ReD относительно малы, ReD < 1000÷ 2300;
б) потеря напора hl не зависит от шероховатости, так как все кривые λ = f (ReD), построенные для разных Δ г, как было отмечено, сливаются в одну прямую 1-2;
в) потери напора hl пропорциональны первой степени скорости v (как то следует из формулы (5.62) при показателе степени m =1);
г) величина λ определяется формулой (5.63).
Вторая зона, расположенная между вертикалями III и IV (заштрихована), -зона неустойчивого режима. Ее называют переходной зоной (внутри её происходит переход ламинарного режима в турбулентный и наоборот). Здесь:
а) числа Рейнольдса лежат в пределах от 1000÷ 2300 до ~4000÷ 40 000;
б) на отдельных участках потока возникают области турбулентного режима, которые разрастаются, а затем исчезают и снова появляются. В связи с этим вторую зону иногда называют зоной перемежающейся турбулентности.
Когда турбулентные области в трубе разрастаются, увеличивается сопротивление движению жидкости (в связи с ростом касательных напряжений трения), при этом скорость уменьшается. Как только она делается меньше критической скорости, разросшиеся турбулентные области обращаются в ламинарные (или выносятся за пределы рассматриваемой части потока); после этого в связи с уменьшением потерь напора (обусловленным переходом турбулентного режима в ламинарный на отдельных участках трубы) скорость увеличивается, причем турбулентные области снова появляются и т. д. В связи с таким характером движения в переходной зоне, представить это движение на графике какими-либо определенными кривыми нет возможности. Исключение могут составить только случаи, когда ламинарный режим «затягивается» и распространяется по длине всего трубопровода (прямая 2-3) или, когда в связи с особыми условиями движения, турбулентный режим имеет место по длине всего трубопровода (линия 5-6).
Третья зона - зона турбулентного режима; она располагается правее вертикали IY, отвечающей ReD =4000÷ 40000. Третья зона, в свою очередь, разбивается на три области.
Первая область - «область гладких русл». Она представлена: а) при числах Рейнольдса ReD < 100000 - прямой линией II и б) при числах Рейнольдса ReD > 100000 - кривой линией, являющейся продолжением прямой II; эта кривая, начинающаяся от точки 4, на рис. 5.9 не показана.
В первой области:
а) потери hl в пределах до чисел ReD =100 000 пропорциональны скорости v в степени 1, 75 (т=1, 75), что следует из формулы Блазиуса (5.64);
б) потери hl не зависят от шероховатости, поскольку все кривые Δ r=const сливаются в одну линию (здесь мы получаем гладкие трубы; выступы шероховатости покрыты ламинарным подслоем);
в) потери hl, а также коэффициент λ, зависят только от числа Рейнольдса, согласно формуле Блазиуса (5.64) или Прандтля
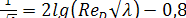 , (5.65)
, (5.65)
то есть
λ = f (ReD). (5.66)
Вторая область - «область доквадратичного сопротивления шероховатых русл», эта область лежит между прямой II и линией АВ.
Кривые Δ r=const в этой области имеют по Никурадзе вид сплошных линий; опыты других авторов дают кривые, показанные штриховыми линиями. Такое расхождение объясняют различием шероховатости, имевшей место при проведении опытов. Считают, что кривые Никурадзе относятся к однозернистой равномерно распределенной шероховатости; штриховые же кривые - к шероховатости разнозернистой, свойственной, например, стальным и чугунным трубам.
Из графика видно, что для второй области λ (и hl) зависят как от числа Рейнольдса, так и от относительной шероховатости:
λ = f (ReD, Δ r). (5.67)
Третья область - «область квадратичного сопротивления шероховатых русл». Эта область располагается правее линии АВ.Здесь:
а) потеря напора прямо пропорциональна квадрату скорости v (т=2, 0);
б) коэффициент λ не зависит от числа Рейнольдса ReD (все линии графика - прямые, параллельные горизонтальной оси);
в) hl и λ зависят только от относительной шероховатости:
λ = f (Δ r). (5.68)