Местные гидравлические сопротивления

При резком изменении формы и размеров поперечного сечения потока
(расширения, сужения, повороты) изменяется поле скоростей, и образуются области, заполненные вихрями. Кинематическая структура течения с образованием отрывов потока от стенок и вихрей показана на рис. 5.10 и 5.11.

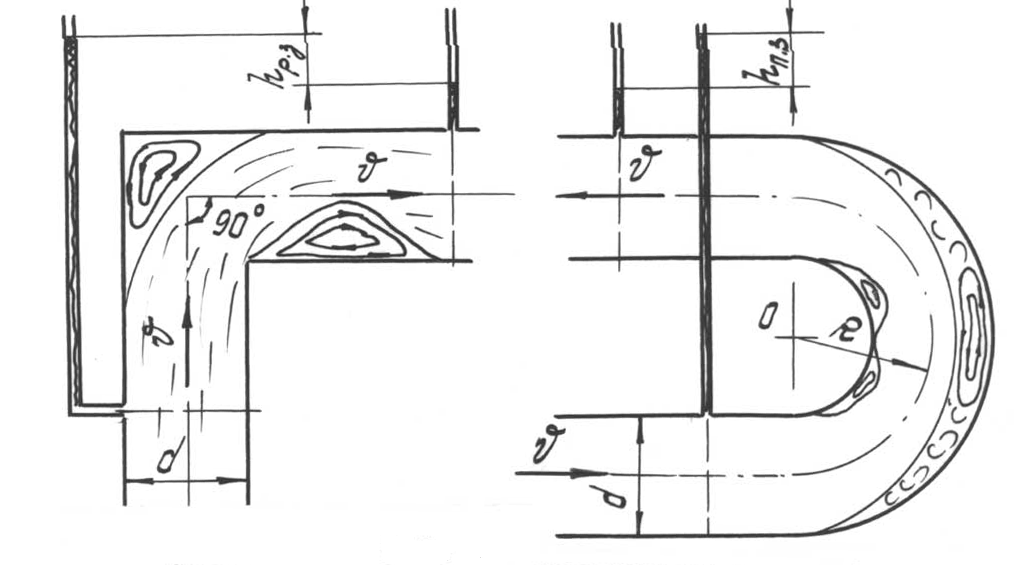
На рис. 5.10 показана схема потока жидкости на повороте: а) при резком повороте (без закругления); б) при плавном повороте.

Крупные вихри интенсифицируют рассеивание энергии, благодаря чему потери в местных сопротивлениях могут намного превосходить потери по длине участка той же протяженности, что и местное сопротивление.

а) б)   Рис. 5.10

Местные потери напора разделяют на группы:

а) потери, связан-ные с изменением живого сечения потока (сред-ней скорости) в случае резкого и плавного расширения в трубопроводах;

б) потери, вызванные изменением направления потока, что встречается в коленах (отводах);

в) потери, связанные с протеканием жидкости через арматуру (вентили, краны, обратные клапаны, сетки и т. п.);

г) потери, связанные с отделением одной части потока от другой, или слиянием двух потоков в один общий, что наблюдается в тройниках, крестовинах и отверстиях в боковых стенках трубопровода при транзитном расходе.

Потери в местных сопротивлениях рассчитывают по формуле Вейсбаха (5.20). Коэффициент ζ _м, входящий в формулу, определяется экспериментально для каждого местного сопротивления.

В некоторых случаях для квадратичной области сопротивлений найдены теоретические зависимости для ζ _м.

При больших числах Re коэффициент ζ _м зависит только от формы граничных поверхностей и не зависит от рода жидкости и скорости течения (т. е. от Re).

При малых числах Re коэффициент ζ _м зависит не только от размеров и геометрической формы граничных поверхностей потока, но также от Re.

Местное сопротивление при внезапном расширении трубы. Выходя из узкой части трубы (рис. 5.11), струя отрывается от стенок, и пространство между струей и стенками заполняется вихрями. На некотором расстоянии l_р струя полностью расширяется, но в сечении 2´ -2´ имеет резко неравномерную эпюру скоростей, что обусловлено искривлением потока на участке l_р. Выравнивание эпюры происходит на переходном участке l_в, в конце которого (сечение 2–2) устанавливается распределение скоростей, характерное для стабилизированного потока. Поскольку перестройка эпюры скоростей сопровождается дополнительными потерями (помимо потерь на трение), то расчетный участок местного сопротивления l ₀ включает водоворотный и переходный участки, то есть l ₀= l_р+l_в.

Выразим потери при внезапном расширении из уравнения Бернулли

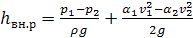. (5.69)

В дальнейшем (для простоты) будем полагать, что α ₁=α ₂=1.

Чтобы исключить разность давлений, применим к отсеку жидкости, ограниченному сечениями 1–1 и 2–2 и боковой поверхностью трубы (контрольная поверхность на рис. 5.11 показана штриховой линией), уравнение количества движения

α ₀ρ Q(v₂-v₁)=(T₀)_s+G_s+P_s+R_s. (5.70)

Здесь α ₀ - корректив количества движения. Для сечений 1–1 и 2–2 можно принять α ₀=1; (T ₀)_S - проекция на направление движения внешней силы трения T ₀, действующей со стороны стенок трубы на рассматриваемый отсек жидкости. Так как длина участка между сечениями 1–1 и 2–2 невелика, то силой T ₀ пренебрегаем. Проекция собственного веса отсека на направление движения G_S =0; P_S - сумма проекций на ось S сил гидродинамического давления P ₁ и P ₂, действующих на торцевые сечения 1–1 и 2–2 отсека; R_S - проекция реакции стенок; R_S=R, где R – сила давления вертикальной стенки (в сечении 1-1), имеющей кольцевую форму.

Сумму P_S+R_S в (5.64) можно представить в виде

P_S+R_S =(P ₁- P ₂)+ R =(P ₁+ R)- P ₂. (5.71)

Измерения показывают, что в сечении 2–2 давление распределяется по гидростатическому закону и P ₂ = p ₂ ω ₂, а в пределах кольцевой площади давление мало отличается от p ₁. Поэтому вместо (5.71) можно написать:

(P ₁+ R)- P ₂=(p ₁ ω ₁+ p ₁ ω _k) - p ₂ ω ₂ = p ₁(ω ₁+ ω _k) - p ₂ ω ₂= p ₁ ω ₂ - p ₂ ω ₂= ω ₂(p ₁ - p ₂).

Теперь, приняв во внимание, что Q = v ₂ ω ₂, вместо уравнения (5.70) получим:

ρ v ₂ ω ₂(v ₂- v ₁)=(p ₁- p ₂) ω ₂.

Следовательно,

.

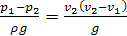Теперь уравнение Бернулли (5.69) можно записать в виде

,

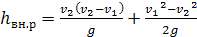который, после упрощений, приводит к формуле Борда:

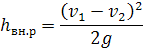
Эта формула показывает, что потеря напора при внезапном расширении потока равна скоростному напору, вычисленному по потерянной скорости (v ₁- v ₂). Используя уравнение неразрывности, формулу Борда можно привести к виду формулы Вейсбаха (5.17), и получить теоретическое выражение для коэффициента сопротивления ζ _M. Действительно, поскольку ω ₁ v ₁= ω ₂ v ₂, то

.

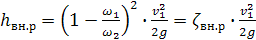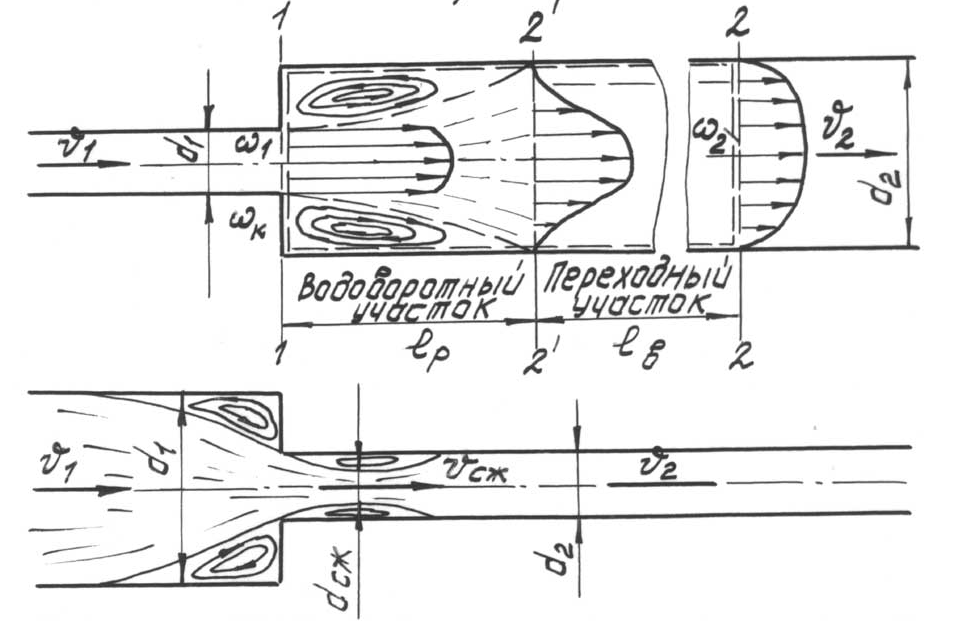Рис. 5.11

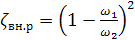. (5.72)

В частном случае, когда 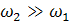, то есть труба сопрягается с большим резервуаром, ζ _вн.р = ζ _вых =1 или h_вых = v ₁²/(2 g). Используя формулу (5.72), следует помнить о допущениях, на которых она построена. Одно из них - предположение о том, что α ₀≈ 1 и α ≈ 1. Поэтому при значительной неравномерности распределения скоростей перед расширением (когда эти коэффициенты существенно отличаются от единицы) формула (5.66) требует уточнения.

Уточнение можно получить, отказавшись от допущения α ₀≈ 1 и α ≈ 1.

Другое допущение связано с влиянием числа Рейнольдса. Влияние проявляется при Re ≤ 5000, а при малых числах Re становится преобладающим, поэтому формула Борда (5.66) дает удовлетворительные результаты лишь в квадратичной области сопротивления.

Заметим, наконец, что формула Борда учитывает только потери на расширение, т.е. то превышение местных потерь над потерями по длине на участке l ₀, которое вызвано увеличением диссипации энергии в местном сопротивлении. Если расчетный участок l ₀= l_р+l_в велик, то потери на трение здесь могут быть сопоставимы с потерями на расширение, и пренебрегать ими нельзя. Поэтому при постановке опыта для определения потерь на расширение следует из потерь, измеренных в опыте, вычесть потери по длине на участке эквивалентной длины. Это замечание относится и к другим видам местных сопротивлений.