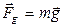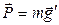Краткая теория. Все тела в природе притягивают друг друга

Все тела в природе притягивают друг друга. Закон, которому подчиняется это притяжение, был установлен Ньютоном и носит название закона Всемирного тяготения. Согласно этому закону сила, с которой две материальные точки притягивают друг друга, пропорциональна массам этих точек и обратно пропорциональна квадрату расстояния между ними:

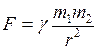, (2.1)

где g – Всемирная гравитационная постоянная, равная ,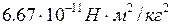

m ₁, m ₂ – массы взаимодействующих точек;

r – расстояние между телами.

Если тела не являются материальными точками, задача нахождения сил взаимодействия усложняется. Но если взаимодействующие тела представляют собой однородные шары или однородный шар и материальную точку, то их взаимодействие описывается формулой (2.1), где под r нужно понимать расстояние между центрами взаимодействующих тел.

Притяжение тел осуществляется через гравитационное поле. Оно проявляет себя в том, что помещенное в него другое тело оказывается под действием силы притяжения. Гравитационное поле имеет две важных характеристики: силовую 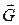и энергетическую j.

Напряженность 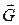гравитационного поля равна:

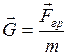, (2.2)

где 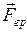– гравитационная сила, действующая на материальную точку массы m.

Потенциалом гравитационного поля j называют:

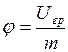, (2.3)

где U_гр – потенциальная энергия, которой обладает в этом поле масса.

Напряженность и потенциал связаны между собой соотношением:

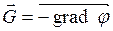. (2.4)

Зная напряженность, можно вычислить разность потенциалов между точками 1 и 2 гравитационного поля:

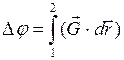. (2.5)

Потенциальную энергию материальной точки массой m в гравитационном поле можно выразить так: 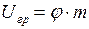, а если гравитационное поле само создано материальной точкой или сферическим телом массой M, то потенциальную энергию материальной точки массой m можно найти следующим образом:

.

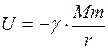Если одно из взаимодействующих тел – Земля, то гравитационная сила называется силой тяжести. Движение под действием этой силы называется свободным падением, а ускорение, вызываемое этой силой, g – ускорением свободного падения.

При точном решении задач о движении тел относительно земной поверхности нужно учитывать центробежную силу инерции, возникающую во вращающейся (по отношению к инерциальным системам) системе отсчета. Она равна (рис. 2.1):

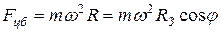(2.6)

где m – масса тела,

w – угловая скорость суточного вращения Земли,

R_З – радиус Земли,

j – широта местности.

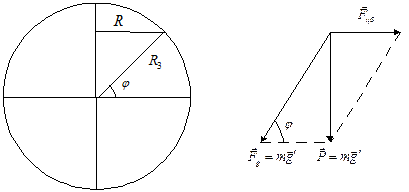
Рис. 2.1

Наблюдаемое относительно Земли ускорение свободного падения тел 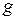обусловлено действием силы 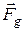, с которой тело притягивается Землей, и силы 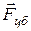. Результирующая этих сил 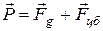есть сила тяжести, равная 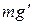( – ускорение свободное падения, учитывающее вращение Земли).

Отличие силы тяжести 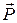от силы притяжения к Земле 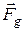невелико, так как центробежная сила инерции значительно меньше, чем 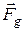. Разность 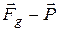равна нулю на полюсах и достигает максимума, равного 0, 3% силы 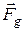, на экваторе. Из-за сплюснутости Земли у полюсов сила 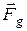сама по себе несколько варьирует с широтой, будучи на экваторе примерно на 0, 2% меньше, чем у полюсов. В итоге ускорение свободного падения изменяется с широтой в пределах от 9, 780 м/с ² на экваторе до 9, 832 м/с ² на полюсах. Значение g =9, 80665 м/с ² принято в качестве нормального (стандартного) значения.

Методика проведения измерений и описание установки

Эксперимент состоит в определении ускорения свободного падения тел различной массы.

Общий вид установки Атвуда показан на рисунке 2.2.

На вертикальной колонне 1, установленной на основании 2, закреплены три кронштейна: неподвижный нижний кронштейн 3 и два подвижных: средний 4 и верхний 5, а также верхняя втулка 6. На верхней втулке закреплен ролик 7 и электромагнит 11. Через ролик проходит нить 12 с привязанными на ее концах грузиками 14 и 8.

Электромагнит, после подведения к нему питающего напряжения, при помощи фрикционной муфты, удерживает систему ролика с грузиками в состоянии покоя.

Верхний и средний кронштейны можно перемещать вдоль колонки и фиксировать в любом положении, устанавливая таким образом длину пути равномерноускоренного и равномерного движений грузика 14. Для облегчения определения этих путей на колонке имеется миллиметровая шкала, все кронштейны имеют указатель положения, а верхний кронштейн - дополнительную черту, облегчающую точное согласование нижней грани верхнего, большого грузика с определенным началом пути движения.

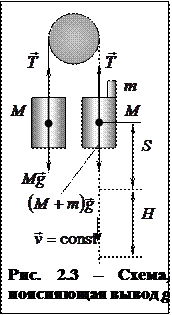На среднем кронштейне закреплен кронштейн 9 и фотоэлектрический датчик 10. Кронштейн 9 снимает с падающего вниз большого грузика дополнительный грузик 13, а фотоэлектрический датчик в это время образует электрический импульс, сигнализирующий начало равномерного движения больших грузиков. Оптическая ось фотоэлектрического датчика (черта на его корпусе) находится на уровне указателя положения среднего кронштейна.

Нижний кронштейн оснащен фотоэлектрическим датчиком с оптической осью на уровне указателя положения кронштейна, после пересечения которой нижней гранью падающего грузика образуется электрический сигнал, указывающий прохождение грузиками определенного пути.

На основании прибора, прикрепленного к нему жестко, находится миллисекундомер РМ-15.

Через ролик, смонтированный на подшипнике таким образом, чтобы он мог вращаться с возможно малым сопротивлением, проходит нитка с двумя одинаковыми грузиками массой М каждый (14 и 8). Система при этом находится в равновесии.

Если по одну сторону блока прибавим небольшой грузик массой m (13), тогда система получит ускорение под влиянием силы mg и, передвигаясь с ускорение а, пройдет путь S.

По второму закону Ньютона для грузиков слева и справа (рис. 2.3):

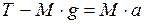, (2.7)

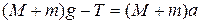. (2.8)

Решая систему этих уравнений, получим:

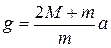(2.9)

Из законов кинематики

, (2.10)

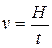, (2.11)

где t – время, в течение которого грузик 14 пройдет путь Н, двигаясь равномерно.

Из формул (2.9) и (2.10) ускорение a равно:

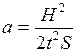. (2.12)

Подставляя (2.11) в (2.8), получим расчетную формулу для нахождения ускорения свободного падения:

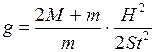. (2.13)

Формула (2.13) выведена в предположении, что сила трения и масса ролика нити пренебрежимо малы, нить нерастяжима.