
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткая теория. Плоским называется такое движение, при котором все точки тела двигаются параллельно одно плоскости
|
|
Плоским называется такое движение, при котором все точки тела двигаются параллельно одно плоскости. Плоское движение твердого тела можно представить как совокупность поступательного движения, происходящего со скоростью центра масс 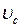 и вращательного вокруг оси, проходящей через этот центр, с угловой скоростью w.
и вращательного вокруг оси, проходящей через этот центр, с угловой скоростью w.
 Рассмотрим в качестве примера скатывание тел с наклонной плоскости (рис. 5.1). Будем предполагать, что при движении не возникает скольжения. Это означает, что скорость тела в точке касания А равна нулю. Отсутствие скольжения обеспечивается действием сил со стороны наклонной плоскости на тело. Эти силы сводятся к силе реакции опоры
Рассмотрим в качестве примера скатывание тел с наклонной плоскости (рис. 5.1). Будем предполагать, что при движении не возникает скольжения. Это означает, что скорость тела в точке касания А равна нулю. Отсутствие скольжения обеспечивается действием сил со стороны наклонной плоскости на тело. Эти силы сводятся к силе реакции опоры 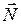 и к касательной силе трения
и к касательной силе трения 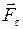 . При отсутствии скольжения сила
. При отсутствии скольжения сила 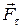 есть сила трения покоя.
есть сила трения покоя.
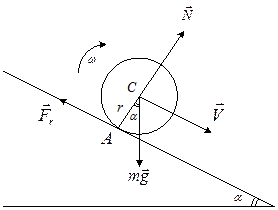
Рис. 5.1 – Плоское движение тела, скатывающегося с наклонной плоскости
Запишем уравнение динамики вращательного движения относительно оси, проходящей через центр масс С:
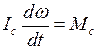 ,
,
где Ic – момент инерции тела относительно оси, проходящей через центр масс С,
Мс – момент внешних сил относительно оси С.
Момент внешних сил создает только сила трения, так как другие силы (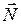 и
и 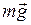 ) проходят через центр тяжести тела.
) проходят через центр тяжести тела.
Момент силы трения 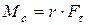 (r – радиус тела), а поэтому
(r – радиус тела), а поэтому
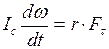 . (5.2)
. (5.2)
Еще одно уравнение дает Второй закон Ньютона:
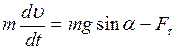 . (5.3)
. (5.3)
Учитывая, что 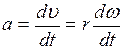 и разрешив полученные уравнения относительно а, получим:
и разрешив полученные уравнения относительно а, получим:
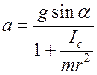 . (5.4)
. (5.4)
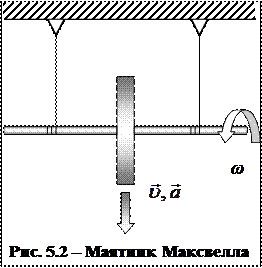 В случае маятника (диска) Максвелла (рис. 5.2), представляющего собой тело, обладающее симметрией вращения, висящего в горизонтальном положении на двух намотанных на него нерастяжимых невесомых нитях, а затем опускающегося под действием силы тяжести, угол
В случае маятника (диска) Максвелла (рис. 5.2), представляющего собой тело, обладающее симметрией вращения, висящего в горизонтальном положении на двух намотанных на него нерастяжимых невесомых нитях, а затем опускающегося под действием силы тяжести, угол 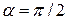 . Тогда из уравнения (5.4) получим:
. Тогда из уравнения (5.4) получим:
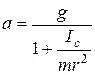 (5.5)
(5.5)
Учитывая, что движение спускающегося на нитях тела равноускоренное, при чем начальная скорость равна нулю, используем формулу 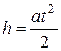 . из уравнения (5.5) получим
. из уравнения (5.5) получим
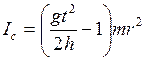 . (5.6)
. (5.6)
Эту же формулу можно получить более простым путем из закона сохранения энергии в его механической форме. Этим законом здесь можно пользоваться даже при наличии силы трения. При отсутствии скольжения, т.е. если считать нить нерастяжимой, сила трения приложена к тем точкам тела, которые лежат на мгновенной оси вращения. Мгновенная скорость таких точек равна нулю, а поэтому приложенная к ним сила трения покоя работы не производит.
В верхней точке тело обладает потенциальной энергией в поле тяжести земли 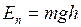 . Эта энергия в нижней точке переходит в кинетическую энергию, которая складывается из энергии поступательного и вращательного движения. Таким образом, получим:
. Эта энергия в нижней точке переходит в кинетическую энергию, которая складывается из энергии поступательного и вращательного движения. Таким образом, получим:
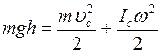 . (5.7)
. (5.7)
Учитывая, что 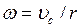 , а также то, что при равноускоренном движении
, а также то, что при равноускоренном движении 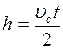 , из формулы (5.7) получим уравнение (5.6).
, из формулы (5.7) получим уравнение (5.6).
В работе используется маятник со сменными кольцами. Из определения момента инерции
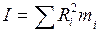 (5.8)
(5.8)
следует, что эта величина аддитивна. Это означает, что момент инерции тел относительно некоторой оси равен сумме моментов инерции частей тела относительно той же оси.
Момент инерции однородного цилиндра относительно его геометрической оси определяется по формуле:
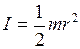 , (5.9)
, (5.9)
где m – масса цилиндра,
r – его радиус.
Момент инерции полого цилиндра (кольца) определяется по формуле:
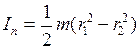 , (5.10)
, (5.10)
где m – масса полого цилиндра (кольца),
r 1 – внешний радиус,
r 2 – внутренний радиус.