
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткая теория. Вращательным движением тела относительно неподвижной оси называется такое движение, при котором все точки тела движутся по окружностям
|
|
Вращательным движением тела относительно неподвижной оси называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Ограничимся рассмотрением движения абсолютно твердых тел, т.е. будем считать, что деформациями тел в рассматриваемой нами задаче можно пренебречь.
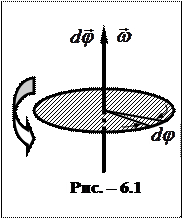 Пусть за время
Пусть за время  радиус-вектор произволь-ной точки тела, например диска, покзанного на рисунке 6.1, совершает поворот на угол
радиус-вектор произволь-ной точки тела, например диска, покзанного на рисунке 6.1, совершает поворот на угол  . Приписав
. Приписав  направление вдоль оси вращения, связанное с направлением вращения правилом правого винта, можем рассматривать бесконечно малый поворот как вектор
направление вдоль оси вращения, связанное с направлением вращения правилом правого винта, можем рассматривать бесконечно малый поворот как вектор 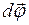 .
.
Быстрота вращения характеризуется угловой скоростью вращения, которая определяется соотношением:
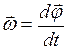 , (6.1)
, (6.1)
а быстрота изменения 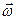 – угловым ускорением:
– угловым ускорением:
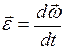 . (6.2)
. (6.2)
Каждая точка вращающегося тела, находящаяся на расстоянии r от оси вращения, движется с линейной скоростью 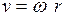 и нормальным ускорением
и нормальным ускорением  . Быстрота изменения модуля линейной скорости v характеризуется тангенциальным ускорением
. Быстрота изменения модуля линейной скорости v характеризуется тангенциальным ускорением 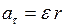 .
.
Мерой инертности тела при вращательном движении является его момент инерции 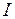 . По определению, каждый элемент объема тела
. По определению, каждый элемент объема тела 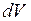 , имеющий массу
, имеющий массу 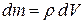 (
( - плотность тела) и находящийся на расстоянии r от оси вращения, обладает моментом инерции
- плотность тела) и находящийся на расстоянии r от оси вращения, обладает моментом инерции
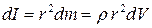 . (6.3)
. (6.3)
Соответственно момент инерции тела объёмом V определяется формулой:
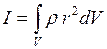 (6.4)
(6.4)
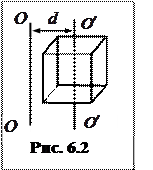 Вычисление момента инерции по формуле (6.4) для неоднородного тела сложной формы может оказаться весьма сложной математической задачей. Ее решение нередко облегчается при использовании теоремы Штейнера, согласно которой момент инерции I тела относительно произвольной оси ОО (например, куб на рисунке 6.2) равен сумме его момента инерции I 0 относительно оси
Вычисление момента инерции по формуле (6.4) для неоднородного тела сложной формы может оказаться весьма сложной математической задачей. Ее решение нередко облегчается при использовании теоремы Штейнера, согласно которой момент инерции I тела относительно произвольной оси ОО (например, куб на рисунке 6.2) равен сумме его момента инерции I 0 относительно оси 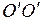 , параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
 . (6.5)
. (6.5)
Экспериментальная проверка этого соотношения является одной из целей данной работы.
Действие некоторой силы 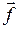 на тело при вращении вокруг неподвижной оси
на тело при вращении вокруг неподвижной оси 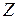 (рис. 6.3) определяется ее моментом относительно данной оси
(рис. 6.3) определяется ее моментом относительно данной оси 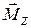 , который по определению равен:
, который по определению равен:
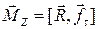 (6.7)
(6.7)

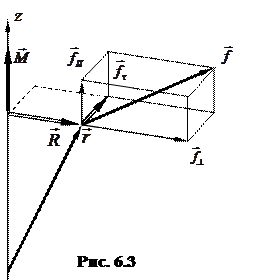 где
где  – перпендикулярная оси Z составляющая радиус-вектора
– перпендикулярная оси Z составляющая радиус-вектора  , проведенного из любой принадлежащей оси Z точки в точку приложения силы;
, проведенного из любой принадлежащей оси Z точки в точку приложения силы;
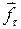 – составляющая силы
– составляющая силы 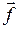 , перпендикулярная плоскости, образованной осью Z и
, перпендикулярная плоскости, образованной осью Z и 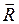 .
.
Составляющие силы 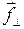 , перпендикулярная оси Z, и
, перпендикулярная оси Z, и 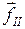 , параллельная ей, момента силы относительно оси Z не создают.
, параллельная ей, момента силы относительно оси Z не создают.
При рассмотрении вращательного движения тела аналогом его импульса при поступательном движении является момент импульса 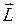 . По определению момент импульса материальной точки, расположенной в точке с радиус-вектором
. По определению момент импульса материальной точки, расположенной в точке с радиус-вектором 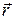 на расстоянии
на расстоянии 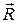 от оси вращения и обладающей импульсом
от оси вращения и обладающей импульсом 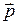 (аналогично тому, как это показано на рис. 6.3),
(аналогично тому, как это показано на рис. 6.3),
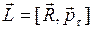 , (6.8)
, (6.8)
где 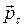 – составляющая импульса
– составляющая импульса 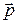 , перпендикулярная плоскости, образованной осью Z и
, перпендикулярная плоскости, образованной осью Z и 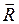 .
.
Твердое тело можно рассматривать как систему N жестко связанных материальных точек с моментами импульса 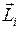 у каждой. Момент импульса тела в этом случае определяется как
у каждой. Момент импульса тела в этом случае определяется как  , и можно доказать, что
, и можно доказать, что
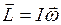 , (6.9)
, (6.9)
где 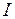 – момент инерции тела;
– момент инерции тела;
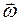 – вектор угловой скорости тела.
– вектор угловой скорости тела.
Основное уравнение динамики вращательного движения (уравнение движения или аналог второго закона Ньютона для вращательного движения) имеет вид:
 . (6.10)
. (6.10)
В частном случае для абсолютно твердого тела, у которого I = const
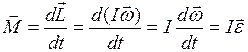 . (6.11)
. (6.11)
Уравнение (6.11) является следствием основных положений классической механики применительно к вращательному движению абсолютно твердого тела, и его экспериментальная проверка является второй целью настоящей работы.