
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эластичность функции
|
|
Рассмотрим функцию у = f(x), где х ≥ 0 и у ≥ 0. Пусть ∆ х – изменение аргумента х. Соответствующее ему изменение функции ∆ y = f(x + ∆ х) – f(x). Рассмотрим относительные изменения величин х и у:

Таким образом, эластичность функции у = f(x) равна производной этой функции, умноженной на отношение аргумента к значению функции.
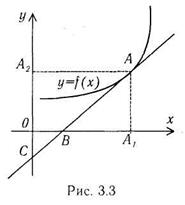
Геометрический смысл эластичности проиллюстрирован на рис. 3.3. Пусть прямая ВС – касательная к графику функции у = f(x) в точке А. Точка В – пересечение касательной с осью х, точка С – пересечение касательной с осью у. Тогда эластичность функции у = f(x) в точке А есть отношение длин отрезков АС и АВ:
 (3.3)
(3.3)
↑ Действительно, пусть А1 и А2 – абсцисса и ордината точки А. Эластичность функции у = f(x) в точке А по определению:
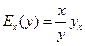 .
.
Из рис. 3.3 видно, что х=│ 0А1│, у=│ 0А2│, а 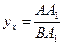 по свойству производной, поэтому
по свойству производной, поэтому 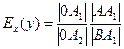 .
.
Из подобия треугольников АА1В и АА2С следует соотношение 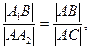 кроме того,
кроме того, 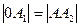 и
и 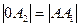 .
.
Следовательно, 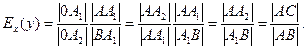
Случай иного расположения точек пересечения касательной возрастающей функции с координатными осями рассматривается аналогично. Если функция убывает, то точка А расположена между точками В и С, рассуждая аналогично,
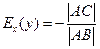 (3.3′) ↑
(3.3′) ↑
Найдём, для каких функций функция эластичности постоянна. По определению (3.2)
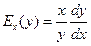 .
.
Пусть Ех(у) = const, т.е. всегда равна некоторому числу Е:
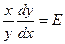 , тогда
, тогда 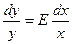 или lny=Elnx+lna,
или lny=Elnx+lna,
где а – константа интегрирования. Тогда у = а хE.
Таким образом, эластичность степенной функции равна показателю степени и не зависит от аргумента. По этой и другим причинам степенную функцию удобно использовать в экономических моделях в качестве простейшей аналитической функции, описывающей зависимость различных параметров.
Пусть D = D(P) – функция спроса. Рассмотрим эластичность спроса:
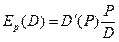 .
.
Функция эластичности спроса в зависимости от цены – удобный экономический показатель, характеризующий изменение спроса. В отличие от производной функции спроса в зависимости от цены, эластичность – безразмерна и не зависит от выбранного масштаба.
В большинстве случаев спрос убывает с ростом цены, в этих случаях эластичность отрицательна. В моделях знак эластичности, как правило, не имеет значения и для удобства рассматривается модуль функции эластичности.
Пусть 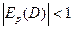 или
или 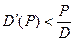 .Т.е. скорость изменения спроса в зависимости от цены меньше темпа изменения цены, отнесённой к спросу. Если цена возрастает, то скорость уменьшения спроса меньше скорости роста цены. Если цена убывает, то скорость роста спроса меньше скорости уменьшения цены. Такой спрос называется неэластичным.
.Т.е. скорость изменения спроса в зависимости от цены меньше темпа изменения цены, отнесённой к спросу. Если цена возрастает, то скорость уменьшения спроса меньше скорости роста цены. Если цена убывает, то скорость роста спроса меньше скорости уменьшения цены. Такой спрос называется неэластичным.
Пусть  или
или 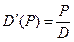 . Т.е. скорость изменения спроса равна скорости изменения цены. Спрос имеет единичную эластичность.
. Т.е. скорость изменения спроса равна скорости изменения цены. Спрос имеет единичную эластичность.
Пусть 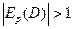 или
или 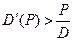 . Т.е. скорость изменения спроса в зависимости от цены больше темпа изменения цены, отнесённой к спросу. Такой спрос называется эластичным.
. Т.е. скорость изменения спроса в зависимости от цены больше темпа изменения цены, отнесённой к спросу. Такой спрос называется эластичным.
Эластичность функции используется для анализа и других экономических понятий, например, предложения.
На практике, если нет аналитического описания функции, формулу (3.2) невозможно использовать для расчёта эластичности. Часто предполагают зависимость степенной: D(P) = а РЕ. Для определения параметров – этой функции достаточно знать значение спроса для двух значений цены: D1 = D(P1) и D2 = D(Р2), для степенной функции: 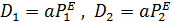 .
.
Тогда 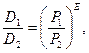 откуда
откуда 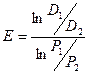 .
.
Этот метод даёт хорошее приближение для практических расчётов.