Модель межотраслевого баланса Леонтьева

Задача межотраслевого баланса сводится к решению системы балансовых уравнений (1) n -го порядка по определению неизвестных X_i (i = 1,..., n). Казалось бы, задача должна иметь единственное решение. В действительности, помимо одноиндексных неизвестных объемов продукции по каждой отрасли X_i неизвестны и все двухиндексные переменные X_ij, характеризующие потоки продукции из одной отрасли в другую. Поэтому число неизвестных (п+п²) больше числа уравнений и задача имеет бесконечное множество решений.

Выход из этого положения был предложен в 1930г. американским экономистом В.В. Леонтьевым на основании изучения структуры экономики США. Балансовая модель Леонтьева базируется на следующих допущениях:

а) рассматриваемые отрасли, на которые разбит производственный сектор страны, считаются чистыми. Термин «чистая отрасль» означает, что продукция каждой из отраслей предполагается однородной, т.е. отрасль выпускает продукт только одного типа и разные отрасли выпускают разные продукты;

б) рассматривается статическая, неизменная за некоторый промежуток времени сложившаяся технология производства. Этот промежуток времени может быть равен одному календарному периоду (скажем, году);

в) имеет место прямо пропорциональная, т.е. линейная зависимость между потоками продукции из одной отрасли в другую X_ij и объемами продукции X_i, выпускаемыми отраслями:

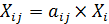(5.2)

где а_ij – коэффициенты пропорциональности, называемые коэффициентами прямых затрат (а_ij ≥ 0).

Зависимость (5.2) следует из предложения В.В. Леонтьева считать структуру затрат в каждой отрасли неизменной. Иными словами, характеризующие структуру затрат отношения а_ij, постоянны:

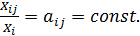(5.3)

Коэффициенты прямых затрат как безразмерные величины имеют двоякий экономический смысл. Если балансовая модель разрабатывается в натуральных из­мерителях, то величина а_ij характеризует количество единиц продукции i -й отрасли (или i -гo продукта), необходимое для изготовления единицы j -го продукта. При записи межотраслевого баланса в стоимостном выражении величина а_ij – доля стоимости продукции i -той отрасли в стоимости единицы продукции j -той отрасли. Например, если бы первой отраслью была угольная промышленность (i = 1), а второй – производство электроэнергии (j = 2), то а₁₂ выражает долю затрат каменного угля, израсходованного на производство электроэнергии, к общей выработке электроэнер­гии; а₂₁ – долю затрат электроэнергии на производство каменного угля в общей выработке каменного угля.

Допущение (5.3) не вполне строго. Однако отличие коэффициентов прямых затрат в крупномасштабных моделях настолько мало, что без ущерба для точности модели их можно считать постоянными. Это допущение делает систему (5.1) легко решаемой, так как от двух групп неизвестных X_ij и X_i переходим к одной группе неизвестных – X_i. Действительно, подставляя (5.2) в уравнения (5.1), получим систему:

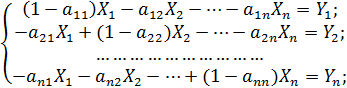(5.4)

или короче

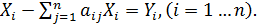(5.5)

Решение этой системы п- гопорядка относительно п неизвестных X_i затруднений не вызывает.

Система уравнений (5.4) или (5.5) называется системой уравнений межотраслевого баланса, или экономико-математической моделью межотраслевого баланса производства и распределения продукции (моделью Леонтьева).

Систему уравнений (5.4) или (5.5) удобно представить в компактной матричной форме. Это дает возможность легко получить ее решение в общем виде.

Введем следующие обозначения:

а) X – матрица-столбец переменных (Х₁, Х₂,..., Х_п) порядка (n x 1)

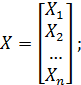
б) А – матрица коэффициентов прямых затратпорядка (п х п)

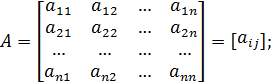
в) Е – единичная матрица порядка (п х п)

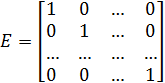
г) Y – матрица-столбец свободных членов (Y₁, Y₂,..., Y_n) порядка (n x 1)

Тогда систему уравнений (4) легко записать в матричной форме:

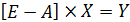(5.6)

Отсюда, решение системы уравнений межотраслевого баланса (5.6) в матричной форме имеет вид:

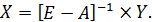(5.7)

Система уравнений (5.6) с ее решением (5.7) и интерпретацией матриц [Е – А] и Y называется моделью Леонтьева в линейной и статической постановке.