Назначение и использование сетевой модели и ее элементы

Создание сложной техники и крупных объектов (например, компьютеров, самолетов, судов, автомобилей, строительных сооружений и т.п.) требует объединения усилий нескольких коллективов людей: проектных и научно-исследовательских учреждений, предприятий и т.д. Чтобы завершить создание сложной техники или объектов к определенному сроку, необходимо увязать выполнение работ всеми исполнителями по времени, стоимости, ресурсам, другим технико-экономическим показателям. Такая увязка осуществляется с помощью планирования и управления выполнения работ всеми исполнителями. Планирование значительно облегчается, если создать некоторую модель, в которой были бы отражены процессы, протекающие при изготовлении или проектировании изделий. Такая модель наиболее эффективно и адекватно описывается методами сетевого планирования и управления (СПУ). Система методов СПУ предназначена для планирования сложных процессов путем при­менения сетевых графиков.

Система СПУ представляет собой комплекс графических и расчетных методов с целью моделирования, анализа и оптимизации плана работ по проектированию или изготовлению некоторого изделия. Основным плановым документом в системе СПУ является сетевой график (сетевая модель или просто сеть), представляющий собой безмасштабное графическое изображение планируемого процесса и отражающий взаимосвязь и последовательность входящих в него работ.

Объектом управления в системах СПУ является коллектив исполнителей, располагающий определенными материальными и финансовыми ресурсами и выполняющий комплекс работ, направленных на достижение конечного результата в установленные сроки.

Система СПУ охватывает следующие этапы планирования и управления комплексом работ:

1. Выявление работ, которые необходимо произвести в процессе проектирования или изготовления некоторого изделия.

2. Построение сетевого графика на основе предварительно составленного перечня работ и связей между ними.

3. Установление количественных оценок по каждой работе (время, стоимость, ресурсы).

4. Расчет параметров сетевого графика.

5. Анализ и оптимизация сетевого графика с целью получения оптимальных показателей (минимальное время работ, минимальная стоимость, максимальная экономия ресурсов).

6. Использование сетевого графика для управления ходом работ.

Наиболее разработанной в настоящее время является СПУ, в которой в качестве входной информации используется только время (временные параметры) и отсутствуют данные о стоимости работ и затраченных ресурсах. С помощью такой системы производится расчет и оптимизация по времени процесса выполнения комплекса работ.

Таким образом, для того, чтобы составить план работ по осуществлению больших и сложных проектов, состоящих из многих сотен и тысяч отдельных опера­ций, необходимо описать его с помощью некоторой математической модели. Таким средством описания проектов (программ) является сетевая модель.

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданных в специфической форме сети, гра­фическое изображение которой называется сетевым графиком.

В основе понятия сетевого графика лежит теория графов. Здесь под графом подразумевается схема, состоящая из заданных точек – вершин. Эти точки соединя­ются между собой определенной системой линий, которые называются ребрами, или дугами графа. Ребра могут быть ориентированными (тогда они называются дугами и снабжаются стрелками, рис 6.1, а) и неориентированными. Если граф имеет кратные ребра, то он называется мультиграфом (рис 6.1, б).

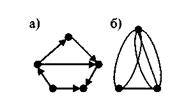
Рис. 6.1. Виды графов

Граф без кратных ребер именуется обыкновенным. Графы могут быть конечными и бесконечными. Если число ребер у графа конечно, то он называется конеч­ным; при бесконечно большом числе ребер граф бесконечный. Граф плоский, если он может быть изображен на плоскости так, что его дуги не пересекаются.

В сетевых графиках используются, в основном, обыкновенные, ориентированные, плоские графы.

Основоположником теории графов является Л. Эйлер, предложивший ее основные идеи в середине XVIII в. Как самостоятельная математическая дисциплина теория графов сформировалась лишь в 30-е годы XX в. при значительном вкладе в ее становление и развитие советских, американских, немецких, французских и других математиков.

Одной из основных конструкций графа, представляющего собой сеть в экономических приложениях, является путь. Путь – это последовательность дуг, позволяющих пройти из одной вершины в другую, причем каждая дуга встречается в пути не более одного раза. Замкнутый путь, соединяющий вершину с ней же самой, называется контуром (циклом).

Руководствуясь терминологией теории графов, сетевой график – это конечный, плоский, ориентированный граф без контуров, дуги которого имеют одну или несколько числовых характеристик.

Главными элементами сетевого графика являются работы и события. Работами называются любые протяженные во времени действия, которые приводят к достижению определенных результатов; работы соответствуют дугам графа. События – это моменты завершения работы; они соответствуют вершинам графа. Продолжительность работы измеряется в единицах времени (часы, дни, недели, декады и др.); работы могут иметь и другие количественные показатели – трудоёмкость, стоимость и т.п.

В сетевом графике могут быть несколько разновидностей работ: действительная работа, ожидание, фиктивная работа. Действительной называется работа, требу­ющая затрат времени и ресурсов: например, изготовление узла машины, составление программы для ПК и др. Ожиданием называется работа, которая требует затрат времени, но не требует затрат ресурсов: например, процесс затвердения бетона; созревание урожая и т.п. Фиктивная работа отражает логическую связь между работами и не требует затрат времени и ресурсов. Она указывает, что возможность начала одной работы непосредственно зависит от результатов другой: например, передача чертежей из конструкторского бюро в цех для изготовления деталей; передача программы для ПК оператору с целью ввода ее в оперативную память и последующей отладки и др.

Действительные работы и ожидания изображаются на графике сплошными линиями, фиктивная работа – пунктирными. Количественные показатели работ проставляются над стрелками (рис. 6.2).

События соответствуют результатам произведенной работы: штамп изготовлен, узел спроектирован, программа для ПК отлажена.

Событие представляет собой только момент совершения работы (работ) и может быть отправным моментом для начала последующих работ. События изображают кружками, внутри кружка – номер события (см. рис 6.2).

Различают предшествующие данной работе события i (например, для работы «составление программы» предшествующим событием может являться «схема алгоритма расчета составлена») и последующие за данной работой события j (например, для работы «составление программы» последующим событием является «программа составлена»). На рис. 6.2 примером предшествующего события может быть событие 3, а последующим – событие 5. Работа между событиями i и j обозначается как (i, j).

Первоначальное событие в сети, отражающее начало определенного комплекса и не имеющее входящих в него работ, называется исходным I (событие 1 на рис. 6.2). Событие, отражающее конечную цель определенного комплекса работ и не имеющее выходящих из него работ, называется завершающим С (событие 7 на рис. 6.2).

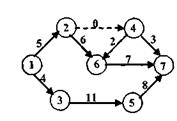
Рис. 6.2. Элементы сетевого графика

Последовательность работ, приводящая от одного события к другому и в которой каждая работа встречается не более одного раза, составляет путь. Может быть несколько полных путей от исходного события I до завершения события С. Полный путь, имеющий наибольшую продолжительность, называется критическим. Кроме того, используются понятия пути, предшествующего данному событию i – от исходного (1) до данного события (i), а также пути, последующего за данным событием i – от данного (I) до завершения события (С).