
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. 1) Определение напряжения смещения нейтрали.
|
|
1) Определение напряжения смещения нейтрали.
Напряжение смещения нейтрали U0 может быть найдено методом узловых потенциалов
 0 = (
0 = ( А Y A +
А Y A +  В Y В +
В Y В +  С Y С)/(Y А + Y В + Y С + Y 0), (4.4.1)
С Y С)/(Y А + Y В + Y С + Y 0), (4.4.1)
где  А,
А,  В,
В,  С – фазные напряжения фаз А, В и С;
С – фазные напряжения фаз А, В и С;
Y А, Y В, Y С и Y 0 – проводимости фаз А, В, С и нулевого провода.
Все величины должны быть записаны в комплексном виде в алгебраической и показательной формах.
При соединении фаз звездой действующие значения фазных Uф. и линейных Uл. напряжений связаны соотношением
Uф. = Uл./ 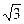 (4.4.2)
(4.4.2)
Таким образом,
UА = UВ = UС = 660/ 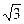 = 380 В.
= 380 В.
Комплексы напряжений, сопротивлений и проводимостей в показательной и алгебраической формах:
 А = 380 е
А = 380 е 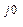 = (380 + j0) В;
= (380 + j0) В;
 В = 380 е
В = 380 е 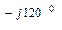 = (-190 – j328) В;
= (-190 – j328) В;
 С = 380 е
С = 380 е 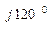 = (-190 + j328) В;
= (-190 + j328) В;
Z А = 8 + j6 = 10 е 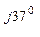 Ом;
Ом;
Y А = 1/ Z А = 1/ 10 е 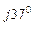 = 0, 1 е
= 0, 1 е 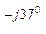 = (0, 08 – j0, 06) См;
= (0, 08 – j0, 06) См;
Z В = 6 – j8 = 10 е 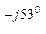 Ом;
Ом;
Y В = 1/ Z В = 1/10 е 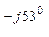 = 0, 1 е
= 0, 1 е 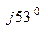 = (0, 06 + j0, 08) См;
= (0, 06 + j0, 08) См;
Z С = 23 + j15, 3 = 27, 6 е 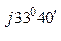 Ом;
Ом;
Y С = 1/ Z С = 1/27, 6 е 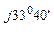 = 0, 0362 е
= 0, 0362 е 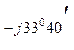 = (0, 03 – j0, 02) См;
= (0, 03 – j0, 02) См;
Z 0 = 1 + j0 = 1 Ом;
Y 0 = 1/ Z 0 = 1/1 = 1 См.
Напряжение смещения нейтрали по (4.4.1)
а) при наличии нулевого провода
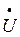 0 = ( 380 е
0 = ( 380 е 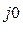 0, 1 е
0, 1 е 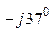 + 380 е
+ 380 е 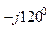 0, 1 е
0, 1 е 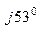 + 380 е
+ 380 е 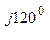 0, 0362 е
0, 0362 е 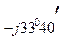 ) /
) /
/( 0, 08 – j0, 06 + 0, 06 + j0, 08 + 0, 03 – j0, 02 + 1) = (38 е 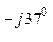 + 38 е
+ 38 е 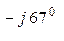 +
+
+ 13, 7е 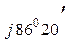 ) / 1, 17 = 32, 48 е
) / 1, 17 = 32, 48 е 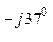 + 32, 48 е
+ 32, 48 е 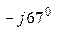 + 11, 75 е
+ 11, 75 е 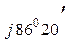 = = 26 – j19, 5 +12, 7 – j30 + 0, 752 + j11, 75 = 39, 45 – j37, 75 = 54 е
= = 26 – j19, 5 +12, 7 – j30 + 0, 752 + j11, 75 = 39, 45 – j37, 75 = 54 е 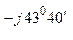 .
.
б) при обрыве нулевого провода
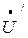 0= ( 380е
0= ( 380е 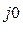 0, 1 е
0, 1 е 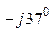 + 380е
+ 380е 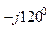 0, 1 е
0, 1 е 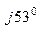 + 380е
+ 380е 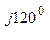 0, 0362 е
0, 0362 е 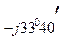 ) /
) /
/( 0, 08 – j0, 06 + 0, 06 + j0, 08 + 0, 03 – j0, 02) = (38 е 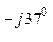 + 38 е
+ 38 е 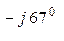 +
+
+ 13, 7 е 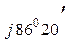 ) / 0, 17 = 223, 5 е
) / 0, 17 = 223, 5 е 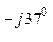 + 223, 5 е
+ 223, 5 е 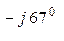 + 80, 9 е
+ 80, 9 е 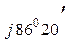 =
=
= 178 – j134 + 87 – j205 + 5, 17 + j80, 74 = 270 – j258 = 372е 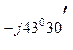 .
.
2) Определение фазных напряжений нагрузки
Напряжение на каждой фазе нагрузки  нагр. является разностью фазного напряжения источника питания
нагр. является разностью фазного напряжения источника питания  и напряжения смещения нейтрали
и напряжения смещения нейтрали 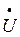 0
0
 нагр. =
нагр. =  -
- 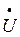 0 (4.4.3)
0 (4.4.3)
Напряжения на фазах нагрузки
а) при наличии нулевого провода
 А нагр.=
А нагр.=  А -
А -  0 = 380 - 39, 45 + j37, 75 = 340, 5 + j37, 75 = 348 е
0 = 380 - 39, 45 + j37, 75 = 340, 5 + j37, 75 = 348 е 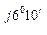 В;
В;
 В нагр. =
В нагр. =  В -
В -  0= -190 – j328 - 39, 45 + j37, 75= -229, 45 - j290, 25=370е
0= -190 – j328 - 39, 45 + j37, 75= -229, 45 - j290, 25=370е 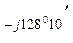 В;
В;
 С нагр.=
С нагр.=  С -
С -  0 = -190 + j328 - 39, 45 + j37, 75 = -229, 45 + j365, 75=433 е
0 = -190 + j328 - 39, 45 + j37, 75 = -229, 45 + j365, 75=433 е 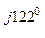 В.
В.
б) при обрыве нулевого провода

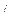 А нагр. =
А нагр. =  А -
А - 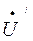 0 = 380 - 270 + j258 = 110 + j258 = 280 е
0 = 380 - 270 + j258 = 110 + j258 = 280 е 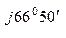 В;
В;

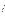 В нагр. =
В нагр. =  В -
В - 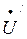 0 = -190 – j328 - 270 + j258 = - 460 – j70 = 464 е
0 = -190 – j328 - 270 + j258 = - 460 – j70 = 464 е 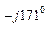 В;
В;

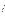 С нагр. =
С нагр. =  С -
С - 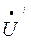 0 = -190 + j 328 - 270 + j258 = - 460 + j586 = 745 е
0 = -190 + j 328 - 270 + j258 = - 460 + j586 = 745 е 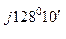 В.
В.
3) Определение фазных и линейных токов, тока в нулевом проводе
При соединении звездой фазные и линейные токи равны, т.е. Iф.А = Iл.А;
Iф.В = Iл.В; Iф.С = Iл.С;
Если известны напряжения  и проводимости Y участков, токи через них
и проводимости Y участков, токи через них
можно определить по закону Ома
 =
=  Y (4.4.4)
Y (4.4.4)
а) Фазные и линейные токи при наличии нулевого провода
 ф.А =
ф.А =  л.А =
л.А =  А нагр. Y А = 348 е
А нагр. Y А = 348 е 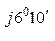 0, 1 е
0, 1 е 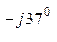 = 34, 8 е
= 34, 8 е 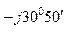 =
=
= (30 – j17, 8) А;
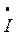 ф.В =
ф.В =  л.В =
л.В =  В нагр. Y В = 370 е
В нагр. Y В = 370 е 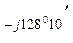 0, 1 е
0, 1 е 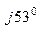 = 37 е
= 37 е 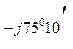 =
=
= (9, 35 – j35, 7) А;
 ф.С =
ф.С =  л.С =
л.С =  С нагр. Y С = 433 е
С нагр. Y С = 433 е 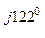 0, 0362 е
0, 0362 е 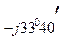 = 15, 7 е
= 15, 7 е 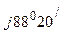 =
=
= (0, 45 + j15, 6) А
Ток в нулевом проводе
 0 =
0 =  0 Y 0 = 54 е
0 Y 0 = 54 е 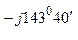 1 = 54 е
1 = 54 е 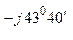 А.
А.
Этот же ток может быть найден по второму закону Кирхгофа
 0 =
0 =  ф.А +
ф.А +  ф.В +
ф.В +  ф.С = 30 – j17, 8 + 9, 35 – j35, 7 + 0, 45 + j15, 6 = 39, 8 - j37, 9 = 54 е
ф.С = 30 – j17, 8 + 9, 35 – j35, 7 + 0, 45 + j15, 6 = 39, 8 - j37, 9 = 54 е 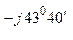 А.
А.
Совпадение результатов подтверждает правильность выполнения расчетов.
б) Фазные и линейные токи при обрыве нулевого провода
 ф.А =
ф.А = 
 л.А =
л.А =  А нагр. Y А = 280 е
А нагр. Y А = 280 е 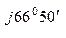 0, 1 е
0, 1 е 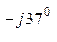 = 28 е
= 28 е 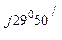 =
=
= (24, 2 + j13, 95) А;
 ф.В =
ф.В = 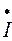
 л.В =
л.В =  В нагр. Y В =464е
В нагр. Y В =464е 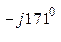 0, 1 е
0, 1 е 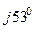 = 46, 4 е
= 46, 4 е 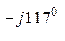 =
=
(- 21, 9 – j40, 9) А;
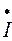
 ф.С =
ф.С = 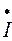
 л.С =
л.С =  нагр. Y С = 745 е
нагр. Y С = 745 е 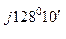 0, 0362 е
0, 0362 е 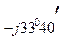 = 27 е
= 27 е 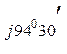 =
=
= (- 2, 3 + j26, 95) А
Ток в нулевом проводе
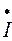 0 =
0 = 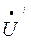 0 Y 0 = 0, т.к. при обрыве нулевого провода его проводимость равна
0 Y 0 = 0, т.к. при обрыве нулевого провода его проводимость равна
нулю.
4а) Определение мощностей
Полные мощности фаз Sф. находятся как произведение комплексов фазных напряжений  ф. на сопряженные комплексы фазных токов
ф. на сопряженные комплексы фазных токов 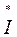 ф.
ф.
S =  ф.
ф. 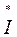 ф. (4.4.5)
ф. (4.4.5)
Сопряженный комплекс какой-либо величины – комплекс этой величины, в котором знак мнимой части заменен на противоположный.
Например: для комплекса фазного тока 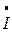 ф.В = 9, 35 – j35, 7 = 37 е
ф.В = 9, 35 – j35, 7 = 37 е 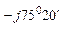 его сопряженный комплекс имеет вид:
его сопряженный комплекс имеет вид: 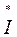 ф.В = 9, 35 + j35, 7 = 37 е
ф.В = 9, 35 + j35, 7 = 37 е 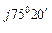 А.
А.
Сопряженные комплексы величин принято обозначать звездочками над их буквенными символами.
Полная мощность каждой фазы по (4.4.5)
S А=  А
А 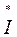 ф.А = 348 е
ф.А = 348 е 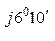 34, 8 е
34, 8 е 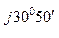 = 11696 е
= 11696 е 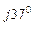 = (9357 + j7017) ВА;
= (9357 + j7017) ВА;
S В=  В
В 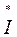 ф.В = 370 е
ф.В = 370 е 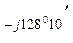 37 е
37 е 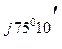 = 13690 е
= 13690 е 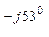 = (8214 – j10952) ВА;
= (8214 – j10952) ВА;
S С=  С
С 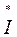 ф.С = 433 е
ф.С = 433 е 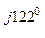 15, 7 е
15, 7 е 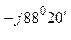 = 6785 е
= 6785 е  = (5647 + j3757) ВА.
= (5647 + j3757) ВА.
Полная мощность всей нагрузки
S = S А+ S В+ S С = 9357 + j7017 + 8214 – j10952 + 5647 + j3757 = (23218 – j178)ВА.
Активная и реактивная мощности фаз и всей нагрузки находятся как действительная и мнимая части соответствующих комплексов полных мощностей, т.е.
активная мощность фаз
РА = 9357 Вт;
РВ = 8214 Вт;
РС = 5647 Вт;
активная мощность всей нагрузки
Р = РА + РВ + РС = 9357 + 8214 + 5647 = 23218 Вт;
реактивная мощность фаз
QА = 7017 вар;
QВ = -10952 вар;
QС = 3757 вар;
реактивная мощность всей нагрузки
Q = QА + QВ + QС = 7017 -10952 + 3757 = -178 вар.
Активная мощность каждой фазы может быть также найдена по выражению
Рф. = I 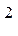 ф. Rф., (4.4.6)
ф. Rф., (4.4.6)
где Iф. – действующее значение фазного тока;
Rф. – активное сопротивление фазы.
Тогда
РА = I 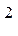 ф.А Rф.А =(34, 8)
ф.А Rф.А =(34, 8) 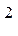 8 = 9357 Вт;
8 = 9357 Вт;
РВ = I 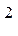 ф.В Rф.В = (37)
ф.В Rф.В = (37) 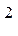 6 = 8214 Вт;
6 = 8214 Вт;
РС = I 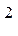 ф.С Rф.С = (15, 7)
ф.С Rф.С = (15, 7) 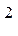 23 = 5647 Вт.
23 = 5647 Вт.
4б) Определение коэффициентов мощности
Коэффициент мощности сos 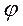 является отношением действительных частей комплексов полной мощности или полного сопротивления к их модулям
является отношением действительных частей комплексов полной мощности или полного сопротивления к их модулям
сos 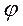 = a/А, (4.4.7)
= a/А, (4.4.7)
где а – действительная часть комплекса;
А – модуль величины.
Таким образом, коэффициенты мощности фаз, найденные с использованием различных величин, при правильном решении должны совпасть.
Коэффициенты мощности фаз
сos 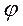 А = РА/SА = 9357/11696 = 0, 8, или сos
А = РА/SА = 9357/11696 = 0, 8, или сos 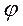 А = RА/ZА = 8/10 = 0, 8
А = RА/ZА = 8/10 = 0, 8
сos 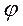 В = РВ/SВ = 8214/13690 = 0, 6, или сos
В = РВ/SВ = 8214/13690 = 0, 6, или сos 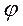 В = RВ/ZВ = 6/10 = 0, 6
В = RВ/ZВ = 6/10 = 0, 6
сos 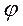 С = РС/SС = 5647/6785 = 0, 8323, или сos
С = РС/SС = 5647/6785 = 0, 8323, или сos 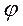 С = RС/ZС = 23/27, 6 = 0, 8333
С = RС/ZС = 23/27, 6 = 0, 8333
(Несовпадение значений сos 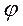 С в третьем знаке вызвано округлением чисел при расчетах).
С в третьем знаке вызвано округлением чисел при расчетах).
Средний коэффициент мощности нагрузки находится по мощности всей цепи
сos 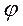 нагр. ср. = Р/S = 23218 /
нагр. ср. = Р/S = 23218 / 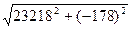 = 23218/23218, 7 =1, 0
= 23218/23218, 7 =1, 0
Полученные при расчете данные сведены в таблицу 8.
Таблица 8 - Результаты расчета трехфазной четырехпроводной цепи
| Режим работы цепи | Величина | Комплекс величины | Действующее значение | |
| В алгебраической форме | В показательной форме | |||
| Нулевой провод исправен | Напряжение смещения нейтрали  0, В 0, В
| 39, 45 – j37, 75 | 54 е 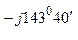
| |
| Фазные напряжения, В |  А нагр. А нагр.
| 340, 5 + j37, 75 | 348 е 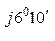
| |
 В нагр. В нагр.
| -229, 45 - j290, 25 | 370 е 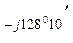
| ||
 С нагр. С нагр.
| -229, 45+ j365, 75 | 433 е 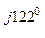
| ||
| Фазные (линейные) токи, А |  ф.А = ф.А =  л.А л.А
| 30 – j17, 8 | 34, 8 е 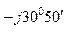
| 34, 8 |
 ф.В = ф.В =  л.В л.В
| 9, 35 – j35, 7 | 37 е 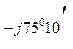
| ||
 ф.В = ф.В =  л.В л.В
| 9, 35 – j35, 7 | 37 е 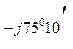
|
Продолжение таблицы 8
| Нулевой провод исправен | Ток в нулевом проводе  0, А 0, А
| 39, 45 – j37, 75 | 54 е 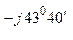
| |
| Полная мощность фаз, ВА | S А | 9357 + j7017 | 11696 е 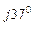
| |
| S В | 8214 – j10952 | 13690 е 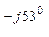
| ||
| S С | 5647 + j3757 | 6785 е 
| ||
| Полная мощность цепи S, ВА | 23218 – j178 | 23178 е 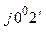
| ||
| Активная мощность фаз, Вт | РА | - | - | |
| РВ | - | - | ||
| РС | - | - | ||
| Активная мощность цепи Р, Вт | - | - | ||
| Реактивная мощность фаз, вар | QА | - | - | |
| QВ | - | - | -10952 | |
| QС | - | - | ||
| Реактивная мощность цепи Q, вар | - | - | -178 | |
| Коэффициенты мощности фаз | сos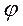 А А
| - | - | 0, 8 |
сos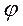 В В
| - | - | 0, 6 | |
сos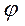 С С
| - | - | 0, 8323 | |
Средний коэффициент мощности цепи сos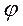
| - | - | 1, 0 |
Продолжение таблицы 8
| Нулевой провод оборван | Напряжение смещения нейтрали 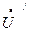 0, В 0, В
| 270 – j258 | 372е 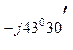
| |
| Фазные напряжения, В |  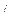 А нагр. А нагр.
| 110 + j258 | 280 е 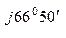
| |
 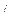 В нагр. В нагр.
| -460 – j70 | 464 е 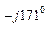
| ||
 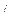 С нагр. С нагр.
| -460 + j586 | 745 е 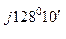
| ||
| Фазные (линейные) токи, А | 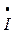  ф.А = ф.А = 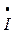  л.А л.А
| 24, 2 + j13, 95 | 28 е 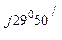
| |
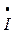  ф.В = ф.В = 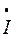  л.В л.В
| - 21, 9 – j40.9 | 46, 4 е 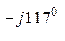
| 46, 4 | |
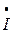  ф.С = ф.С =   л.С л.С
| - 2, 3 + j26, 95 | 27 е 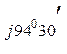
| ||
Ток в нулевом проводе   0, А 0, А
|