
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методический материал
|
|
Практическое занятие 2-3
Функции многих переменных
Дифференциал. Частные производные высших порядков
Методический материал
1) Найти частные производные функции
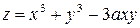 .
.
Вычислить их значения в точке 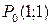 .
.
Решение. Считается  постоянным, находим
постоянным, находим 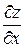 :
:
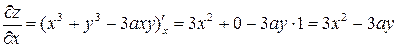 .
.
При нахождении  фиксируется аргумент
фиксируется аргумент  , т.е.
, т.е.
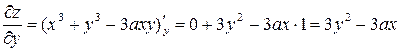 .
.
Значения производных в точке 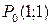 следующее:
следующее:
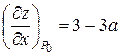 ;
; 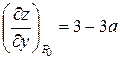 .
.
2) Найти значения частных производных в точке 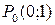 функции
функции 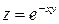 .
.
Решение. Находим частные производные, используя формулу дифференцирования сложной функции 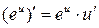
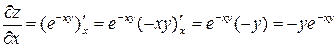 ;
;
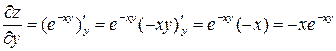 .
.
Подставляя координаты точки 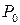 , получим
, получим 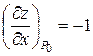 ,
, 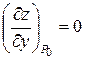 .
.
14) Найти 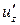 , если
, если 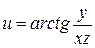 .
.
Решение. По правилу дифференцирования сложной функции, считая 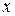 и
и 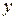 постоянными, получим
постоянными, получим
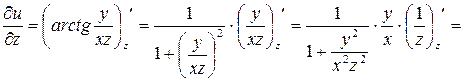
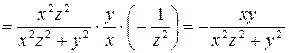 .
.
3) Доказать, что функция 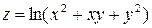 удовлетворяет уравнению
удовлетворяет уравнению
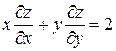 .
.
Решение. Находим частные производные:
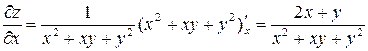 ;
;
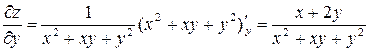 .
.
Подставляя 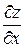 и
и 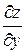 в данное уравнение:
в данное уравнение:
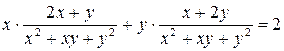 ,
, 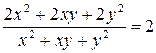 , 2=2;
, 2=2;
полученное тождество показывает, что функция удовлетворяет данному уравнению.
4) Найти вторые частные производные функции  .
.
Решение. Находим первые производные:
 ,
,
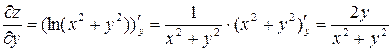 .
.
Дифференцируя каждую из полученных производных по 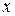 и по
и по 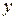 , получим вторые частные производные:
, получим вторые частные производные:
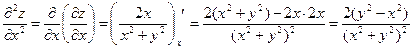 ,
,
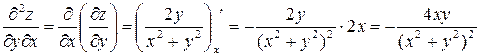 ,
,
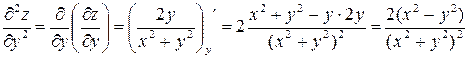 .
.
Функция  непрерывна в любой точки плоскости
непрерывна в любой точки плоскости  , кроме точки
, кроме точки 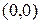 , и в каждой точки непрерывности выполняется равенство
, и в каждой точки непрерывности выполняется равенство
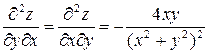 ..
..
5) Найти 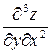 , если
, если 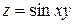 .
.
Решение. Дифференцируем данную функцию по 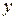 и затем дважды по
и затем дважды по 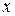 :
:
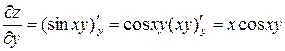 ,
,
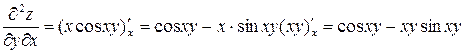 ,
,
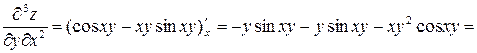
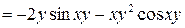 .
.
6) Найти полный дифференциал функции 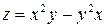 .
.
Решение. Находим частные производные:
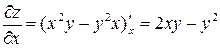 ;
; 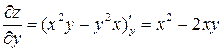 .
.
По формуле 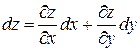 имеем
имеем
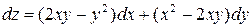 .
.
Полный дифференциал можно найти также и по другому, используя правила дифференцирования:
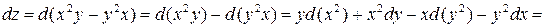
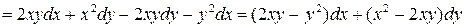 .
.
7) Найти  , если
, если 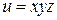 .
.
Решение. Для данной функции
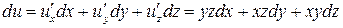 ,
,
поэтому 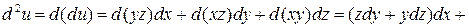
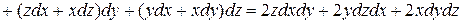 .
.
8) Высота конуса Н=10см, радиус основания 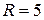 см. Как изменится объем конуса при увеличении высоты на 2мм и уменьшении радиуса основания на 2мм?
см. Как изменится объем конуса при увеличении высоты на 2мм и уменьшении радиуса основания на 2мм?
Решение. Объем конуса 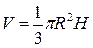 . Изменение объема
. Изменение объема 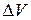 приближенно заменим его дифференциалом
приближенно заменим его дифференциалом
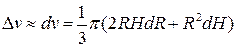 .
.
Подставив значения (в см) 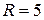 ,
, 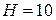 ,
, 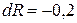 ;
; 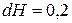 ,
,
получим
 .
.
Таким образом, объем конуса уменьшится примерно на 15, 7 см  .
.
9) Вычислить приближенно число 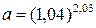 .
.
Решение. Рассмотрим функцию 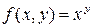 . Данное число
. Данное число 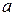 есть приращенное значение этой функции в точке
есть приращенное значение этой функции в точке 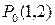 при
при 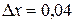 ,
, 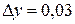 .
.
Дифференциал данной функции
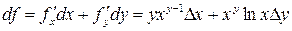 .
.
Его значение в точке 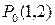 при данных приращениях
при данных приращениях
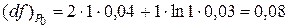 ,
,
поэтому 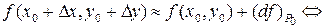
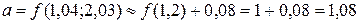 .
.