
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 1. По семи территориям Уральского района за 2002 г
|
|
По семи территориям Уральского района за 2002 г. известны значения двух признаков (табл. 1.1).
Таблица 1.1
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68, 8 | 45, 1 |
| Свердловская обл. | 61, 2 | 59, 0 |
| Башкортостан | 59, 9 | 57, 2 |
| Челябинская обл. | 56, 7 | 61, 8 |
| Пермская обл. | 55, 0 | 58, 8 |
| Курганская обл. | 54, 3 | 47, 2 |
| Оренбургская обл. | 49, 3 | 55, 2 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы.
2. Оценить каждую модель через среднюю ошибку аппроксимации 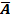 и F -критерий Фишера.
и F -критерий Фишера.
Решение:
1а. Для расчета параметров a и b линейной регрессии 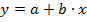 решаем систему нормальных уравнений относительно а и b:
решаем систему нормальных уравнений относительно а и b:
По исходным данным рассчитываем: 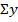 ,
, 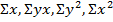
Таблица 1.2
| y | х | ух | x2 | y2 | 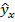
| 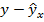
| Ai | |
| 68, 8 | 45, 1 | |||||||
| 61, 2 | 59, 0 | |||||||
| 59, 9 | 57, 2 | |||||||
| 56, 7 | 61, 8 | |||||||
| 55, 0 | 58, 8 | |||||||
| 54, 3 | 47, 2 | |||||||
| 49, 3 | 55, 2 | |||||||
| Итого | 405, 2 | 384, 3 | ||||||
| Среднее значение | 57, 89 | 54, 90 | ||||||
| σ | 5, 74 | 5, 86 | - | - | - | - | - | - |
| σ 2 | 32, 92 | 34, 34 | - | - | - | - | - | - |
Уравнение регрессии: __________________________
Интерпретация уравнения регрессии: С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров __________ в среднем на _______%-ных пункта.
Рассчитаем линейный коэффициент парной корреляции:
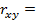
Вывод: Связь _______________.
Определим коэффициент детерминации:
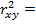
Вывод: Вариация результата на _________% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения 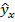 . Найдем величину средней ошибки аппроксимации
. Найдем величину средней ошибки аппроксимации 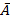 :
:

Вывод: В среднем расчетные значения отклоняются от фактических на ______%.
Рассчитаем F -критерий:
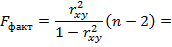
Вывод: Полученное значение указывает на необходимость ____________ гипотезу Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
1б. Построению степенной модели 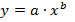 предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
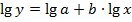
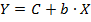
где 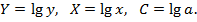
Расчеты можно вести в табл. 1.3.
Таблица 1.3
| Y | X | YX | Y2 | X2 | 
| 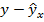
| 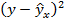
| Ai | |
| Итого | |||||||||
| Среднее значение | - | - | |||||||
| σ | - | - | - | - | - | - | - | ||
| σ 2 | - | - | - | - | - | - | - |
Рассчитаем C и b:
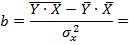
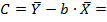
Получим линейное уравнение: ___________________.
Выполнив его потенцирование, получим:
_____________________________________________
Подставляя в данное уравнение фактические значения x, получаем теоретические значения результата 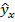 . По ним рассчитаем показатели: тесноты связи - индекс корреляции
. По ним рассчитаем показатели: тесноты связи - индекс корреляции 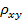 и среднюю ошибку аппроксимации
и среднюю ошибку аппроксимации 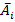 :
:
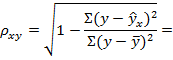
 =
=
Вывод: Характеристики степенной модели указывают, что она ____________________линейной функции описывает взаимосвязь.
1в. Построению уравнения показательной кривой  предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
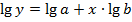
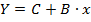
где 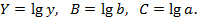
Расчеты можно вести в табл. 1.4.
Таблица 1.4
| Y | х | Yх | Y2 | X2 | 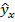
| 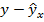
| 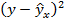
| Ai | |
| Итого | |||||||||
| Среднее значение | - | - | |||||||
| σ | - | - | - | - | - | - | - | ||
| σ 2 | - | - | - | - | - | - | - |
Значения параметров регрессии А и В составили:
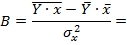
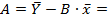
Получим линейное уравнение: ____________________. Произведем потенцирование полученного уравнения и запишем его в обычной форме:
_____________________________________.
Тесноту связи оценим через индекс корреляции ρ ху
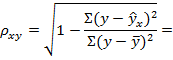
Вывод: Связь _____________.
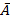 = ______%, что говорит о ___________ ошибке аппроксимации, но в допустимых пределах.
= ______%, что говорит о ___________ ошибке аппроксимации, но в допустимых пределах.
Вывод: Показательная функция _________, чем степенная описывает изучаемую зависимость.
1г. Уравнение равносторонней гиперболы 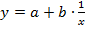
линеаризуется при замене: 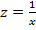 . Тогда
. Тогда 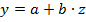 .
.
Расчеты можно вести в табл. 1.5.
Таблица 1.5
| y | z | yz | z2 | y2 | 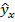
| 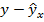
| 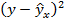
| Ai | |
| Итого | |||||||||
| Среднее значение | - | - | |||||||
| σ | - | - | - | - | - | - | - | ||
| σ 2 | - | - | - | - | - | - | - |
Значения параметров регрессии a и b составили:
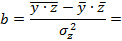
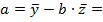
Получим уравнение: ____________________________
Индекс корреляции:
ρ ху=
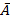 = ______%,
= ______%,
По уравнению равносторонней гиперболы получена ___________ оценка тесноты связи: рху = ________ (по сравнению с линейной, степенной и показательной регрессиями). 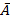 остается на ____________ уровне.
остается на ____________ уровне.
2. Рассчитаем Fфакт=
Сравним его с Fтабл=
Вывод:
|