Расчет долговечности подшипников качения трансмиссии машины.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N 8

Расчет долговечности подшипников качения трансмиссии машины.

.

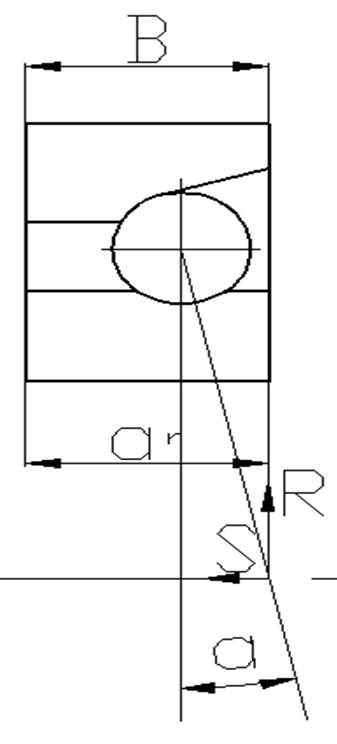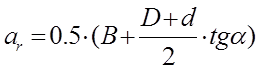
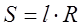
B-ширина подшипника, D-наружный диаметр, в d-внутренний диаметр

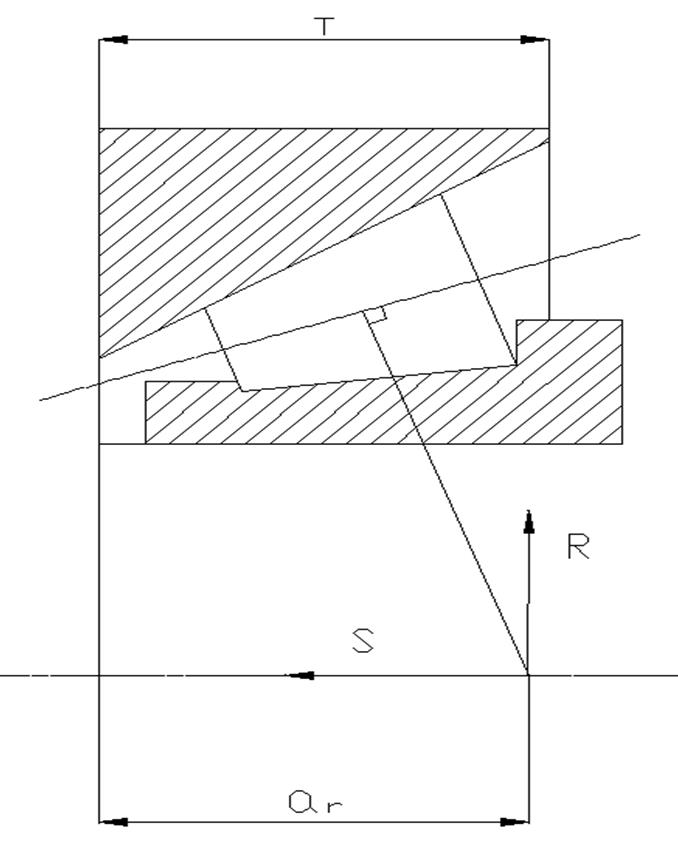
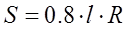T-ширина обоймы

Условия нагружения Опора 1 Опора 2

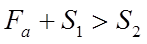
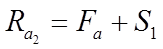
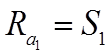
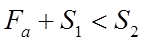
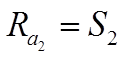
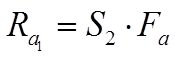
ГОСТ 18855-94 (UCO 281-89)

Шариковый радиальный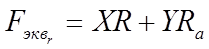

Шариковый радиальный упорный

Роликовый радиальный упорный

Роликовый радиальный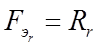

Шариковый и роликовый упорные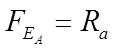

Шариковый и роликовый упорно-радиальные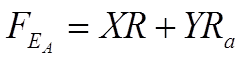

Приведенная нагрузка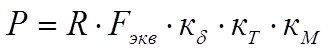

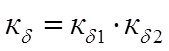-коэффициент безопасности, где

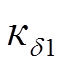-внутренняя динамическая нагрузка, 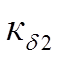- внешняя динамическая нагрузка;

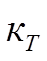-коэффициент температуры, 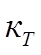=1 если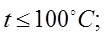

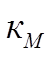-коэффициент материала, 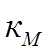=1 если .

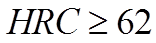Долговечность 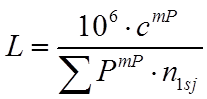(в километрах пробега), где

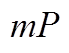=3 для шариковых, 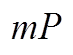=3, 33 для роликовых, 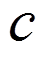-динамическая грузоподъемность, 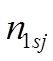-число оборотов за 1 км пробега.

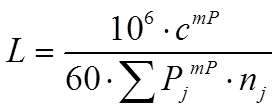(в часах), 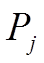- число передач.

2. Работа ведущего колеса.

Общий случай. Рассмотрим неравномерное движение ведущего колеса по горизонтальной деформируемой поверхности (рисунок 2.16). В соответствии со схемой качение колеса вызывается ведущим моментом 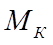, приложенным к его оси. Со стороны остова трактора на колесо действуют: реактивная сила 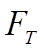, пред­ставляющая собой сопротивление, оказываемое остовом машины толкающему ее колесу, и вертикальная нагрузка G, включающая часть веса остова, приходящегося на колесо, и вес колеса. Реак­тивные силы, действующие со стороны грунта на колесо, пред­ставлены равнодействующей R, которая приложена в точке Aопорной поверхности колеса.

Рисунок 2.16. Схема сил и моментов, действующих на ведущее колесо, оборудованное шиной.

При неравномерном относительном вращении колеса около его оси возникает также момент касательных сил инерции 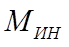равный произведению момента инер­ции колеса J относительно его гео­метрической оси на угловое ускорение (замедление) 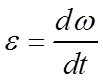относи­тельно вращательного движения.

При неравномерном переносном движении колеса возникают силы инерции, направленные против дви­жения (при ускоренном движении) и параллельные поверхности пути. Равнодействующая сил инерции 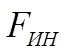равна произведению массы т на ускорение .

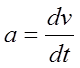Разложим равнодействующую реакций грунта на вертикальную составляющую Yи горизонтальную составляющую X.Вер­тикальная составляющая Yпредставляет собой сумму элементар­ных нормальных реакций грунта, а горизонтальная составля­ющая X - сумму тангенциальных реакций грунта, направленных в сторону движения. Иногда Xназывают толкающей силой или толкающей реакцией.

В связи с деформациями почвы и радиальными деформациями шины, происходящими при движении колеса, вертикальная реак­ция почвы Y смещается относительно оси колеса вперед на не­которое расстояние с.

Воспользуемся принципом Д'Аламбера и составим следующие уравнения для плоской модели колеса:

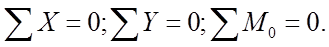(2.27) (2.28) (2.29)

Из уравнений (2.27)—(2.29) имеем

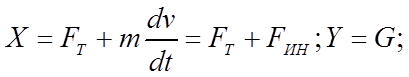
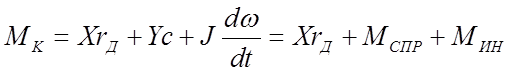(2.30)

Где 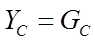- момент сил сопротивления качению ведущего колеса М_спр вследствие образования колеи; с— коэффициент трения качения ведущего колеса, который измеряется в единицах длины; 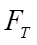- реактивная сила.

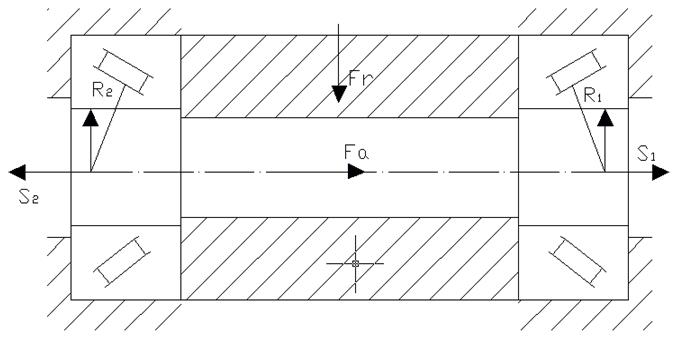
При установившемся движении 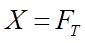, т. е. сумма танген­циальных реакций почвы, возникающих при взаимодействии ведущего колеса с грунтом, равна реактивной силе 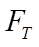, и 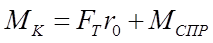, т. е. подводимый к колесу ведущий момент равен сумме моментов силы сопротивления остова машины толкающему ее колесу и момента сопротивления вследствие образования колеи.

Разделим обе части уравнения (2.30) на динамический радиус колеса:

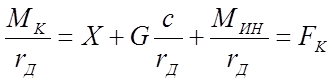
Отношение 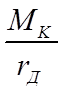назовем касательной силой тяги, а отно­шение коэффициента трения качения с к динамическому ра­диусу - коэффициентом качения ведущего колеса, т. е. .

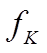Отношение касательной силы тяги колеса к вертикальной нагрузке назовем коэффициентом сцепления.

Соответственно 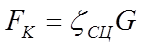. При качении ведущего колеса по грунту коэффициент сцепления всегда меньше единицы. Сле­довательно, максимальная касательная сила тяги колеса всегда меньше веса, приходящегося на него.

Произведем оценку баланса мощности, подводимой к веду­щему колесу при качении его по деформируемой поверхности. Умножая обе части уравнения моментов на угловую скорость колеса, получаем следующий баланс мощностей:

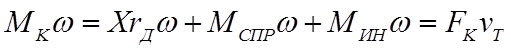(2.31)

Как было установлено ранее, качение ведущего колеса по грунту всегда сопровождается его буксованием, что характери­зуется уменьшением скорости в переносном движении, и дей­ствительная скорость движения колеса теоретическая скорость движения, равная произве­дению угловой скорости на радиус качения (кинематический). С некоторым приближением можно заменить кинематический радиус динамическим. Тогда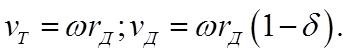

Имея в виду это обстоятельство, учтем пробуксовку колеса, для чего в уравнение (2.31) добавим и отнимем сумму членов, отражающих переносное поступательное движение, умноженных на действительную поступательную скорость

.

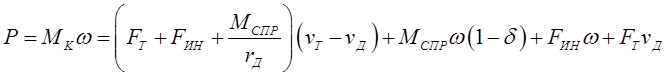Следовательно, мощность, сообщаемая ведущему колесу, в рас­сматриваемом случае равна сумме следующих мощностей:

1) теряемой на буксование колеса расходуемой на качение колеса, т. е. на образование колеи и упругий гистерезис шины превращаемой в кинетическую энергию переносного посту­пательного движения превращаемой в кинетическую энергию вращательного дви­жения колеса около его оси передаваемой остову трактора.

При установившемся движении баланс мощности имеет вид:

.
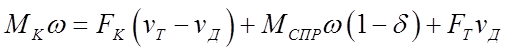