Основные типы данных

Основной объект системы MatLab - прямоугольный числовой массив (матрица), в котором допускается применение комплексных элементов. Использование матриц не требует явного указания их размеров.

Большинство операций и функций реализовано таким образом, что их аргументами могут быть как скалярные величины, так и матрицы. При этом результат выполнения операции также будет скалярным или матричным, в зависимости от аргумента. Матрицы в MatLab записываются перечислением своих элементов внутри квадратных скобок по строкам, строки при этом разделяются точками с запятой. Рассмотрим пример – сложение двух матриц, которое выполняется по аналогии со сложением двух скалярных величин:

> > A=[1 2; 3 4];

> > B=[8 7; 6 5];

> > C=A+B

C=

9 9

9 9

Знак “+” означает матричное сложение, то есть аргументы складываются по правилам матричной алгебры. То же самое касается операций вычитания, умножения и деления – эти операции выполняются по правилам матричной алгебры, которые в случае скалярных аргументов совпадают с правилами обычных арифметических вычислений. Размеры матриц аргументов при этом должны быть согласованы по правилам линейной алгебры. Для выполнения операции над матричными аргументами поэлементно следует использовать поэлементные операции: “.+”, “.-“, “.*”, “./”. Результатом поэлементной операции будет матрица, все элементы которой являются результатом этой операции над соответствующими элементами аргументов. Для операций сложения и вычитания матричные операции совпадают с поэлементными операциями, но для умножения, деления и возведения в степень (которое записывается как x^n) это уже не так:

> > A=[1 2; 3 4];

> > B=[8 7; 6 5];

> > C=A*B

C=

20 17

48 41

> > D=A.*B

D =

8 14

18 20

Матричное деление матрицы A на матрицу B в MatLab понимается как нахождение такой матрицы C=A/B, чтобы матрица C*B-A была бы наиболее близка к нулевой матрице в смысле некоторой нормы.

Ещё одна матричная операция, а именно транспонирование, записывается в MatLab так:

> > A.’

Если в этой записи точку перед апострофом не ставить, то вдобавок к транспонированию все элементы матрицы будут взяты с комплексным сопряжением. Здесь заметим, что комплексные числа используются в системе MatLab, и над ними можно производить все определённые для них вычисления. Комплексное число представляется как сумма действительной и мнимой части, формируемой при помощи специальной константы – мнимой единицы, которая после начала работы системы помещается одновременно в две ячейки – переменные i и j. Присваивать другие значения этим переменным можно, но не рекомендуется.

Простейшая операция над комплексными числами – выделение действительной и мнимой части – показана на примере, дополнительно иллюстрирующем, что многие функции в MatLab могут принимать и возвращать как скалярные, так и матричные значения.

> > A=[2+3*i 1-7*j -4*i];

> > Re=real(A)

Re=

[2 1 0]

> > Im=imag(A)

Im=

[3 -7 -4]

Ещё одно полезное качество системы MatLab – возможность возвращать несколько результатов из одного вызова функции. Причём пользователь может сам определять, нужно ли ему получать все результаты или нет. Например, функции min и max могут возвращать не только минимальный или максимальный элемент вектора, но и его индекс (номер позиции в векторе):

> > a=[4 3 2 75 2];

> > max (a)

ans =

> > [m idx]=min(a)

m=

idx=

Если вызов функции производится без присваивания какой-либо переменной, то ответ помещается в специальную переменную ans, при этом она получает значение только первого из возвращаемых параметров. Чтобы получить значения остальных выходных параметров, необходимо в операторе присваивания зарезервировать под них переменные, как это показано в примере. Полученное значение индекса наименьшего элемента можно использовать для выбора соответствующего элемента из вектора. В общем случае запись 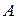A(m, n) означает выбор одного из элементов прямоугольной матрицы, стоящего на пересечении строки m и столбца n, а запись A(k) – выбор элемента, находящегося на позиции k из вектора, полученного записыванием по очереди всех столбцов матрицы в один вектор. Если же необходимо вычленить из матрицы A подматрицу, находящуюся на пересечении строк с i0 по i1 и столбцов с j0 по j1, то это можно сделать так: A(i0: i1, j0: j1). Запись i0: i1 означает вектор целых чисел от i0 до i1. Имеет место следующее обобщение: запись a0: a1: a2 в MatLab означает упорядоченный набор чисел, начинающийся с числа a0, образующих арифметическую прогрессию с шагом a1 и не превосходящих величину a2 (с нужной стороны, в зависимости от знака a1).

Ещё одно замечание – по умолчанию любая команда в системе MatLab приводит к отображению результата. Чтобы результат не выводился, достаточно завершить ввод команды точкой с запятой:

> > a=[1 2; 3 4]

a=

1 2

3 4

> > a;

> > b=[1 2; 3 4];

> > b

b=

1 2

3 4

Это полезно при создании пользователем функций в режиме программирования, когда в процессе расчёта по программе необходимо избежать вывода результатов промежуточных вычислений.

Единичная матрица, то есть матрица имеющая единицы на главной диагонали и нулевые ос-тальные элементы, в MatLab обозначается eye, причем eye(n) есть единичная квадратная матрица размера nxn, eye(m, n) - прямоугольная единичная матрица размера mxn, а eye(size(A)) есть единичная матрица, имеющая размерность матрицы A. Например,

I = eye(3) I = eye (3, 5) I = eye (4, 2 )

I = I = I =

1 0 0 1 0 0 0 0 1 0

0 1 0 0 1 0 0 0 0 1

0 0 1 0 0 1 0 0 0 0

0 0

Нулевая матрица, то есть матрица состоящая из нулей (массив нулей), в MatLab обозначается zeros, причем zeros (n) есть нулевая квадратная матрица размера nxn, zeros (m, n) - прямоугольная нулевая матрица размера mxn, а zeros (size(A)) есть нулевая матрица имею-щая размерность матрицы A.

Z = zeros(2, 4)

Z =

0 0 0 0

0 0 0 0

Наконец, матрица состоящая из единиц (массив единиц), в MatLab обозначается ones, причем ones (n) есть квадратный массив единиц размера nxn, ones (m, n) – прямоугольный массив единиц размера mxn, а ones (size(A)) есть массив единиц, имеющий размерность матрицы A.

S = 5*ones(3, 3)

S =

5 5 5

5 5 5

5 5 5

Аналогично, функция rand дает возможность сформировать соответствующие массивы случайных чисел в диапазоне от 0 до 1, распределенных по равномерному закону, а функция randn – по нормальному закону.

N = fix(10*rand(1, 10))

N =

4 9 4 4 8 5 2 6 8 0

R = randn(4, 4)

R =

1.0668 0.2944 -0.6918 -1.4410

0.0593 -1.3362 0.8580 0.5711

-0.0956 0.7143 1.2540 -0.3999

-0.8323 1.6236 -1.5937 0.6900