
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Продовження таблиці 1.7. – Множини А та В
|
|
| № | Множини | № | Множини |
| 7. | А={1, 5, 7, 9}; В={0, 6, 7} | 8. | А={1, 3, 4}; В={2, 4} |
| 9. | А={1, 3, 4}; В={5, 6, 3} | 10. | А={1, 2}; В={1, 2} |
| 11. | А={1, 2, 3}; В={1, 2, 3} | 12. | А={1, 4, 6}; В={1, 4, 8} |
| 13. | А={1, 8, 9}; В={6, 8} | 14. | А={1, 2, 3}; В={4, 5, 6} |
| 15. | А={4, 7, 9}; В={1, 2, 5} | 16. | А={2, 5, 8}; В={3, 6, 7} |
| 17. | А={4, 5, 8}; В={1, 2, 3, 4} | 18. | А={1, 2}; В={1, 2, 3, 4, 5} |
| 19. | А={4, 5, 7}; В={3, 5, 9} | 20. | А={1, 2}; В={1, 2, 3, 4, 8} |
| 21. | А={7, 5}; В={4, 9} | 22. | А={7, 8, 4}; В={1, 2, 3} |
| 23. | А={1, 5, 9}; В={7, 5, 3} | 24. | А={1, 2}; В={3, 5, 4} |
| 25. | А={1, 7, 4}; В={4, 7, 1} | 26. | А={2, 4, 8}; В={3, 7} |
| 27. | А={5, 8}; В={2, 5, 4} | 28. | А={1, 4}; В={1, 2, 5} |
| 29. | А={4, 7}; В={3, 5, 9} | 30. | А={0, 2}; В={1, 2, 3} |
Завдання № 1.3.2. Задано бінарне відношення R1 як перелік елементів на множині А = {1, 2, 3, 4}, R1 A2 (табл. 1.7).
Таблиця 1.7 – Бінарні відношення
| Варіант | Відношення |
| R1= {(1, 1), (1, 2), (2, 1), (2, 2), (3, 4), (4, 1), (4, 4)} | |
| R1= {(1, 1), (1, 2), (2, 1)} | |
| R1= {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (3, 3), (4, 1), (4, 4)} | |
| R1= {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)} | |
| R1= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)} | |
| R1= {(4, 3)} | |
| R1= {(3, 4)} | |
| R1= {(1, 1), (2, 2), (3, 2), (3, 3), (4, 4)} | |
| R1= {(1, 1), (1, 2), (1, 3)} | |
| R1= {(1, 1), (2, 1), (2, 2), (2, 3)} | |
| R1= {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)} | |
| R1= {(1, 3), (3, 1)} | |
| R1= {(1, 3), (1, 4), (2, 3), (2, 4), (3, 1), (3, 4)} | |
| R1= {(1, 1), (2, 2), (3, 3), (4, 4)} | |
| R1= {(1, 2), (2, 3), (3, 4)} | |
| R1= {(2, 4), (4, 2)} | |
| R1= {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (4, 4)} | |
| R1= {(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4)} | |
| R1= {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (3, 4)} |
Продовження таблиці 1.7 – Бінарні відношення
| Варіант | Відношення |
| R1= {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (4, 4)} | |
| R1= {(1, 1), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 3), (4, 4)} | |
| R1= {(1, 1), (2, 2), (3, 3), (4, 1), (4, 2), (4, 4)} | |
| R1= {(1, 1), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)} | |
| R1= {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (3, 3), (4, 1), (4, 4)} | |
| R1= {(1, 2), (1, 3), (1, 4), (2, 3), (4, 3)} | |
| R1= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (3, 1), (3, 3), (4, 1), (4, 4)} | |
| R1= {(1, 1), (1, 4), (2, 2) (2, 3), (3, 3), (4, 4)} | |
| R1= {(1, 1), (1, 4), (2, 1), (2, 2), (4, 1), (4, 4)} | |
| R1= {(2, 1), (3, 1), (3, 2), (4, 1), (4, 3)} | |
| R1= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)} |
1. Задати відношення за допомогою матриці та графа.
2. Записати властивості відношення. Перевірити, чи є відношення відношенням еквівалентності, толерантності, порядку.
3. Визначити, чи є дане відношення функціональним, відображенням. Якщо є відображенням, то визначити тип відображення. Відповідь обґрунтувати.
Завдання № 1.3.3. Аналітично довести або спростувати істинність виразу (табл. 1.8.).
Таблиця 1.8. – Тотожності
| № | Тотожність | № | Тотожність |
| 1. | 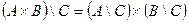
| 2. | 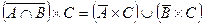
|
| 3. | 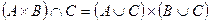
| 4. | 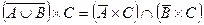
|
| 5. | 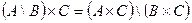
| 6. | 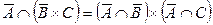
|
| 7. | 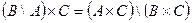
| 8. | 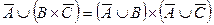
|
| 9. | 
| 10. | 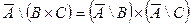
|
| 11. | 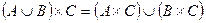
| 12. | 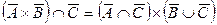
|
| 13. | 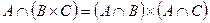
| 14. | 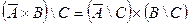
|
| 15. | 
| 16. | 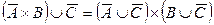
|
| 17. | 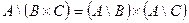
| 18. | 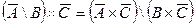
|
| 19. | 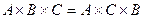
| 20. | 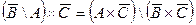
|
| 21. | 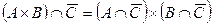
| 22. | 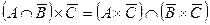
|
| 23. | 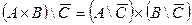
| 24. | 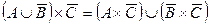
|
| 25. | 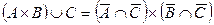
| 26. | 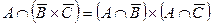
|
| 27. | 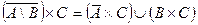
| 28. | 
|
| 29. | 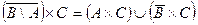
| 30. | 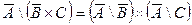
|