
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание по матем. статистике
|
|
Правила выполнения и оформления
Контрольных работ
При выполнении контрольных работ необходимо придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного.
2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер – последняя цифра в зачетке, название дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента.
3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются.
4. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
6. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
7. После получения прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
В случае незачета работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
Контрольная работа
Вариант 1
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1. Определить сходимость числового ряда 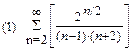
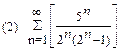

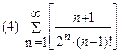
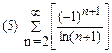
2. Найти область сходимости функционального ряда: 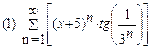
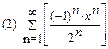
3. Разложить функцию в ряд Маклорена: (1) 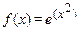 (2)
(2) 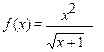 по степеням
по степеням 
Тема «Комплексные числа и теория функции комплексного переменного»
4. Вычислить и записать в алгебраической форме 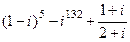 .
.
5. Решить уравнение: 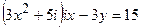 .
.
6. Вычислить и записать в тригонометрической форме 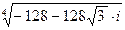
7. Изобразить область, ограниченную линиями а) 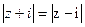 ; б)
; б) 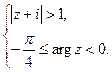
Тема «Операционное исчисление»
8. Используя теоремы линейности, смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a) 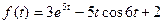 ; б)
; б) 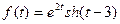 .
.
9. Найти оригинал по заданному изображению:
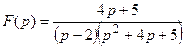
Тема «Теория вероятностей и математическая статистика»
10. Детали изготавливаются на двух станках. На первом станке - 40%, на втором - 60%. Среди деталей, изготовленных на первом станке, брак составляет 2%, на втором – 1.5%. Случайным образом взята одна деталь для контроля. Найти вероятности событий: 1) деталь бракованная; 2) деталь изготовлена на первом станке, если она при проверке оказалась без брака.
11. Вероятность появления опечатки на странице книги, содержащей 100 страниц, равна 0.03. Найти вероятность того, что в книге имеется не более двух опечаток: 1) по биномиальной формуле; 2) по формуле Пуассона.
12. СВ 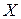 задана законом распределения. Найти: 1) числовые характеристики
задана законом распределения. Найти: 1) числовые характеристики 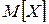 ,
, 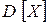 ; 2) функцию распределения
; 2) функцию распределения 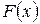 и построить ее график; 3)вероятность
и построить ее график; 3)вероятность 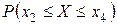 ; 4) закон распределения величины СВ
; 4) закон распределения величины СВ 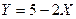 . Вычислить
. Вычислить 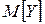 ,
, 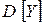 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
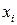
| |||||

| ? | 0, 2 | 0, 1 | 0, 2 | 0, 4 |
13. Дана плотность вероятности 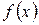 непрерывной случайной величины X:
непрерывной случайной величины X: 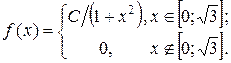 Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) Р(X < 2); 7) построить график
Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) Р(X < 2); 7) построить график 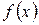 и F(x).
и F(x).
14. задание по мат.статистике см. в конце
Вариант 2
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1. Определить сходимость числового ряда 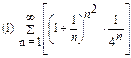
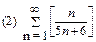
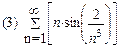
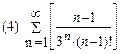
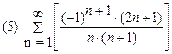
2. Найти область сходимости функционального ряда: 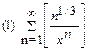
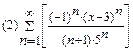
3. Разложить функцию в ряд Маклорена: (1) 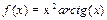 (2)
(2) 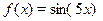 по степеням
по степеням 
Тема «Комплексные числа и теория функции комплексного переменного»
4. Вычислить и записать в алгебраической форме 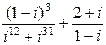 .
.
5. Решить уравнение: 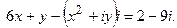
6. Вычислить и записать в тригонометрической форме 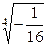
7. Изобразить область, ограниченную линиями: 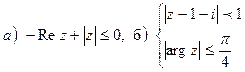
Тема «Операционное исчисление»
8. Используя теоремы линейности, смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a) 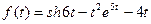 ; б)
; б)  .
.
9. Найти оригинал по заданному изображению:

Тема «Теория вероятностей и математическая статистика».
10. Счетчик регистрирует частицы трех типов: a, b, g. Вероятности появления этих частиц соответственно равны: 0.2, 0.5, 0.3. Частицы каждого из этих типов счетчик улавливает с вероятностями соответственно равными: 0.8, 0.2, 0.4. Найти вероятности событий: 1) А – появившуюся частицу счетчик зарегистрирует; 2) зарегистрированная частица есть частица типа b.
11. Каждый прибор проходит два независимых испытания. Вероятность выхода из строя прибора при первом испытании равна p 1, при втором – p 2 . Испытано независимо n приборов. Найти вероятность выхода из строя не более одного прибора. Вычислить эту вероятность при: 1) n = 5, p 1 = 0.2, p 2 = 0.3 по биномиальной формуле; 2) n =100, p 1 = 0.02, p 2 = 0.03 по формуле Пуассона.
12. СВ 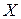 задана законом распределения. Найти: 1) числовые характеристики
задана законом распределения. Найти: 1) числовые характеристики 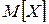 ,
, 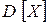 ; 2) функцию распределения
; 2) функцию распределения 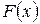 и построить ее график; 3)вероятность
и построить ее график; 3)вероятность 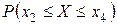 , 4) закон распределения величины СВ
, 4) закон распределения величины СВ 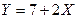 . Вычислить
. Вычислить 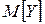 ,
, 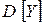 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
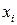
| |||||

| 0, 1 | 0, 2 | 0, 1 | 0, 2 | ? |
13. Дана плотность вероятности f(x) непрерывнойслучайной величины X: 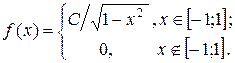 Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6)
Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) 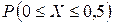 ; 7) построить график f(x) и F(x).
; 7) построить график f(x) и F(x).
14. задание по мат.статистике см. в конце
Вариант 3
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1. Определить сходимость числового ряда 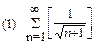
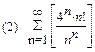
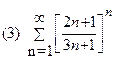
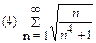
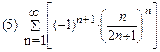
2. Найти область сходимости функционального ряда: 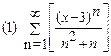
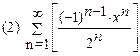
3. Разложить функцию в ряд Маклорена: (1) 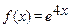 (2)
(2) 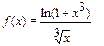 по степеням
по степеням 
Тема «Комплексные числа и теория функции комплексного переменного»
4. Вычислить и записать в алгебраической форме 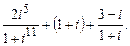 .
.
5. Решить уравнение: 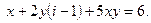
6. Вычислить и записать в тригонометрической форме 
7. Изобразить область, ограниченную линиями: 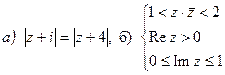
Тема «Операционное исчисление»
8. Используя теоремы линейности, смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a) 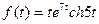 ; б)
; б) 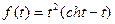 .
.
9. Найти оригинал по заданному изображению:
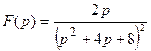
Тема «Теория вероятностей и математическая статистика».
10.Детали партии выпущены двумя заводами, причем детали, выпущенные первым заводом, составляют 40% партии. Вероятность выпуска стандартной детали для первого завода равна 0.9, для второго – 0.95. Найти вероятность того, что случайным образом взятая деталь из партии: 1) окажется стандартной; 2) изготовлена первым заводом, если при проверке она оказалась нестандартной.
11. Устройство содержит n одинаковых деталей 1-го типа и столько же одинаковых деталей 2-го типа. По прошествии времени Т каждая деталь 1-го типа выходит из строя с вероятностью p 1, а каждая деталь 2-го типа – с вероятностью p 2. Найти вероятность того, что через время Т выйдет из строя не более одной детали 1-го типа и ни одной детали 2-го типа. Предполагается, что детали работают независимо друг от друга. Вычислить: 1) эту вероятность с помощью формулы Бернулли при n =100, p 1=0.02, p 2 = 0.01; 2) ту же вероятность с помощью формулы Пуассона.
12. СВ 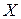 задана законом распределения. Найти: 1) числовые характеристики
задана законом распределения. Найти: 1) числовые характеристики 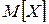 ,
, 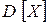 ; 2) функцию распределения
; 2) функцию распределения 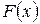 и построить ее график; 3)вероятность
и построить ее график; 3)вероятность 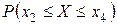 , 4) закон распределения величины СВ
, 4) закон распределения величины СВ 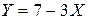 . Вычислить
. Вычислить 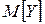 ,
, 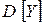 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
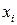
| |||||

| 0, 3 | 0, 1 | 0, 1 | 0, 2 | ? |
13. Дана плотность вероятности f(x) случайной величины X: 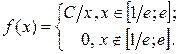 Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) Р(X < 2); 7) построить график f(x) и F(x).
Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) Р(X < 2); 7) построить график f(x) и F(x).
14. задание по мат.статистике см. в конце
Вариант 4
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1. Определить сходимость числового ряда 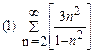
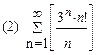
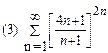
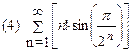
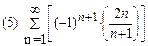
2. Найти область сходимости функционального ряда: 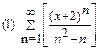
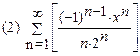
3. Разложить функцию в ряд Маклорена: (1) 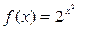 (2)
(2) 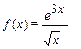 по степеням
по степеням 
Тема «Комплексные числа и теория функции комплексного переменного»
4. Вычислить и записать в алгебраической форме 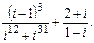 .
.
5. Решить уравнение: 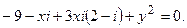
6. Вычислить и записать в тригонометрической форме 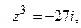
7. Изобразить область, ограниченную линиями: 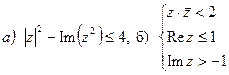
Тема «Операционное исчисление»
8. Используя теоремы линейности, смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a) 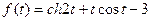 ; б)
; б) 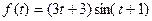 .
.
9. Найти оригинал по заданному изображению:
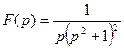 .
.
Тема «Теория вероятностей и математическая статистика».
10. В пункт связи поступают сигналы типов a, b, g соответственно с вероятностями 0.1, 0.4, 0.5. Вследствие помех они могут быть зарегистрированы лишь с вероятностями 0.9, 0.95, 0.92 соответственно. Найти вероятности событий: 1) А – регистрация появившегося сигнала; 2) зарегистрированный сигнал есть сигнал типа a.
11. Вероятность брака детали равна 0.05. После изготовления деталь осматривается контролером, который обнаруживает брак с вероятностью 0.95. Найти вероятность того, что из 100 проверенных деталей забракованных окажется не более одной. Вычислить: 1) эту вероятность с помощью формулы Бернулли, 2) ту же вероятность с помощью формулы Пуассона.
| |||||

| 0, 1 | ? | 0, 1 | 0, 2 | 0, 4 |
12. СВ 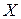 задана законом распределения. Найти: 1) числовые характеристики
задана законом распределения. Найти: 1) числовые характеристики 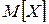 ,
, 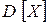 ; 2) функцию распределения
; 2) функцию распределения 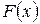 и построить ее график; 3)вероятность
и построить ее график; 3)вероятность 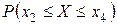 , 4) закон распределения величины СВ
, 4) закон распределения величины СВ 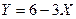 . Вычислить
. Вычислить 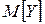 ,
, 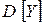 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
13. Дана плотность вероятности f(x) непрерывной случайной величины X: 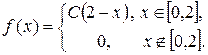 Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6)
Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) 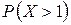 ; 7) построить график f(x) и F(x).
; 7) построить график f(x) и F(x).
14. задание по мат.статистике см. в конце
Вариант 5
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1. Определить сходимость числового ряда 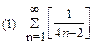
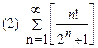
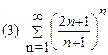
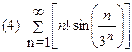
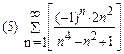
2. Найти область сходимости функционального ряда: 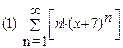
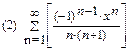
3. Разложить функцию в ряд Маклорена: (1) 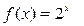 (2)
(2) 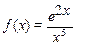 по степеням
по степеням 
Тема «Комплексные числа и теория функции комплексного переменного»
4. Вычислить и записать в алгебраической форме 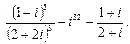 .
.
5. Решить уравнение: 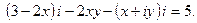
6. Вычислить и записать в тригонометрической форме 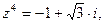
7. Изобразить область, ограниченную линиями: 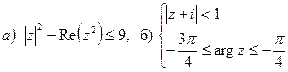
Тема «Операционное исчисление»
8 Используя теоремы линейности, смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a) 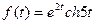 ; б)
; б) 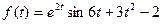 .
.
9 Найти оригинал по заданному изображению:
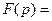
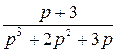 .
.
Тема «Теория вероятностей и математическая статистика».
10. Прибор содержит два независимо работающих блока. Исправность каждого из них необходима для работы прибора. Вероятность отказа блоков за время Т: для первого – p 1=0.1, для второго – p 2 = 0.2. Прибор испытывался в течение времени Т и вышел из строя. Найти: 1) вероятность Р (А) отказа прибора за время Т; 2) вероятность того, что при отказе прибора за время Т отказал только первый блок.
11. По каналу связи посылаются n сообщений. Помехами каждое сообщение может быть искажено с вероятностью p. Найти: 1) каким должно быть n, чтобы хотя бы одно сообщение дошло не искаженным до адресата с вероятностью не меньшей 0.99 при p =0.3; 2) вероятность искажения не более одного сообщения при n =100, p =0.02 (с помощью формулы Пуассона).
12. СВ 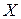 задана законом распределения. Найти: 1) числовые характеристики
задана законом распределения. Найти: 1) числовые характеристики 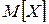 ,
, 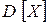 ; 2) функцию распределения
; 2) функцию распределения 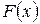 и построить ее график; 3)вероятность
и построить ее график; 3)вероятность 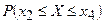 , 4) закон распределения величины СВ
, 4) закон распределения величины СВ 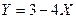 . Вычислить
. Вычислить 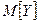 ,
, 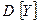 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
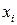
| |||||

| ? | 0, 2 | 0, 1 | 0, 2 | 0, 4 |
13. Дана плотность вероятности f(x) непрерывной случайной величины X: 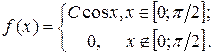 Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) Р(X < 1); 7) построить график f(x) и F(x).
Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) Р(X < 1); 7) построить график f(x) и F(x).
14. задание по мат.статистике см. в конце
Вариант 6
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1. Определить сходимость числового ряда 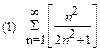
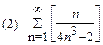
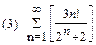
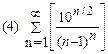
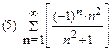
2. Найти область сходимости функционального ряда: 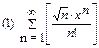
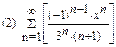
3. Разложить функцию в ряд Маклорена: (1) 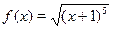 (2)
(2) 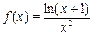 по степеням
по степеням 
Тема «Комплексные числа и теория функции комплексного переменного»
4. Вычислить и записать в алгебраической форме 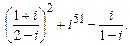 .
.
5. Решить уравнение: 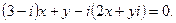
6. Вычислить и записать в тригонометрической форме 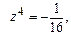
7. Изобразить область, ограниченную линиями: 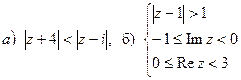
Тема «Операционное исчисление»
8 Используя теоремы линейности, смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a) 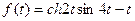 ; б)
; б) 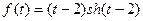 .
.
9 Найти оригинал по заданному изображению:
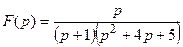 .
.
Тема «Теория вероятностей и математическая статистика».
10. Партия резисторов изготовлена двумя заводами, причем продукции первого завода в 2 раза больше, чем второго. Вероятность брака на первом заводе равна 0.04, на втором – 0.06. Найти вероятность того, что случайным образом взятая деталь партии: 1) оказалась бракованной; 2) изготовлена первым заводом, если при проверке она оказалась бракованной.
11. За период в 131 год с 1865 по 1995 г. в Санкт-Петербурге 10-го января (рождественские морозы) мягкая зимняя погода со среднесуточной температурой от минус 5° до 0° (событие А) наблюдалась 35 раз, а не ниже минус +2° (событие В) – всего 5 раз. Исходя из этих статистических данных, примем Р(А)=35/131=0.27, Р(В)=5/131=0.04. Найти вероятность: 1) того, что в предстоящие ближайшие 4 года событие А будет наблюдаться не менее двух раз; 2) появления события В хотя бы один раз в предстоящие 20 последовательных лет с помощью формулы Пуассона.
12. СВ 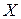 задана законом распределения. Найти: 1) числовые характеристики
задана законом распределения. Найти: 1) числовые характеристики 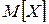 ,
, 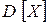 ; 2) функцию распределения
; 2) функцию распределения 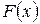 и построить ее график; 3)вероятность
и построить ее график; 3)вероятность 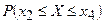 , 4) закон распределения величины СВ
, 4) закон распределения величины СВ 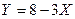 . Вычислить
. Вычислить 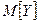 ,
, 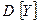 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
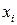
| |||||

| 0, 1 | ? | 0, 1 | 0, 2 | 0, 4 |
13. Дана плотность вероятности f(x) НСВ X: 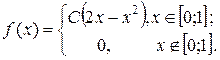 Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6)
Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) 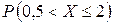 ; 7) построить график f(x) и F(x).
; 7) построить график f(x) и F(x).
14. задание по мат.статистике см. в конце
Вариант 7
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1. Определить сходимость числового ряда 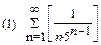
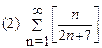
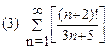
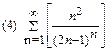
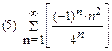
2. Найти область сходимости функционального ряда: 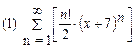
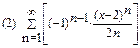
3. Разложить функцию в ряд Маклорена: (1) 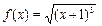 (2)
(2) 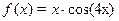 по степеням
по степеням 
Тема «Комплексные числа и теория функции комплексного переменного»
4. Вычислить и записать в алгебраической форме 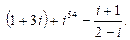 .
.
5. Решить уравнение: 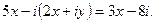
6. Вычислить и записать в тригонометрической форме 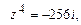
7. Изобразить область, ограниченную линиями: 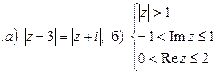
Тема «Операционное исчисление»
8 Используя теоремы линейности, смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a) 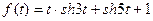 ; б)
; б) 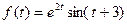 .
.
9 Найти оригинал по заданному изображению:
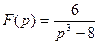 .
.
Тема «Теория вероятностей и математическая статистика».
10. Партия резисторов изготовлена двумя заводами, причем продукции первого завода в 2 раза больше, чем второго. Вероятность брака на первом заводе равна 0.04, на втором – 0.06. Найти вероятность того, что случайным образом взятая деталь партии: 1) оказалась бракованной; 2) изготовлена первым заводом, если при проверке она оказалась бракованной.
11. За период в 131 год с 1865 по 1995 г. в Санкт-Петербурге 10-го января (рождественские морозы) мягкая зимняя погода со среднесуточной температурой от минус 5° до 0° (событие А) наблюдалась 35 раз, а не ниже минус +2° (событие В) – всего 5 раз. Исходя из этих статистических данных, примем Р(А)=35/131=0.27, Р(В)=5/131=0.04. Найти вероятность: 1) того, что в предстоящие ближайшие 4 года событие А будет наблюдаться не менее двух раз; 2) появления события В хотя бы один раз в предстоящие 20 последовательных лет с помощью формулы Пуассона.
12. СВ 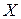 задана законом распределения. Найти: 1) числовые характеристики
задана законом распределения. Найти: 1) числовые характеристики 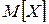 ,
, 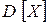 ; 2) функцию распределения
; 2) функцию распределения 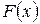 и построить ее график; 3)вероятность
и построить ее график; 3)вероятность 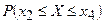 , 4) закон распределения величины СВ
, 4) закон распределения величины СВ 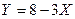 . Вычислить
. Вычислить 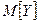 ,
, 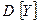 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
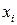
| |||||

| 0, 1 | ? | 0, 1 | 0, 2 | 0, 4 |
13. Дана плотность вероятности f(x) НСВ X: 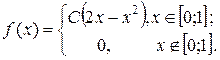 Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6)
Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) 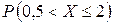 ; 7) построить график f(x) и F(x).
; 7) построить график f(x) и F(x).
14. задание по мат.статистике см. в конце
Вариант 8
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1. Определить сходимость числового ряда 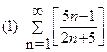
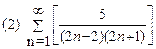
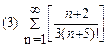
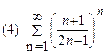
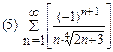
2. Найти область сходимости функционального ряда: 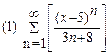
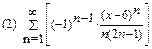
3. Разложить функцию в ряд Маклорена: (1) 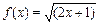 (2)
(2) 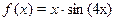 по степеням
по степеням 
Тема «Комплексные числа и теория функции комплексного переменного»
4. Вычислить и записать в алгебраической форме 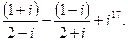 .
.
5. Решить уравнение: 
6. Вычислить и записать в тригонометрической форме 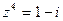
7. Изобразить область, ограниченную линиями: 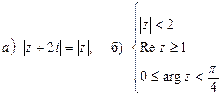
Тема «Операционное исчисление»
8 Используя теоремы линейности, смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a) 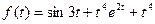 ; б)
; б) 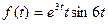 .
.
9 Найти оригинал по заданному изображению:
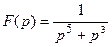 .
.
Тема «Теория вероятностей и математическая статистика».
10. Сообщение состоит из сигналов «1» и «0». Свойства помех таковы, что искажаются в среднем 5% сигналов «0» и 3% сигналов «1». При искажении вместо сигнала «0» принимается сигнал «1» и наоборот. Известно, что среди передаваемых сигналов «0» и «1» встречаются в соотношении 3: 2. Найти вероятность того, что: 1) отправленный сигнал будет принят как «1»; 2) отправлен сигнал «0», если принят сигнал «1».
11. В партии п =100 деталей. Вероятность брака детали равна р = 0.02. Найти: 1) с помощью формулы Бернулли вероятность того, что в партии не более двух бракованных деталей; 2) ту же вероятность с помощью формулы Пуассона.
12. СВ 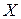 задана законом распределения. Найти: 1) числовые характеристики
задана законом распределения. Найти: 1) числовые характеристики 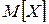 ,
, 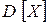 ; 2) функцию распределения
; 2) функцию распределения 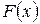 и построить ее график; 3)вероятность
и построить ее график; 3)вероятность 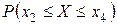 , 4) закон распределения величины СВ
, 4) закон распределения величины СВ 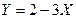 . Вычислить
. Вычислить 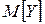 ,
, 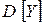 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
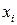
| |||||

| 0, 4 | 0, 2 | ? | 0, 2 | 0, 1 |
13. Дана плотность вероятности f(x) случайной величины X: 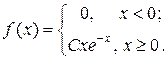 Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) Р(X < 3); 7) построить график f(x) и F(x).
Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) Р(X < 3); 7) построить график f(x) и F(x).
14. задание по мат.статистике см. в конце
Вариант 9
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1. Определить сходимость числового ряда 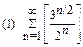
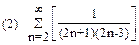
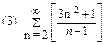
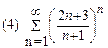
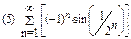
2. Найти область сходимости функционального ряда: 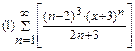
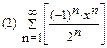
3. Разложить функцию в ряд Маклорена: (1) 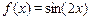 (2)
(2) 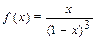 по степеням
по степеням 
Тема «Комплексные числа и теория функции комплексного переменного»
4. Вычислить и записать в алгебраической форме 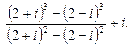 .
.
5. Решить уравнение: 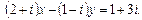
6. Вычислить и записать в тригонометрической форме 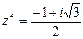
7. Изобразить область, ограниченную линиями: 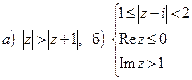
Тема «Операционное исчисление»
8 Используя теоремы линейности, смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a)  ; б)
; б) 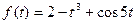 .
.
9 Найти оригинал по заданному изображению:
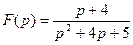 .
.
Тема «Теория вероятностей и математическая статистика».
10. Произведено два выстрела по цели. Вероятность попадания при каждом выстреле равна 0.7. Цель поражается с одного попадания с вероятностью 0.5, при двух попаданиях – с вероятностью 0.9. Найти вероятность: 1) поражения цели при двух выстрелах; 2) того, что оба снаряда попали в цель, если окажется, что цель поражена.
11. На каждом станке за смену выпускается п деталей. Вероятность брака для первого станка равна р 1, для второго – р 2. Найти вероятность р того, что в сменной продукции обоих станков не более одной бракованной детали. Вычислить эту вероятность при: 1) n = 8, p 1 = 0.05, p 2 = 0.03; 2) n =100, p 1 = 0.005, p 2 = 0.003 по формуле Пуассона.
12. СВ 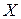 задана законом распределения. Найти: 1) числовые характеристики
задана законом распределения. Найти: 1) числовые характеристики 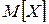 ,
, 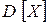 ; 2) функцию распределения
; 2) функцию распределения 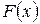 и построить ее график; 3)вероятность
и построить ее график; 3)вероятность 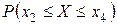 , 4) закон распределения величины СВ
, 4) закон распределения величины СВ 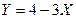 . Вычислить
. Вычислить 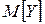 ,
, 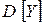 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
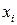
| |||||

| 0, 2 | 0, 1 | 0, 2 | 0, 4 | ? |
13. Дана плотность вероятности f(x) случайной величины X: 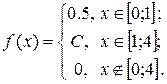 Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) Р(X < 2); 7) построить график f(x) и F(x).
Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) Р(X < 2); 7) построить график f(x) и F(x).
14. задание по мат.статистике см. в конце
Вариант 0
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1. Определить сходимость числового ряда 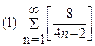
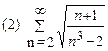
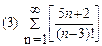
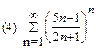
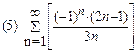
2. Найти область сходимости функционального ряда: 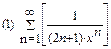
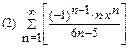
3. Разложить функцию в ряд Маклорена: (1) 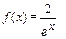 (2)
(2) 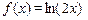 по степеням
по степеням 
Тема «Комплексные числа и теория функции комплексного переменного»
4. Вычислить и записать в алгебраической форме 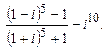 .
.
5. Решить уравнение: 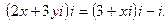
6. Вычислить и записать в тригонометрической форме 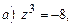
7. Изобразить область, ограниченную линиями: 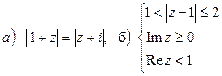
Тема «Операционное исчисление»
8 Используя теоремы линейности, смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a) 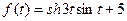 ; б)
; б) 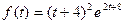 .
.
9 Найти оригинал по заданному изображению:
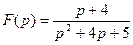 .
.
Тема «Теория вероятностей и математическая статистика».
10. На любой из позиций импульсного кода могут быть с равной вероятностью переданы «0» (отсутствие импульса) и «1» (импульс). Помехами «1» преобразуется в «0» с вероятностью 0.02 и «0» в «1» с вероятностью 0.04. Найти вероятность: 1) приема «0» на конкретной позиции кода; 2) того, что был передан «0», если принят «0».
11. В первой партии – 100 деталей. Вероятность брака в этой партии – 0.01. Во второй партии – 200 деталей, вероятность брака – 0.005. Найти вероятность того, что в обеих партиях нет бракованных деталей. Вычислить: 1) эту вероятность по формуле Бернулли; 2) ту же вероятность с помощью формулы Пуассона.
12. СВ 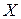 задана законом распределения. Найти: 1) числовые характеристики
задана законом распределения. Найти: 1) числовые характеристики 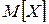 ,
, 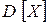 ; 2) функцию распределения
; 2) функцию распределения 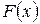 и построить ее график; 3)вероятность
и построить ее график; 3)вероятность 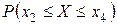 , 4) закон распределения величины СВ
, 4) закон распределения величины СВ 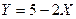 . Вычислить
. Вычислить 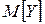 ,
, 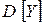 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
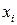
| |||||

| ? | 0, 1 | 0, 2 | 0, 4 | 0, 1 |
13. Дана плотность вероятности f(x) НСВ X: 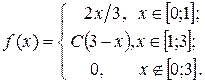 Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6)
Найти: 1) С; 2) F(x); 3) mX; 4) DX; 5) s(x); 6) 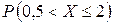 ; 7) построить график f(x) и F(x).
; 7) построить график f(x) и F(x).
14. задание по мат.статистике см. в конце
Задание по матем. статистике
1. Результаты измерений представлены таблицей. Составить вариационный ряд, разбив всю вариацию на 9–10 интервалов.
2. Построить: а) полигон частот;
б) гистограмму частот;
в) график эмпирической функции распределения.
3. Выдвинуть гипотезу о распределении генеральной совокупности.
4. Найти числовые характеристики выборки: 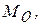
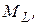
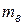 ,
, 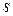 ,
, 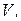
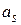 ,
, 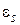 .
.
5. Найти доверительные интервалы для генеральной средней и генерального среднего квадратического отклонения по следующим уровням надежности:
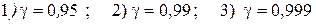 .
.
6. Построить кривую распределения 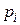 по опытным данным. Сравнить её с графиком идеально нормального распределения, используя
по опытным данным. Сравнить её с графиком идеально нормального распределения, используя 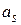 ,
, 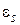 .
.
7. Проверить правило ''3-x 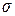 ''.
''.
8. Применив критерий согласия Пирсона–χ 2 с заданным уравнением надежности = 0, 05, окончательно принять или отвергнуть выдвинутую гипотезу о распределении генеральной совокупности.
| вариант №1 | ||||||||||
| вариант №2 | ||||||||||
| вариант №3 | ||||||||||
| вариант №4 | ||||||||||
| вариант №5 | ||||||||||
| вариант №6 | ||||||||||
| вариант №7 | ||||||||||