Приложения частных производных

2.1. Составить уравнение касательной плоскости и уравнение нормали к поверхности 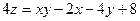в точке .

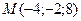Решение. Проверим, принадлежит ли точка М поверхности:

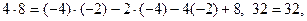
следовательно, точка М принадлежит поверхности.

Уравнение касательной плоскости имеет вид:

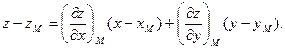
Найдем значения частных производных в точке М:

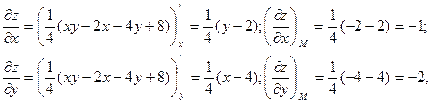
и подставим в уравнение касательной плоскости:

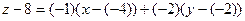или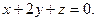

Уравнение нормали берем в виде:

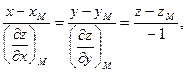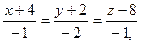или или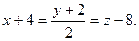

2.2. Найти градиент и производную по направлению 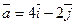функции 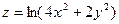в точке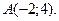

Решение. Градиент функции 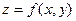равен:

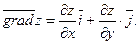
Найдем частные производные:

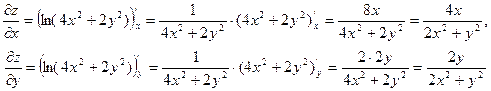
и их значения в точке :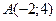

.

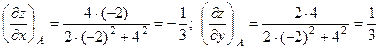Тогда градиент в точке А равен:

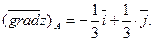
Производная функции z в направлении вектора 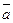вычисляется по формуле:

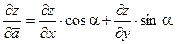
Найдем направляющие косинусы вектора :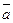

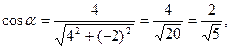
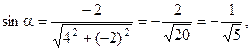
Следовательно,

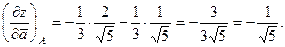
2.3. Найти наибольшее и наименьшее значение функции

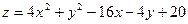
в замкнутой области D, заданной неравенствами:

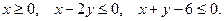
Решение.

а) Найдем частные производные и приравняем их к нулю (необходимые условия экстремума):

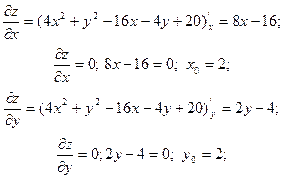
Стационарная точка 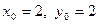лежит в замкнутой области, так как:

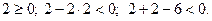
Найдем вторые частные производные:

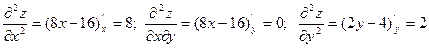
и их значения в стационарной точке М (2; 2):

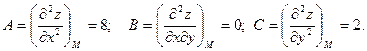
Так как 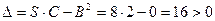, то в точке М функция имеет экстремум, а именно минимум, так как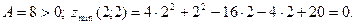

б) Построим замкнутую область ОАВ (рис. 1)

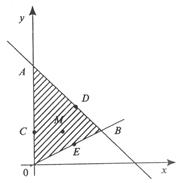
Рис.1

Рассмотрим контур 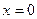(прямая ОА). Имеем функцию одной переменной: 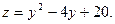Исследуем ее на экстремум:

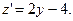
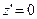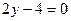Из имеем или 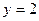. И так как

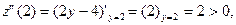
то имеем минимум и

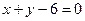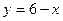Далее рассмотрим контур или (прямая АВ). Имеем:

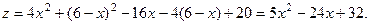
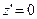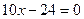Найдем и из имеем или .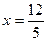

Так как 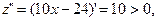то при 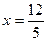имеем минимум и

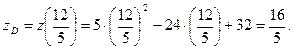
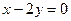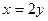На контуре или (прямая ОВ) имеем 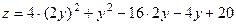или 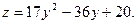Находим производную 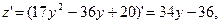приравниваем ее к нулю 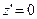или 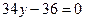, отсюда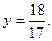

Так как 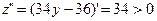, то в точке 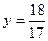имеем минимум и

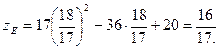
Найдем значение функции z в точках О (0; 0), А (0; 6) и В (4; 2):

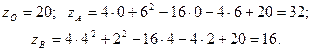
Из найденных значений 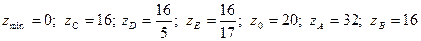выбираем наименьшее и наибольшее. Получаем, что