
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Геометрический метод решения ЗЛП
|
|
Геометрический метод решения ЗЛП применяется в случае, если задача содержит не более двух переменных или может быть сведена к таковой.
Каждое из неравенств системы ограничений геометрически определяет полуплоскость допустимых значений переменных с граничными прямыми.
Алгоритм геометрического метода:
1. В системе ограничений знаки неравенств заменяются на знаки точных равенств и по полученным уравнениям строятся прямые на плоскости x 1 Ox 2.
2. Определяются полуплоскости – области решения неравенств, и строится многоугольник решений (ОДР), который получается в результате пересечения полуплоскостей. Стороны этого многоугольника являются прямыми уравнений системы ограничений.
4. Из точки (0; 0) строится вектор  , направление которого определяет направление возрастания целевой функции
, направление которого определяет направление возрастания целевой функции 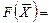 c 1 x 1 + c 2 x 2.
c 1 x 1 + c 2 x 2.
5. Строится начальная прямая (линия нулевого уровня) целевой функции 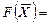 c 1 x 1 + c 2 x 2 = 0, которую передвигают в направлении вектора
c 1 x 1 + c 2 x 2 = 0, которую передвигают в направлении вектора 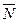 до крайней угловой точки многоугольника решений. В этой точке целевая функция принимает max значение.
до крайней угловой точки многоугольника решений. В этой точке целевая функция принимает max значение.
6. Определяются координаты точки максимума целевой функции 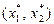 как точки пересечения соответствующих прямых и вычисляется значение целевой функции в этой точке
как точки пересечения соответствующих прямых и вычисляется значение целевой функции в этой точке 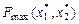 .
.
В нашем случае система уравнений будет иметь вид:
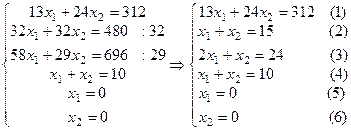
Построим по полученным уравнениям прямые и пронумеруем их (рис.1). Областью ОДР будет выпуклый многоугольник АBCDEF, каждая вершина которого является опорным планом. Из точки (0; 0) строим вектор 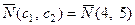 . Начальная линия уровня будет иметь вид:
. Начальная линия уровня будет иметь вид: 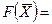 4 x 1 + 3 x 2 = 0. Перемещая линию уровня вдоль вектора
4 x 1 + 3 x 2 = 0. Перемещая линию уровня вдоль вектора 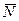 , получим, что функция F принимает max значение в точке D – самой крайней справа вершине многоугольника ОДР. Точка D является точкой пересечения прямых (2) и (3). Находим координаты точки D, решая систему уравнений этих прямых:
, получим, что функция F принимает max значение в точке D – самой крайней справа вершине многоугольника ОДР. Точка D является точкой пересечения прямых (2) и (3). Находим координаты точки D, решая систему уравнений этих прямых:
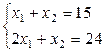 .
.
Решением системы будут значения x 1 = 9, x 2 = 6, т.е. D (9; 6). Тогда 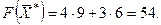
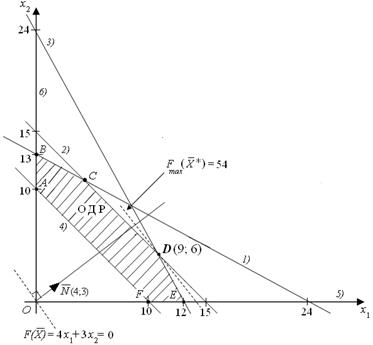
Рис. 1. Иллюстрация геометрического метода решения ЗЛП
Таким образом, решением задачи будет оптимальный план 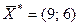 , дающий max значение функции
, дающий max значение функции 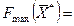 54 у.е. Максимальная прибыль 54 у.е. достигается при изготовлении 9 единиц изделий I вида и 6 единиц изделий II вида.
54 у.е. Максимальная прибыль 54 у.е. достигается при изготовлении 9 единиц изделий I вида и 6 единиц изделий II вида.
В данной задаче ОДР является выпуклый многоугольник. Однако возможны и следующие случаи:
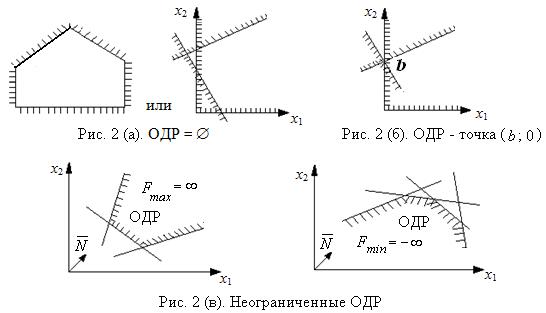
1) ОДР – пустое множество (рис.2, а). В этом случае задача линейного программирования не имеет решения из-за несовместности системы ограничений.
2) ОДР – единственная точка, которая и будет единственным и оптимальным решением (рис.2, б).
3) ОДР – выпуклая неограниченная область (рис.2, в). В задаче на max оптимальное решение не существует, если целевая функция не ограничена сверху (Fmax = ∞). В задаче на min оптимальное решение не существует, если целевая функция не ограничена снизу (Fmin = –∞).
4) Может оказаться, что линия уровня функции F совпадает с одной из сторон многоугольника ОДР (экстремум целевой функции достигается на всем отрезке между двумя соседними вершинами ОДР) (рис.3). Тогда имеет место альтернативный оптимум: 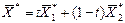 , где t є [0; 1] – параметр.
, где t є [0; 1] – параметр.
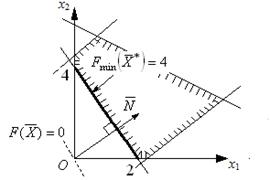
Рис. 3. Альтернативный оптимум
Формы записи задачи линейного программирования
Существуют три формы записи ЗЛП: каноническая, стандартная, общая.
В канонической (основной) форме все ограничения имеют вид уравнений, т.е. 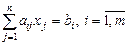 , а также условие неотрицательности накладывается на все переменные:
, а также условие неотрицательности накладывается на все переменные: 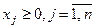 . В стандартной форме все ограничения записаны в виде нестрогих неравенств, и также
. В стандартной форме все ограничения записаны в виде нестрогих неравенств, и также 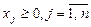 . В общей формеограничения могут быть представлены как уравнениями, так и неравенствами, а условие неотрицательности может накладываться не на все, а только на часть переменных
. В общей формеограничения могут быть представлены как уравнениями, так и неравенствами, а условие неотрицательности может накладываться не на все, а только на часть переменных 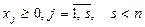 .
.