
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методика выполнения работы. Задача определения напряжения на выходе линейной цепи может решаться различными методами [1]:
|
|
4.1. Выбор метода расчета
Задача определения напряжения на выходе линейной цепи может решаться различными методами [1]:
- классическим, с помощью составления и решения дифференциальных уравнений электрического равновесия цепи при заданном входном воздействии;
- спектральным, путем определения комплексного коэффициента передачи цепи и спектра входного сигнала с последующим вычислением спектра выходного напряжения и затем его временной реализации;
- операторным, на базе операторного коэффициента передачи цепи и изображения по Лапласу входного воздействия с последующим вычислением изображения выходного напряжения и его оригинала (выходного сигнала);
- временным (интеграла Дюамеля).
Для расчета выходного напряжения удобно использовать метод интеграла Дюамеля, который не требует операций с комплексными числами.
Выходное напряжение 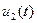 определяется одним из выражений
определяется одним из выражений
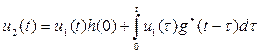 , (1)
, (1)
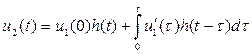 , (2)
, (2)
где 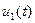 - входное напряжение,
- входное напряжение, 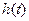 - переходная характеристика цепи,
- переходная характеристика цепи, 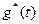 - импульсная характеристика без
- импульсная характеристика без  -функций, «штрих» в обозначении функции указывает на дифференцирование по аргументу. Предполагается, что переходная характеристика цепи и входной сигнал могут иметь разрыв первого рода только в точке
-функций, «штрих» в обозначении функции указывает на дифференцирование по аргументу. Предполагается, что переходная характеристика цепи и входной сигнал могут иметь разрыв первого рода только в точке 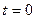 . В большинстве случаев целесообразнее использовать первую формулу, так как в ней не требуется дифференцировать входной сигнал.
. В большинстве случаев целесообразнее использовать первую формулу, так как в ней не требуется дифференцировать входной сигнал.
4.2. Определение переходной и импульсной характеристик
Переходную и импульсную характеристики цепи можно определить операторным или классическим методами.
В курсовой работе рекомендуется операторный метод, базирующийся на преобразовании Лапласа. Прежде всего необходимо найти операторный коэффициент передачи цепи 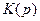 , тогда
, тогда
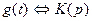 , (3)
, (3)
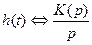 , (4)
, (4)
где символ 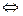 обозначает соответствие оригинала и изображения по Лапласу. Обычно преобразование Лапласа находится по таблицам, приведенным в учебниках по курсу «Основы теории цепей», например, в [1], или в справочниках [2-5].
обозначает соответствие оригинала и изображения по Лапласу. Обычно преобразование Лапласа находится по таблицам, приведенным в учебниках по курсу «Основы теории цепей», например, в [1], или в справочниках [2-5].
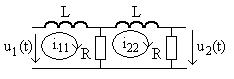
В качестве примера рассмотрим цепь на рис. 1, в которой обозначены входное и выходное напряжения и контурные токи. Тогда запишем систему уравнений цепи по методу контур-
Рис. 1. ных токов,
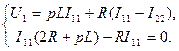 (5)
(5)
Решив систему (5), с учетом 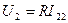 , получим
, получим
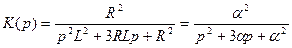 , (6)
, (6)
где
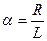 . (7)
. (7)
Решая квадратное уравнение
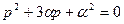 , (8)
, (8)
получим его корни
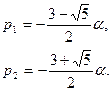 (9)
(9)
В результате для операторного коэффициента передачи получим
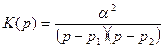 . (10)
. (10)
По таблицам преобразования Лапласа [1] определим
 , (11)
, (11)
тогда для импульсной характеристики цепи 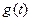 получим
получим
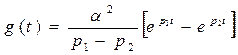 , (12)
, (12)
а с учетом (9)
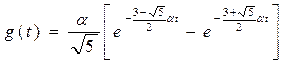 . (13)
. (13)
Переходная характеристика 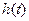 является оригиналом от
является оригиналом от
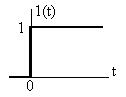
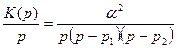 , (14)
, (14)
а согласно [1]
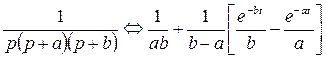 . (15)
. (15)
Тогда, подставляя (9), получим
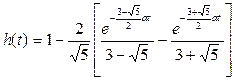 . (16)
. (16)
На рис. 2 показаны переходная (16) и импульсная (13) характеристики при 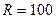 Ом и
Ом и 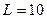 мГн.
мГн.
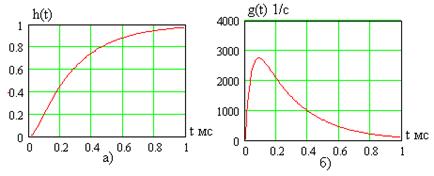
Рис.2
Для проверки расчетов временных характеристик можно воспользоваться соотношением
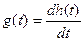 . (17)
. (17)
Переходная характеристика численно равна реакции цепи на единичную функцию (функцию Хевисайда) вида рис. 3. В момент скачка t=0 ток в индуктивности остается равным нулю, а значит выходное напряжение, снимаемое с сопро-
Рис. 3 тивления, будет равно нулю. По истечении
значительного времени после коммутации токи и напряжения в цепи будут постоянными. При этом индуктивность представляет собой короткое замыкание, выходное напряжение будет равно входному, а переходная характеристика – единице.
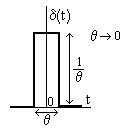 Импульсная характеристика численно равна реакции цепи на входное воздействие в виде единичного импульса (функции Дирака), показанного на рис. 4. Это импульс с нулевой длительностью и бесконечной амплитудой. Он мгновенно заряжает энергией (током) первую индуктивность, и затем под его воздействием начинает возрастать ток второй индуктивности, а на выходе появляется напряжение. Затем поступившая в цепь энергия рассеивается и выходное напряжение падает. Подобный анализ необходимо проводить и в курсовой работе.
Импульсная характеристика численно равна реакции цепи на входное воздействие в виде единичного импульса (функции Дирака), показанного на рис. 4. Это импульс с нулевой длительностью и бесконечной амплитудой. Он мгновенно заряжает энергией (током) первую индуктивность, и затем под его воздействием начинает возрастать ток второй индуктивности, а на выходе появляется напряжение. Затем поступившая в цепь энергия рассеивается и выходное напряжение падает. Подобный анализ необходимо проводить и в курсовой работе.
Рис. 4
4.3. Аналитический расчет выходного напряжения
В каждом варианте задания входное воздействие представлено в виде двух функций:
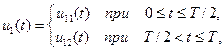 (18)
(18)
из которых одна является простой, допускающей аналитическое интегрирование, а другая – сложной.
Если простой является первая часть входного воздействия 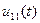 , то выходное напряжение
, то выходное напряжение 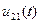 легко вычисляется, например, по формуле (1) в виде
легко вычисляется, например, по формуле (1) в виде
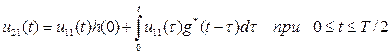 . (19)
. (19)
Если же простой оказывается вторая часть 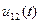 входного сигнала на интервале времени от
входного сигнала на интервале времени от 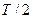 до
до 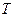 , то выходное напряжение определяется, например, выражением
, то выходное напряжение определяется, например, выражением
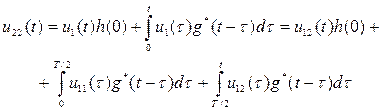 (20)
(20)
при  .
.
Второй интеграл в правой части (20) вида
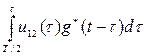 (21)
(21)
от простой подынтегральной функции вычисляется обычными методами. Первый интеграл вида
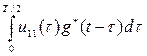 (22)
(22)
от сложной подынтегральной функции переменной 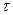 , но в фиксированных пределах, также вычисляется аналитически, то есть выражается в элементарных функциях (экспонентах) переменной
, но в фиксированных пределах, также вычисляется аналитически, то есть выражается в элементарных функциях (экспонентах) переменной 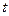 . Импульсную характеристику апериодической цепи можно представить в виде суммы
. Импульсную характеристику апериодической цепи можно представить в виде суммы
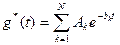 , (23)
, (23)
где 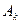 и
и 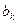 - действительные коэффициенты, а
- действительные коэффициенты, а 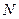 - число слагаемых.
- число слагаемых.
Подставляя (23) в (22) и заменяя 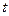 на
на 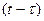 , с учетом того, что переменная
, с учетом того, что переменная 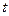 является константой при интегрировании по
является константой при интегрировании по 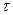 , получим
, получим
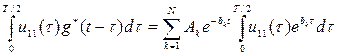 . (24)
. (24)
Интегралы вида
 (25)
(25)
от сложной подынтегральной функции в фиксированных пределах представляют собой константы (действительные числа), которые должны находиться численными методами, например, с помощью пакета программ MathCAD. С точки зрения качества подготовки целесообразней разработать самостоятельную программу на любом языке высокого уровня.
Складывая полученные выражения в соответствии с (20) или используя (19), необходимо записать общее аналитическое выражение (формулу) для выходного сигнала, вычислить таблицу значений и построить график на соответствующем интервале времени. Кроме того, следует провести физический анализ влияния цепи на выходной сигнал.
4.4. Численный расчет выходного напряжения
Численный расчет выходного сигнала на всем интервале времени от 0 до T проводится так, как будто все интегралы являются не берущимися (на рекомендуется даже выносить за знак интегралов постоянные множители). Для вычисления выходного сигнала необходимо разработать программу на любом языке высокого уровня. Она базируется на процедуре численного интегрирования на основе известных алгоритмов, например, по формулам прямоугольников, трапеций, парабол (Симпсона) и другим [4-6].
В общем случае вычисляется интеграл
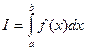 . (26)
. (26)
Интервал интегрирования разбивается на 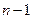 отрезков с шагом
отрезков с шагом 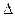 ,
,
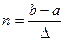 , (27)
, (27)
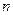 - целое число. Обозначим
- целое число. Обозначим
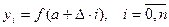 , (28)
, (28)
тогда по формуле прямоугольников
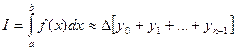 ; (29)
; (29)
по формуле трапеций
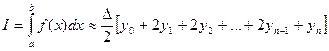 ; (30)
; (30)
по формуле парабол (Симпсона)
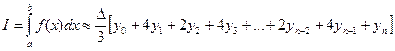 . (31)
. (31)
Численное интегрирование проводится с ошибкой, которую для метода Симпсона приближенно можно оценить величиной
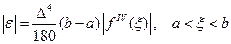 , (32)
, (32)
где 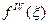 - четвертая производная интегрируемой функции в некоторой точке на интервале интегрирования. Метод Симпсона обеспечивает минимальную погрешность интегрирования при заданном числе интервалов
- четвертая производная интегрируемой функции в некоторой точке на интервале интегрирования. Метод Симпсона обеспечивает минимальную погрешность интегрирования при заданном числе интервалов 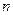 , которое обычно выбирается от 30 до 50.
, которое обычно выбирается от 30 до 50.
В курсовой работе погрешность вычисления выходного сигнала различными методами численного интегрирования можно оценить сравнением полученных значений с результатами аналитического расчета. Целесообразно провести сравнительный анализ эффективности различных методов численного интегрирования.
4.5. Табуляция функций времени
Входное воздействие, переходную и импульсную характеристики, аналитические и численные результаты расчета выходного сигнала необходимо представить в виде таблиц и графиков.
Табулирование всех временных зависимостей должно проводиться на интервале от 0 до 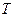 (при необходимости и далее) с числом точек не менее 20-40 в зависимости от характера функции. Для построения графиков достаточно выводить данные с тремя значащими цифрами, а для сравнения результатов численного и аналитического расчета и оценки погрешности необходимо использовать максимальное (до 15) число значащих цифр.
(при необходимости и далее) с числом точек не менее 20-40 в зависимости от характера функции. Для построения графиков достаточно выводить данные с тремя значащими цифрами, а для сравнения результатов численного и аналитического расчета и оценки погрешности необходимо использовать максимальное (до 15) число значащих цифр.
4.6. Программа вычислений
Программа вычислений в рамках курсовой работы может решать, например, следующие задачи:
- численного расчета и табуляции выходного сигнала на интервале времени от 0 до 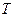 (минимальный вариант);
(минимальный вариант);
- расчета, табуляции и построения графиков входного и выходного сигналов, результатов аналитического расчета и временных характеристик цепи;
- расчета характеристик цепи с элементами САПР;
- оптимизации характеристик цепи (например коэффициента прямоугольности) при изменении параметров элементов;
- расчета влияния температуры и других внешних факторов на свойства цепи и выходной сигнал;
- статистического моделирования влияния разброса параметров элементов цепи на ее свойства;
- проведения экспериментальных исследований цепи с вводом-выводом сигналов с помощью звуковой карты компьютера.
Программа может быть написана на любом языке высокого уровня [6] (кроме MathCAD), целесообразно использовать системы объектно-ориентированного программирования (С, Delphi), создавать развитый графический интерфейс.
4.7. Экспериментальные исследования
Результаты расчетов проверяются экспериментально в лаборатории с помощью установки, структурная схема которой показана на рис. 5.
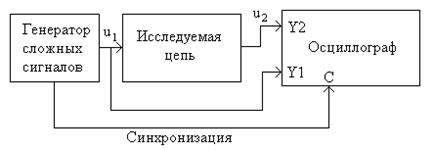
Рис. 5
Студент дома самостоятельно монтирует исследуемую цепь на макетной плате или собирает ее в лаборатории на плате лабораторного стенда. К цепи подключается генератор сложных сигналов и переключателем выбирается требуемый вариант воздействия. Входной и выходной сигналы цепи подаются в каналы вертикального отклонения Y1 и Y2 электронного осциллографа С1-55, на вход внешней синхронизации С подается соответствующий сигнал генератора [7].
Регулировкой уровня и длительности сигнала генератора добиваемся наилучшего совпадения входного сигнала цепи заданному в варианте задания воздействию. Записываем в таблицу 10-20 значений, измеренных по экрану осциллографа, строим совместный график расчетного и экспериментального входного напряжения, оцениваем погрешность.
Установив требуемое входное воздействие, измеряем по экрану осциллографа выходное напряжение (10-20 значений), заносим результаты в таблицу, сравниваем с расчетными величинами, строим совместный график расчетного и экспериментального выходного напряжения, оцениваем погрешность.
В качестве дополнительного задания целесообразно измерить:
- частотные характеристики цепи;
- переходную и импульсную характеристики цепи, разработав необходимые методики, а затем сравнить результаты расчетов и измерений.
4.8. Схемотехническое моделирование
Схемотехническое моделирование с помощью пакетов программ WorkBench, MicroCAP или OrCAD позволяет проводить многообразные исследования свойств электрических сигналов и цепей [9-10].
Методами моделирования можно определить частотные и временные характеристики цепи, с помощью файла отсчетов сформировать сложный входной сигнал и определить выходное напряжение цепи. Результаты моделирования необходимо сравнить с аналогичными материалами, полученными в результате расчетов и экспериментальных исследований. Если графики отображаются в различных масштабах (линейном, логарифмическом), то сравнительный анализ удобно проводить по сводным таблицам, полученным при одинаковых значениях переменной.
В качестве дополнительного или исследовательского задания можно провести моделирование различных электронных устройств (усилителей, генераторов), в том числе и с подключением их к заданной цепи.