Условия сходимости метода Зейделя

Разложим матрицу на сумму 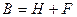, где

, ,

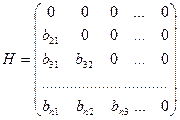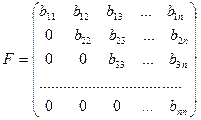тогда (7) можно записать в матричном виде:

,

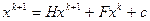или

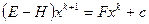. (8)

Поскольку

,

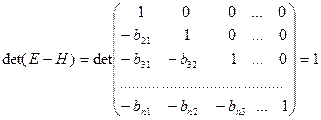то существует , 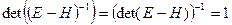. Умножим равенство (8) на слева:

.

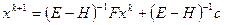Таким образом, стационарный метод Зейделя эквивалентен МПИ для решения системы

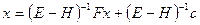. (9)

А это значит, что метод Зейделя будет сходиться, когда будет сходиться МПИ для системы (9), т.е. тогда, когда модули СЗ матрицы 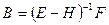будут меньше 1, или, что тоже самое, когда все корни характеристического уравнения

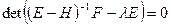(10)

по модулю будут меньше 1.

Перепишем уравнение (10) в виде:

.

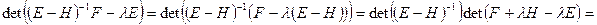
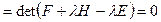Тогда очевидно имеет место следующая теорема.

Теорема 3. Для того, чтобы стационарный метод Зейделя сходился при любом начальном приближении 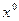, необходимо и достаточно, чтобы все корни уравнения 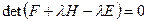по модулю были меньше 1.

Замечание 3 (вычислительная сложность стационарного метода Зейделя). Основная расчетная формула стационарного метода Зейделя – это формула (7), которая определяет действия данного алгоритма на каждой итерации. Аналогично замечанию 2, можно утверждать, что в итоге, каждая итерация метода Зейделя требует 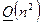операций, тогда в целом количество арифметических операций, необходимых для решения СЛАУ методом Зейделя, определиться как

,

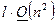где 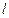- это количество итераций, затраченных в методе Зейделя для достижения заданной точности решения .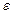