Метод градиентного спуска. Рассмотрим СЛАУ (1). Пусть матрица является симметричной и положительно определенной

Рассмотрим СЛАУ (1). Пусть матрица 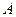является симметричной и положительно определенной. Поставим в соответствие СЛАУ (1) многочлен:

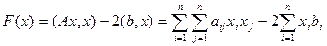, (11)

который называется функционалом энергии.

Утверждение 1. Если матрица 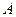является симметричной и положительно определенной, то многочлен (11) имеет единственный минимум.

Существует определенная связь между двумя задачами: задачей решения СЛАУ (1) и задачей минимизации функционала (11).

Теорема 4. Если в некоторой точке 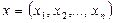n -мерного векторного пространства многочлен (11) имеет минимум, то координаты этой точки 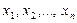являются решением СЛАУ (1).

Теорема 5. Если 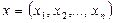- решение СЛАУ (1), то многочлен (11) принимает в этой точке свой абсолютный минимум по всему n -мерному пространству.

Из теорем 4, 5 вытекает, что задача решения СЛАУ (1) для симметричной и положительно определенной матрицы эквивалентна задаче минимизации функционала (11).

Метод градиентного (или наискорейшего) спуска является достаточно общим и применяется для минимизации любой функции, для которой имеет смысл понятие градиента.

Пусть в некоторой области n -мерного пространства векторов 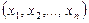задана произвольная функция 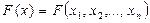. Предположим, что задано начальное приближение 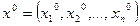к минимуму этой функции. Отправляясь из точки 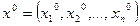, мы хотим двигаться к точке минимума 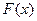как можно быстрее. В силу этого нам нужно двигаться из точки 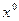в направлении, противоположном направлению вектора-градиента функции 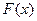в этой точке (вспомним, что 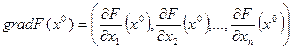- это вектор, по численному значению и по направлению характеризует наибольшую скорость возрастания функции 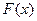в точке 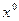). Определив направление движения, необходимо также определить расстояние, на которое нам нужно продвинуться за один шаг.

Путь, по которому мы будем перемещаться из точки 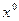, задается уравнением:

, (12)

при этом 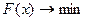. Нам нужно следить за изменением значения 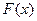при движении в направлении 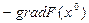, т.е. нужно следить за некоторой функцией

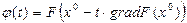. (13)

Остановиться нужно при таком 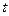, в котором функция 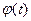достигает своего минимума. Это произойдет там, где 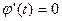(см.матем.анализ – условия локального экстремума функции одной переменной). Пусть 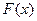определяется по формуле (11). В этом случае

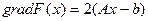. (14)

Формула (14) получается путем непосредственного вычисления координат вектора 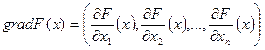и сравненя их значений с соответствующими элементами вектора :

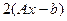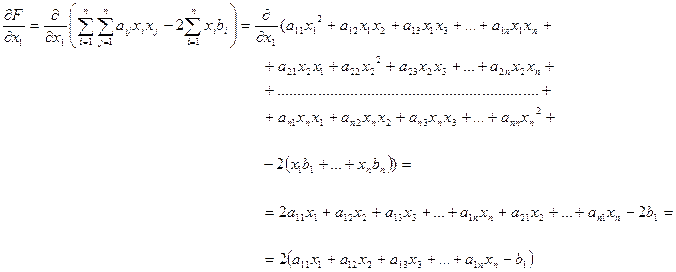
Первая компонента вектора 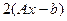получается как удвоенная разность между произведением первой строки матрицы 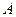на вектор 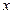и 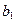, т.е. равна 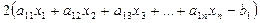, что полностью сопадает со значение, полученным выше для 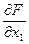. Аналогично проверяются равенства и последующих компонент векторов.

Тогда функция (13) может быть записана в виде:

,

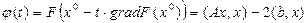где

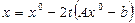. (15)

Вычислим :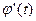

.

;

.

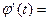
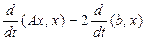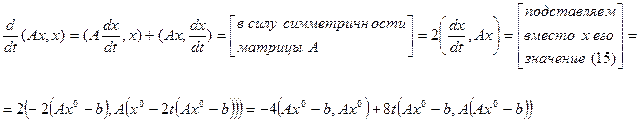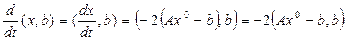Тогда

.

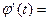
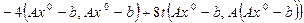Приравнивая 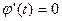, получаем стационарную точку функции:

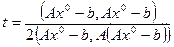. (16)

Алгоритм метода наискорейшего (градиентного) спуска

Пусть 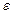- заданная точность (погрешность), с которой нужно получить решение поставленной задачи.

Шаг 1. Задается начальное приближение .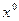

Шаг 2. По формуле (16) вычисляется коэффициент .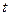

Шаг 3. По формуле (15) вычисляет очередное приближение к решению : .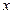

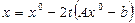Шаг 4 (проверка). Если 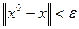, то требуемая точность достигнута, итерационный процесс завершен, в качестве приближенного значения решения СЛАУ (1) берется 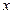, полученный на шаге 3; иначе 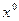полагается равным 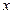, переход на шаг 2.

Замечание 4 (вычислительная сложность метода градиентного спуска). Основные расчетные формулы метода градиентного спуска – это формулы (16) и (15), которые определяет действия данного алгоритма на каждой итерации. Проверьте, что каждая итерация метода градиентного спуска требует 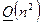операций, тогда в целом количество арифметических операций, необходимых для решения СЛАУ методом градиентного спуска, определиться как

,

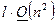где 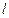- это количество итераций, затраченных в методе градиентного спуска для достижения заданной точности решения .

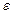Вопросы

1. Сравнение итерационных и прямых методов решения СЛАУ, их принципиальные отличия.
2. Особенности и преимущества итерационных методов решения систем линейных алгебраических уравнений. Основная идея итерационных методов.
3. Критерий сходимости МПИ для любого начального приближения.
4. Вычислительная сложность МПИ.
5. Возможности увеличения скорости сходимости МПИ.
6. Стационарный метод Зейделя как ускорение МПИ.
7. Условия сходимости стационарного метода Зейделя.
8. Вычислительная сложность стационарного метода Зейделя.
9. Основная идея метода наискорейшего спуска. Понятие функционала энергии. Для каких СЛАУ можно использовать метод наискорейшего спуска? Почему?
10. Вычислительная сложность метода наискорейшего спуска.