Интерполяционный многочлен Ньютона и формулы численного дифференцирования

Лекция 18. Численное дифференцирование

План

Задача численного дифференцирования. Основная идея численного дифференцирования

Качественная оценка погрешности численного дифференцирования

Интерполяционный многочлен Ньютона и формулы численного дифференцирования

1. Задача численного дифференцирования. Основная идея численного дифференцирования

К численному дифференцированию приходится прибегать в том случае, когда функция 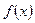, для которой нужо найти производную, задана таблично или же функциональная зависимость 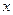и 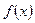имеет очень сложное аналитическое выражение. В первом случае методы дифференциального исчисления неприменимы, а во втором их использование вызывает значительные трудности. В этих случаях вместо 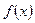рассматривается интерполирующая функция 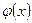, а производную от 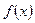приближают производной от 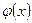. Естественно, что при этом производная от 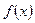будет найдена с некоторой погрешностью. Действительно,

.

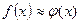Точное равенство будет выглядеть следующим образом:

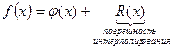(10)

Дифференцируя равенство (10) 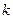раз (в предположении, что 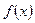и 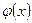имеют производные 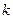-го порядка), получим:

.

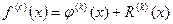Основная идея численного дифференцирования заключается в том, что полагают

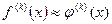. (15)