Качественная оценка погрешности численного дифференцирования

Возникающая в (15) погрешность определяется как

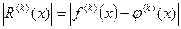. (20)

И хотя при интерполировании в формуле (10) предполагается, что значения малы, из этого в общем случае не вытекает, что малыми будут и значения (см.рис.1). Более того, численному дифференцированию свойственна тенденция увеличивать любую ошибку, присутствующую в исходных данных (в частности, ошибку интерполирования). В силу этого при построении алгоритма решения конкретной прикладной задачи необходимо избегать численного дифференцирования (если это, конечно, возможно).

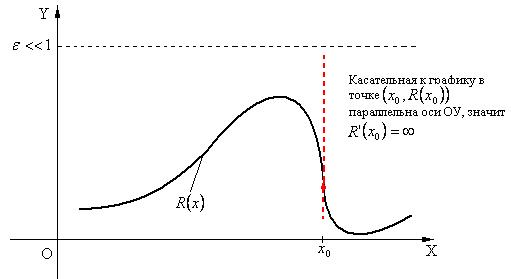
Рис.1.

1. Интерполяционный многочлен Ньютона и формулы численного дифференцирования

Простейшие формулы численного дифференцирования получаем врезультате дифференцирования интерполяционных формул (многочленов). Пусть имеются значения функции в точках 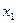,..., , 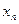требуется найти 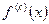. По имеющимся узлам строим интерполяционный многочлен 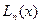, а в соответствии с (15) полагаем

.

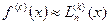Рассмотрим частные случаи. Пусть производная 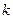-го порядка определяется при дифференцировании интерполяционного многочлена 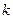-ой степени, построенного по 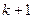узлу интерполяции 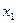,..., . Соответствующий интерполяционный многочлен Ньютона имеет вид (лекц.5):

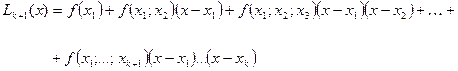
Тогда из

имеем:

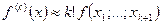. (30)

Пример. Функция 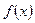задана таблично:

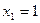
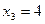
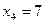
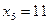
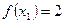
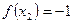
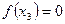
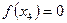
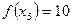
Вычислить 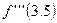. Для вычисления производной третьего порядка в соответствии с формулой (30)

найдем разделенную разность 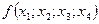третьего порядка, используя для этого таблицу разделенных разностей (см.лекц.5):

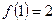
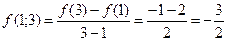
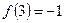
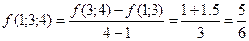
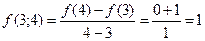
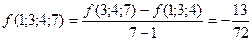
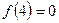
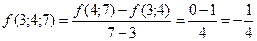
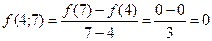
Тогда

.

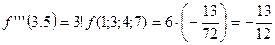Вопросы

1. Когда приходится прибегать к численному дифференцированию?
2. В чем состоит основная идея численного дифференцирования?
3. Формула приближенного значения производной -го порядка.
4. Что происходит при численном дифференцировании с ошибками, присутствующими в исходных данных?
5. Формула интерполяционного многочлена Ньютона.
6. Построение таблицы разделенных разностей.