Метод простой итерации решения системы нелинейных уравнений

Лекция 21. Решение систем нелинейных уравнений

План

Общий вид системы нелинейных уравнений

Метод простой итерации решения системы нелинейных уравнений

Метод Ньютона решения системы нелинейных уравнений, его модификация, уменьшающая вычислительную сложность

Общий вид системы нелинейных уравнений

Система нелинейных уравнений в общем случае имеет вид:

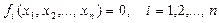. (1)

Функции, определяемые уравнения системы, зависят от 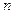неизвестных 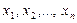. Для возможности существования единственного решения системы (1) количество уравнений в системе совпадает с количеством неизвестных.

Решение системы нелинейных уравнений представляет из себя гораздо более сложную задачу, чем решение одного нелинейного уравнения.

Метод простой итерации решения системы нелинейных уравнений

Система нелинейных уравнений (1) преобразуется к эквивалентному виду:

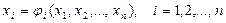(2)

Пусть система (2) в некоторой области пространства 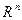имеет единственное решение 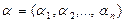, а 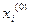- числа, соответственно близкие к 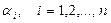. При некоторых ограничениях на функции 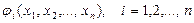, исходя из этих начальных приближений, можно найти приближенные значения 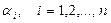, с наперед заданной точностью, используя итерационную формулу, задаваемую методом простой итерации для решения системы нелинейных уравнений:

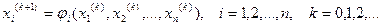(3)

Если

,

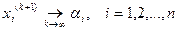то говорят, что метод простой итерации сходится к решению системы (2). Для того, чтобы получить решение с заданной точностью, процесс продолжают до тех пор, пока два последовательные приближения будут отличаться на заданную погрешность.