
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Ньютона решения системы нелинейных уравнений, его модификация, уменьшающая вычислительную сложность
|
|
Рассматривается система уравнений (1). Пусть функции 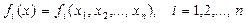 , в некоторой выпуклой области
, в некоторой выпуклой области 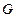 , содержащей решение
, содержащей решение 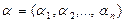 системы (1), имеют непрерывные производные первого порядка и в некоторой окрестности решения
системы (1), имеют непрерывные производные первого порядка и в некоторой окрестности решения 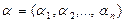 матрица производных первого порядка
матрица производных первого порядка
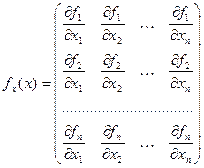 (4)
(4)
является невырожденной.
Обозначим: 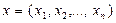 ,
, 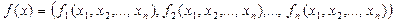 ,
, 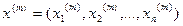 . Последовательность приближений к решению систмы (1) строится по итерационной формуле:
. Последовательность приближений к решению систмы (1) строится по итерационной формуле:
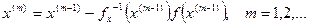 , (5)
, (5)
где 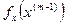 - это числовая матрица, полученная из
- это числовая матрица, полученная из 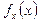 путем вычисления значений производных первого порядка в точке
путем вычисления значений производных первого порядка в точке 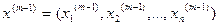 .
.
Формула (5) – это итерационная формула метода Ньютона решения системы нелинейных уравнений (1) (формально она очень напоминает формулу Ньютона для решения одного нелинейного уравнения).
Итерационная формула (5) не очень удобна для вычислений, поскольку требует обращения матрицы производных первого порядка. Для ее упрощения перенесем в (5) 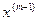 влево с противоположным знаком, и умножим полученную формулу слева на матрицу
влево с противоположным знаком, и умножим полученную формулу слева на матрицу 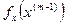 :
:
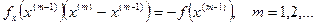 (6)
(6)
Формула (6) – это система линейных алгебраических уравнений относительно неизвестных 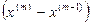 с матрицей
с матрицей 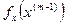 . Ее решение менее вычислительно затратно, чем обращение матрицы. На практике при решении системы нелинейных уравнений методом Ньютона используется именно итерационная формула (6), а не (5).
. Ее решение менее вычислительно затратно, чем обращение матрицы. На практике при решении системы нелинейных уравнений методом Ньютона используется именно итерационная формула (6), а не (5).
Метод Ньютона при решении системы нелинейных уравнений, являясь одним из наиболее быстро сходящихся методов, обладает тем же значительным недостатком, что и для решения одного уравнения: для сходимости метода к решению системы очень важно, чтобы начальное приближение находилось в достаточно малой окрестности точного решения.
Пример. Решить систему нелинейных уравнений
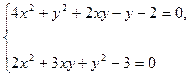
с точностью 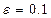 .
.
В наших обозначениях
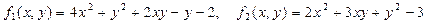 .
.
Точное решение системы: 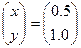 . В качестве начального приближения возьмем
. В качестве начального приближения возьмем 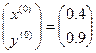 .
.
Матрица производных первого порядка для рассматриваемой системы имеет вид:
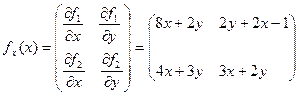 .
.
Для вычисления приближения 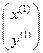 рассмотрим систему уравнений (6) для
рассмотрим систему уравнений (6) для 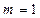 :
:
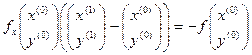 , (7)
, (7)
в которой 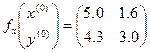 ,
, 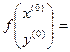
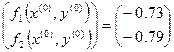 . Если теперь обозначить
. Если теперь обозначить
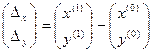 , (8)
, (8)
то система (7) примет вид:
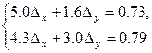
Решая ее, получим: 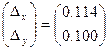 , тогда из (8):
, тогда из (8):
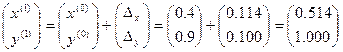 .
.
Сделаем проверку полученного приближения на достижение заданной точности:
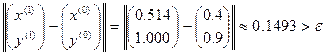 .
.
Проводим следующую итерацию метода Ньютона. Для вычисления приближения 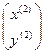 рассмотрим систему уравнений (6) для
рассмотрим систему уравнений (6) для 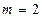 :
:
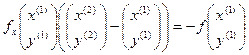 , (9)
, (9)
в которой 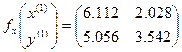 ,
, 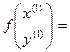
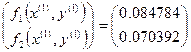 . Снова обозначим для удобства
. Снова обозначим для удобства
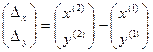 . (10)
. (10)
Система (9) примет вид:
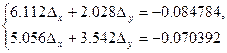
Решая ее, получим: 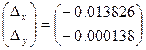 , тогда из (10):
, тогда из (10):
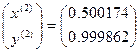 .
.
Сделаем проверку полученного приближения на достижение заданной точности:
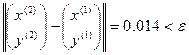 .
.
Точность достигнута, поэтому приближенное решение системы имеет вид:
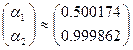 .
.
Вопросы
- Как определяется система нелинейных уравнений?
- Метод простой итерации решения системы нелинейных уравнений.
- Метод Ньютона решения системы нелинейных уравнений. Преимущества и недостатки этого метода.
- Упрощение итерационной фомулы метода Ньютона для решения системы нелинейных уравнений.