Этапы метода конечных разностей

Лекция 35. Метод конечных разностей для решения краевых задач

План

Задача Дирихле.

Этапы метода конечных разностей

Монотонные матрицы. Достаточное условие монотонности матрицы

Задача Неймана

Задача Дирихле

Рассмотрим пример краевой задачи:

Функция 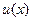ищется на 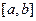, уравнение (1) называется уравнением Гельмгольца, условия (2) – условиями Дирихле, краевая задача (1), (2) называется задачей Дирихле.

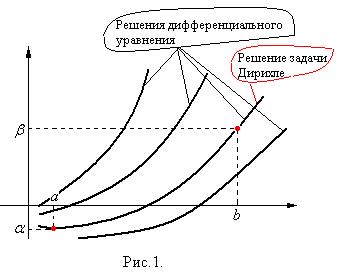
Будем предполагать, что любая краевая задача имеет единственное решение (в отличие от количества решений дифференциального уравнения, которых бесконечно много). Из множества решений дифференциального уравнения выбирается то, которое удовлетворяет условиям (2) (геометрически – проходит через две точки с координатами 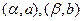(рис.1)).

Этапы метода конечных разностей

Этапы метода конечных разностей (МКР):

Этап 1. Дискретизация области.

Заменяем 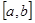набором точек. Они расположены произвольно на 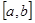и называются узлами сетк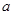и. и 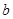- не обязательно узлы. 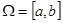, 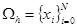. Если 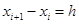одинаково для всех узлов, то сетка называется равномерной, - шаг сетки.

Этап 2. Дискретизация задачи.

Производные, входящие в уравнения, и граничные условия заменяются разностными отношениями по формулам численного дифференцирования.

Обозначим:

.

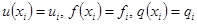Пусть сетка равномерная с шагом (рис.2).

Рис.2.

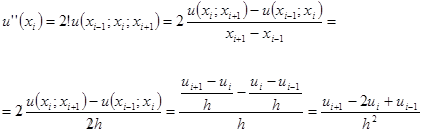
Тогда задача (1), (2) примет вид:

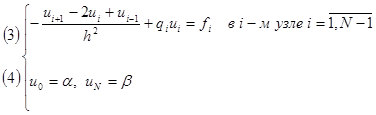
Вместо задачи (1), (2) мы получили дискретную задачу (3), (4) - СЛАУ. Количество уравнений 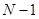. Матрица системы 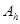и вектор правой части имеют соответственно вид:

.

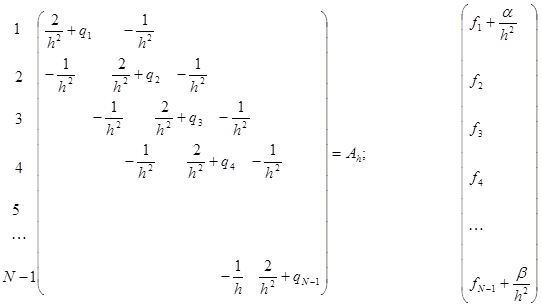Матрица 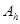- симметричная, трехдиагональная.