Монотонные матрицы. Достаточное условие монотонности матрицы

Займёмся 3 этапом МКР.

Определение. Матрица 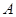обладает свойством монотонности, если из того, что 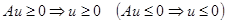. Неравенства понимаются в покомпонентном смысле.

Достаточное условие монотонности матрицы. Пусть для 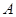выполняются:

1) 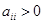для ;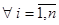

2) ;

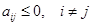3) 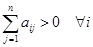(преобладание главной диагонали), тогда 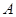обладает свойством монотонности.

Доказательство. Допустим, что это не так, т.е. 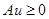, но при этом существует такое 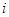, для которого 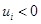. Таких 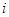может быть несколько. Пусть 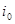такое, что:

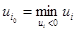
Выпишем :

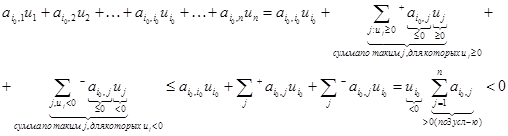
Пришли к противоречию, значит наше допущение ложно.

Лемма 1. Если матрица обладает свойством монотонности, то она невырождена.

Пусть в нашем примере 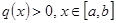. Тогда выполнены все условия:

1) ;

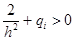2) ;

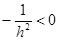3)

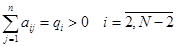
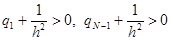
Значит, 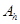- монотонна.ю т.е. и невырождена, следовательно система (3), (4) однозначно резрешима. Этап 3 проведен.

Этап 4.

Лемма 2. Пусть 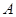обладает свойством монотонности и 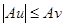. Тогда .

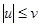Доказательство. Вектор .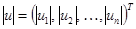

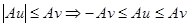. (100)

Левая часть (100):

. (110)

Из правой части (100):

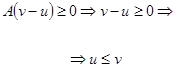(120)

Объединяя заключительные части (110) и (120), получим:

.

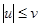Для док-ва этапа 4 построим вектор 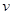, для которого рассмотрим задачу:

,

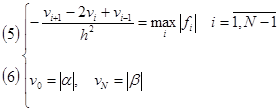Полученную после дискретизации непрерывной задачи

.

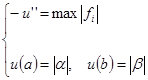Непрерывная задача решается легко. Решением ее очевидно будет многочлен 2-ой степени.

Будем искать 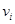в виде многочлена второй степени относительно :

.

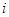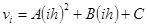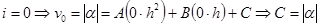
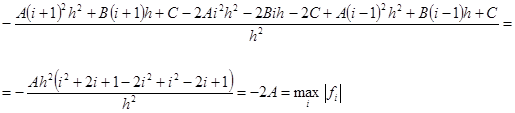
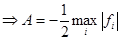
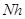- длина всего промежутка, .

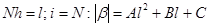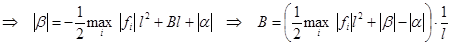
Тогда:

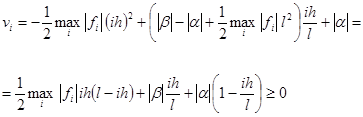
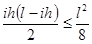
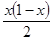( - квадратичная парабол. , )

.

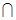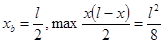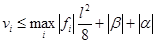Нам надо установить, что: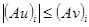

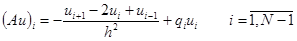
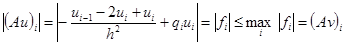
(согласно (5)), т.е. то, что нам нужно. Значит, по лемме 2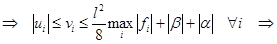

(10) 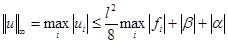это априорная оценка решения.

Эта оценка даёт непрерывную зависимость от входных данных (правой части и граничных условий) для дискретной задачи.

Действительно

(11) 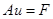(т.к. это уже не 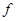, мы перебрасываем сюда и ).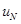

(11) - это исходная задача.

Рассмотрим возмущенную задачу:

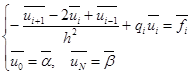здесь мы изменили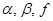

Матричная запись: (12)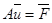

(11)-(12)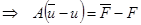

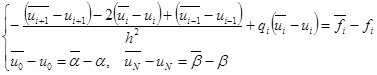
Матрица в (13) сохранилась.

Для решения (13) используем оценку (10):

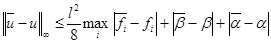
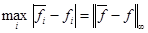
Если мало менять входные данные, то мало меняется и решение; получаем непрерывную зависимость решения от входных данных. Т.е. мы получили корректность дискретной задачи.

5 этап. У дифференциальной задачи решением будет некоторая кривая (рис.3).

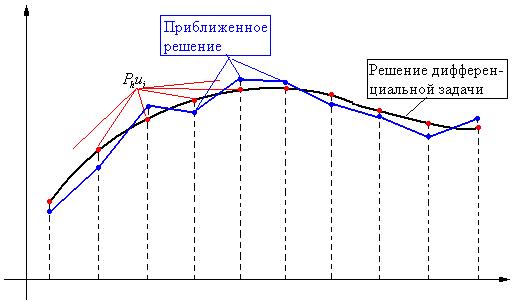
Рис. 3.

Мы ищем приближенное решение – вектор (набор чисел в узлах сетки). Эти точки вообще не лежат на кривой. Мы должны сравнить - решение дифференциальной задачи и вектор .

Для того, чтобы разность 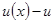приобрела какой-то смысл, можно провести дискретизацию решения, т.е. вычислить некоторую функцию .

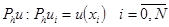Теперь у нас два вектора. Если 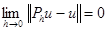, то решение разностной задачи сходится к решению дифференциальной.

Можно понимать сходимость и по-другому: доопределить (восполнить) вектор 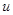до функции, заданной на 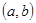(например, построить сплайн).

Обозначим оператор восполнения через 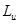. 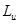- функция, определенная на 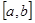. Если 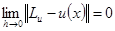, то решение разностной задачи сходится к решению дифференциальной задачи.

Проведем дискретизацию решения дифференциальной задачи:

.

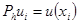Вычислим:

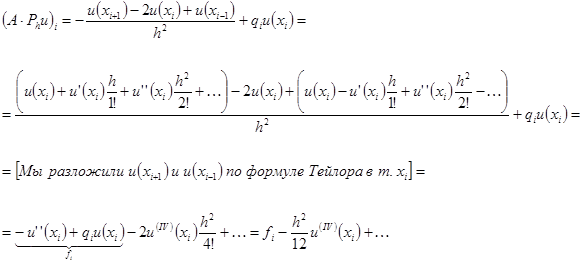
Правая часть получила возмущение порядка 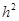, 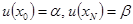- не изменились.

Рассмотрим 2 задачи: 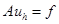- разностная задача, 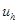- вектор решения разностной задачи.

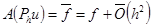
В силу оценки (10) .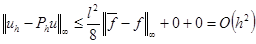

Т.е. мы доказали:

Теорема. Решение разностной задачи сходится к решению дифференциальной в смысле 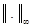, причем скорость сходимости равна .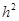