Аппроксимация на решениях уравнения

Лекция 36. Повышение порядка аппроксимации граничных условий

План

Изменение расположения узлов сетки

Аппроксимация на решениях уравнения

Смешанная краевая задача для уравнения Гельмгольца

Пример краевой задачи для уравнения Гельмгольца в двумерном случае

Изменение расположения узлов сетки

До настоящего момента рассматривалась равномерная сетка, а концы сегмента считались узлами. Теперь изменим результат дискретизации области: равномерность сохраним, но концы будут находиться посредине между узлами (рис.1).

Рис.1.

Уравнения сохраняются, а порядок аппроксимации граничных условий увеличивается на 1:

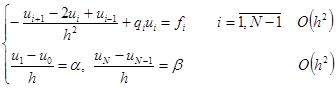
Действительно:

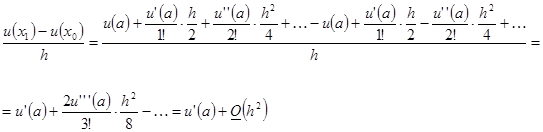
Аппроксимация на решениях уравнения

Дискретизация области соответствует рис.2 (равномерная сетка, концы сегмента являются узлами).

Рис.2.

Как было получено ранее

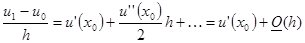
или

.

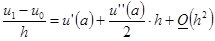Если удастся убрать слагаемое 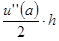, то получим порядок аппроксимации .

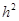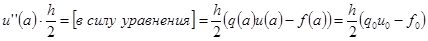
(если предположить, что 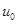- решение уравнения в т. ).

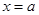Тогда

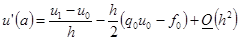
Тогда первое граничное условие:

.

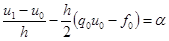Это два хороших способа. Матрица практически сохраняет свои свойства. Существуют еще способы повышеня порядка аппроксимации граничных условий:

1) Использование большего количества узлов для аппроксимации граничных условий. Например, вместо 2-х узлов взять 3 или 4. Но при этом портится матрица системы.

2) Использование неравномерной сетки. В окрестности граничной точки мы сгущаем сетку. Это не очень удобный способ.