Основная классификация численных методов решения систем линейных алгебраических уравнений

Численные методы решения систем линейных алгебраических уравнений (СЛАУ), общий вид которых

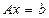, (5)

где 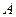- матрица системы, 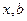- вектор неизвестных и правой части соответственно, делятся на два больших класса: прямые (или точные) и итерационные (или приближенные).

Далее будем рассматривать неоднородные системы с квадратными вещественными матрицами: , .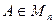

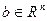Точные методы – это методы, которые в предположении отсутствия округлений дают точное решение СЛАУ после конечного, определяемого заранее числа арифметических операций.

Итерационные методы – это методы, которые в предположении отсутствия округлений дают, в общем случае, точное решение СЛАУ после бесконечного числа операций. Их общая идея заключается в следующем: по заданной матрице системы 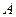, вектору правой части 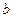и некоторому начальному приближению 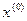к решению СЛАУ находится следующее приближение 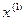, по которому на следующем шаге строится приближение 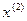к решению и т.д. Получаем бесконечную векторную последовательность 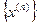приближений к решению: 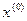, ,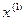..., ,...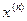. Итерационный процесс строится таким образом, чтобы 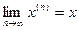. В этом случае говорят о сходящемся итерационном процессе. Таким образом, искомое решение – это предел последовательности приближений, а значит может быть получен только за бесконечное число шагов.

Более подробно отличия прямых и итерационных методов будут рассмотрены в теме «Итерационные методы решения СЛАУ».