Вычислительная сложность метода Гаусса с частичным выбором главного элемента

Лекция 9. ВЫЧИСЛИТЕЛЬНАЯ СЛОЖНОСТЬ ПРЯМЫХ МЕТОДОВ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

1. Вычислительная сложность метода Гаусса с частичным выбором главного элемента.
2. Вычислительная сложность метода Гаусса с полным выбором главного элемента.
3. Сравнение методов Гаусса с частичным и полным выбором главного элемента по точности и вычислительной сложности.
4. Вычислительная сложность метода, основанного на LU-разложении матрицы системы. Сравнение LU-метода и метода Гаусса

Вычислительная сложность метода Гаусса с частичным выбором главного элемента

Пусть необходимо решить СЛАУ

. (5)

Выбор главного элемента перед исключением в первом столбце матрицы СЛАУ осуществляется в области, ограниченной красным цветом на рис.1, между элементами первого столбца. Для такого выбора потребуется провести 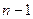операцию сравнения.

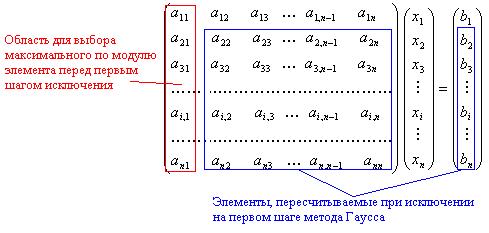
Рис.1.

После выбора главного элемента и перестановки соответствующих строк матрицы и соответствующих элементов вектора правой части (это подробно описано в лекции 8), осуществляется пересчет элементов матрицы и вектора правой части, стоящих после перестановки на позициях, ограниченных синим цветом на рис.1. Количество этих элементов - 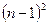в матрице СЛАУ и 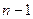в векторе правой части. Пересчет каждого элемента матрицы на 1-м шаге исключения происходит в соответствии с формулой (формула (5) лекции 8):

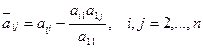, (10)

здесь 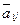- элементы матрицы СЛАУ после 1-го шага исключения (аналогичной будет формула для пересчета элементов вектора правой части), т.е. требует 3 арифметических операций – 1 умножение, 1 деление, 1 вычитание. Тогда на весь пересчет при первом шаге исключения Гаусса потребуется 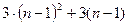арифметических операций.

Суммарно на первый шаг метода Гаусса будет затрачено:

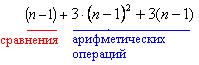
Перед проведением исключений во втором столбце матрицы СЛАУ (второй шаг метода Гаусса) выбор главного элемента осуществляется в области, ограниченной красным цветом на рис.2, между 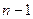элементом второго столбца. Для такого выбора потребуется провести 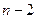операции сравнения.

Рис.2.

После выбора главного элемента и перестановки соответствующих строк матрицы и соответствующих элементов вектора правой части, осуществляется пересчет элементов матрицы и вектора правой части, стоящих после перестановки на позициях, ограниченных синим цветом на рис.2. Количество этих элементов - 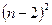в матрице СЛАУ и 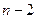в векторе правой части. Пересчет каждого элемента матрицы на 2-м шаге исключения происходит в соответствии с формулой (10): 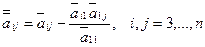, здесь 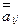- элементы матрицы СЛАУ после 2-го шага исключения (аналогично для пересчета элементов вектора правой части). Тогда на весь пересчет при втором шаге исключения Гаусса потребуется 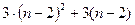арифметических операций. Суммарно на второй шаг метода Гаусса будет затрачено:

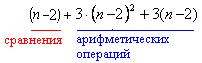
И т.д. Перед проведением исключений в 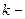столбце матрицы СЛАУ для выбора главного элемента потребуется провести 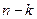операций сравнения. Пересчет при исключении коснется 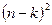элементов в матрице СЛАУ и 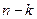элементов в векторе правой части, для чего потребуется 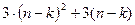арифметических операций. Суммарно на 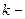ый шаг метода Гаусса будет затрачено:

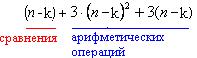
Всего для прямого хода метода Гаусса при решении СЛАУ размерами 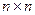потребуется 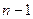шаг ((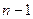)-ый шаг отвечает исключению в 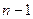-ом столбце матрицы СЛАУ). Учитывая это, можем посчитать полное количество операций для проведения прямого хода метода Гаусса:

Шаг прямого хода метода Гаусса	Количество сравнений для выбора главного элемента	Количество операций для пересчета элементов матрицы и вектора правой части
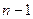
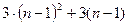
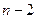
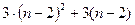
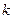
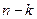
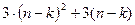
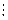
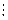
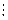
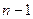
		3+3
ВСЕГО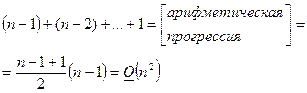
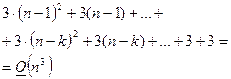
Полное количество операций для проведения прямого хода метода Гаусса:

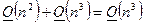
Итак, общее количество операций для проведения прямого хода метода Гаусса:

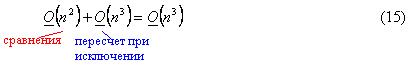
Результатом прямого хода метода Гаусса является эквивалентная исходной система с верхней треугольной матрицей:

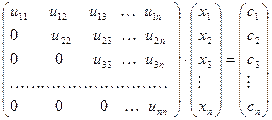. (20)

Решение полученной СЛАУ осуществляется снизу вверх при помощи последовательной подстановки (обратный ход метода Гаусса). Определим вычислительную сложность обратного хода.

Из последнего уравнения СЛАУ (20):

,

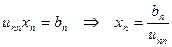Т.е. для вычисления 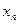понадобится 1 арифметическая операция.

Из предпоследнего уравнения СЛАУ (20), имея уже вычисленное на предыдущем шаге значение 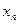, получаем:

,

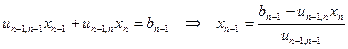Т.е. для вычисления 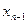понадобится 3 арифметических операции. И т.д. Для вычисления 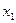из 1-го уравнения СЛАУ (20):

Потребуется 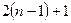арифметических операции. Тогда общее количество операций для решения СЛАУ с треугольной матрицей (обратный ход метода Гаусса) будет определяться как:

.

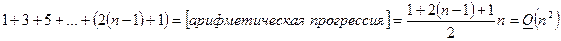Таким образом, вычислительная сложность метода Гаусса с частичным выбором главного элемента решения СЛАУ размером 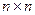равна 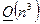: