На прямоугольной площадке

Пусть нагрузка р распределена на площадке с размерами b, l (рис. 3.2). Тогда напряжения в любой точке основания можно определить аналогично формуле (3.2), приняв элементарную вертикальную нагрузку в виде dF = p· dx· dy и заменив суммирование интегрированием по площади. В итоге напряжение определяется по простой формуле:

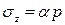, (3.3)

где α – коэффициент рассеяния напряжений с глубиной, зависящий от положения рассматриваемой точки и формы загруженной площадки.

Например, для точки на вертикали под центром площадки α есть функция двух безразмерных параметров 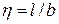и 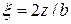(табл. 3.2). С использованием табл. 3.2, задаваясь глубиной z, легко построить эпюру σ _z.

d F = p· dx· dy   Рис. 3.2. dx Y X b	Рис. 3.3. 1 – эпюра σ Z; 2- изобара σ Z X p 0, 1p 0, 2p 0, 5p 0, 8p

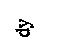
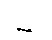
Напряжения по вертикали, проходящей через угловую точку, легко определить, используя эту же таблицу.

Известно, что напряжение под углом в точке на глубине 2z равно одной четвертой осевого вертикального напряжения на глубине z. То есть, определив по табл. 3.2. значение α для 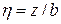, напряжение в точке под углом на глубине 2z получим по формуле: .

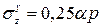Таблица 3.2

2z/b	Круг	Значения α для прямоугольной площадки при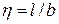
1, 0	1, 4	1, 8	2, 4	3, 2		Полоса l/b> 10
	1, 000	1, 000	1, 000	1, 000	1, 000	1, 000	1, 000	1, 000
0, 4	0, 949	0, 960	0, 972	0, 975	0, 976	0, 977	0, 977	0, 977
0, 8	0, 756	0, 800	0, 848	0, 866	0, 876	0, 879	0, 881	0, 881
1, 2	0, 547	0, 606	0, 682	0, 717	0, 739	0, 749	0, 754	0, 755
1, 6	0, 390	0, 449	0, 532	0, 578	0, 612	0, 629	0, 639	0, 642
2, 0	0, 285	0, 336	0, 414	0, 462	0, 505	0, 530	0, 545	0, 550
2, 4	0, 214	0, 257	0, 325	0, 374	0, 419	0, 449	0, 470	0, 477
2, 8	0, 165	0, 201	0, 260	0, 304	0, 349	0, 383	0, 410	0, 420
3, 2	0, 130	0, 160	0, 210	0, 251	0, 294	0, 329	0, 360	0, 374
3, 6	0, 106	0, 131	0, 173	0, 209	0, 250	0, 285	0, 319	0, 337
4, 0	0, 087	0, 108	0, 145	0, 176	0, 214	0, 248	0, 285	0, 306
4, 4	0, 073	0, 091	0, 123	0, 150	0, 185	0, 218	0, 255	0, 280
5, 2	0, 053	0, 067	0, 091	0, 113	0, 141	0, 170	0, 208	0, 239
6, 0	0, 040	0, 051	0, 070	0, 087	0, 110	0, 136	0, 173	0, 208

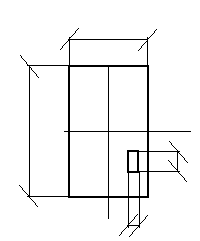
Напряжения в любых точках основания, не лежащих на центральной и угловых вертикалях, определяются по способу угловых точек. После определения напряжений в ряде точек напряженное состояние основания можно наглядно охарактеризовать изолиниями равных напряжений (изобарами, рис. 3.3). Все они проходят через угловые точки площадки, которые здесь (как и точка приложения сосредоточенной нагрузки на рис. 3.1) являются особыми точками.