Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы Зейделя и Ньютона для решения уравнений УР.
|
|
Метод Зейделя относится к простейшему итерационному методу решения систем линейных уравнений УР. Рассмотрим простую итерацию для понимания сути применения итерационных методов.
Рассмотрим систему уравнений узловых напряжений третьего порядка:
 (1)
(1)
Предполагая, что диагональные элементы не равны 0, разрешим первое Ур-е системы относительно U1, второе – относительно U2, третье – относительно U3. Получим эквивалентную (1) систему:
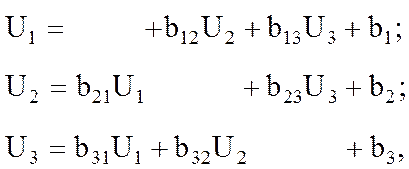 (2)
(2)
где 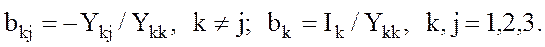 Зададим начальные приближения неизвестных
Зададим начальные приближения неизвестных 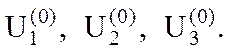 Подставим их в правые части (2), получаем первые приближения
Подставим их в правые части (2), получаем первые приближения 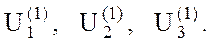 Вычисление первого приближения неизвестных соответствует первому шагу итерационного процесса. Полученные i-е приближения используются для расчёта последующих (i+1)-х приближений.
Вычисление первого приближения неизвестных соответствует первому шагу итерационного процесса. Полученные i-е приближения используются для расчёта последующих (i+1)-х приближений.
 (3)
(3)
Введём матрицу и вектор-столбцы:
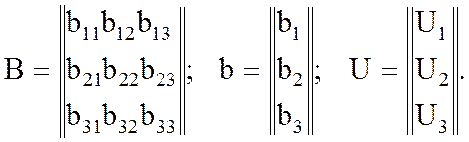
Диагональные элементы матрицы В равны 0, а недиагональные совпадают с коэффициентами систем (2) или (3). Учитывая правило умножения матриц запишем системы (2) и (3) в матричной форме:
 (4)
(4)
Элементы матрицы В – безразмерные величины, а элементы вектора b имеют размерность напряжения.
Итерационный процесс, определяемый выражением (3) или (4), называется простой итерацией.
Метод Зейделя представляет собой незначительную модификацию простой итерации. Отличие заключается в том, что найденное (i+1)-е приближение (k-1)-го напряжения 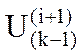 сразу же используется для вычисления следующего, k-го напряжения
сразу же используется для вычисления следующего, k-го напряжения 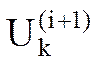 . Таким образом для (1) итерационный процесс метода Зейделя описывается след. выражением:
. Таким образом для (1) итерационный процесс метода Зейделя описывается след. выражением:
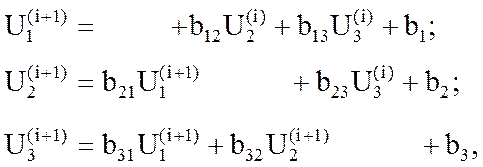 (5)
(5)
По методу Зейделя (i+1)-е приближение k-го напряжения 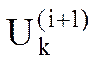 вычисляется так:
вычисляется так:
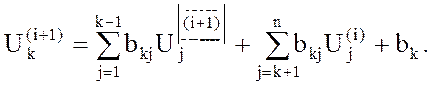 (6)
(6)
Применение метода Зейделя для решения нелинейных ур-й узловых напряжений аналогично (6).
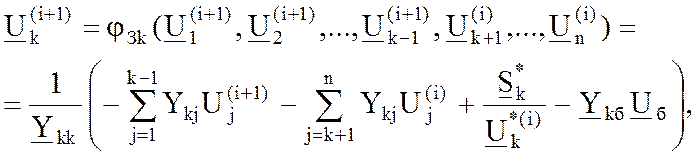 (7)
(7)
где 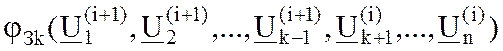 - нелинейная функция, описывающая итерационный процесс Зейделя.
- нелинейная функция, описывающая итерационный процесс Зейделя.
В расчётах на ЭВМ при замене комплексных переменных на действительные по методу Зейделя определяются активные и реактивные напряжения узлов:
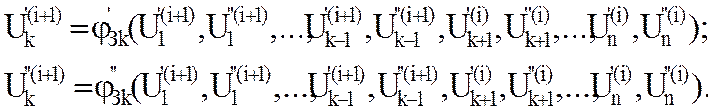 (8)
(8)
где 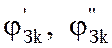 - составляющие комплексной нелинейной ф-ии
- составляющие комплексной нелинейной ф-ии 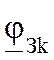 , описывающей итерационный процесс Зейделя.
, описывающей итерационный процесс Зейделя.
Сходимость метода Зейделя к решению нелинейных уравнений УР медленная. Для ускорения сходимости применяют ускоряющие коэффициенты, или метод неполной релаксации.
Обозначим 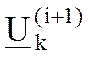 напряжение k-го узла, определённое на (i+1)-ом шаге по обычным итерационным формулам (7). Ускоренное (i+1)-е приближение значения напряжения k-го узла
напряжение k-го узла, определённое на (i+1)-ом шаге по обычным итерационным формулам (7). Ускоренное (i+1)-е приближение значения напряжения k-го узла 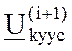 определяется по формуле
определяется по формуле 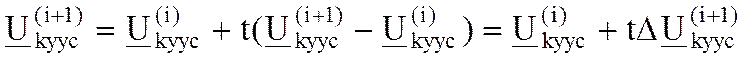 где
где 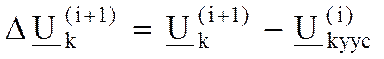 - поправка по напряжению k-го узла на (i+1)-м шаге; t – ускоряющий коэффициент. Напряжение
- поправка по напряжению k-го узла на (i+1)-м шаге; t – ускоряющий коэффициент. Напряжение 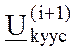 , вычисленное с ускорением, принимается в качестве исходного при расчёте следующего, (i+2)-го шага.
, вычисленное с ускорением, принимается в качестве исходного при расчёте следующего, (i+2)-го шага.
В случае t=1 получим обычный итерационный процесс метода Зейделя.
Основные достоинства метода: лёгко программируется и требует малой оперативной памяти.
Недостаток – в медленной сходимости. Особенно плохо сходится (в ряде случаев даже расходится) при расчёте УР систем с устройствами продольной компенсации, с трёхобм. трансформаторами и автотранс. и др.
Метод Ньютона.
Данный метод пригоден для решения обширного класса нелинейных ур-й.
Идея метода состоит в послед. замене на каждой итерации сис-мы нелин. ур-й некоторой лин. сис-мой, решение которой даёт более близкие к решению нелинейной сис-мы значения неизвестных, чем исходное приближение. Поясним идею на примере решения ур-я
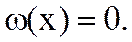 (1)
(1)
Решение ур-я точка 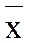 , в которой кривая
, в которой кривая 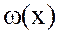 проходит через 0. Зададим начальное приближение
проходит через 0. Зададим начальное приближение 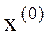 . Заменим (1) в окрестности точки
. Заменим (1) в окрестности точки 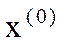 линейным уравнением
линейным уравнением
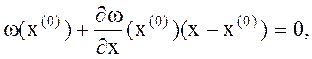 (2)
(2)
левая часть – два первых члена разложения ф-ии  в ряд Тейлора. Решив (2), определим поправку к начальному приближению:
в ряд Тейлора. Решив (2), определим поправку к начальному приближению:
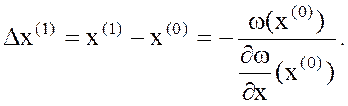 (3)
(3)
За новое приближение неизвестного примем
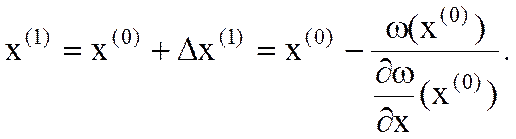 (4)
(4)
Аналогично определяем следующие приближения:
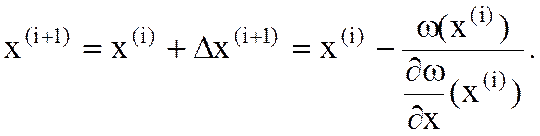
Итерационный процесс сходится, если 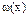 становится близкой к нулю или
становится близкой к нулю или
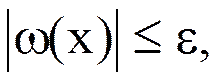 (5)
(5)
где 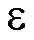 - заданная величина невязки.
- заданная величина невязки.
Геометрическая интерпретация
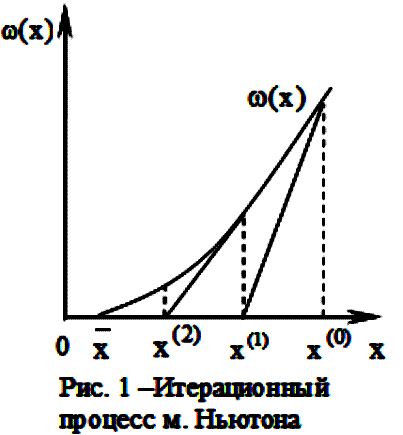
Один шаг метода Ньютона сводится к замене кривой 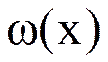 на прямую
на прямую
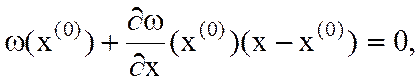 которая является касательной к этой кривой в
которая является касательной к этой кривой в
точке  . Поэтому метод наз-ют также методом касательных.
. Поэтому метод наз-ют также методом касательных.
Приближение 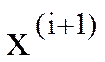 - точка пересечения касательной к кривой
- точка пересечения касательной к кривой 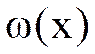
в точке 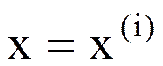 с осью x.
с осью x.
Сис-ма нелинейных ур-й с действительными переменными:
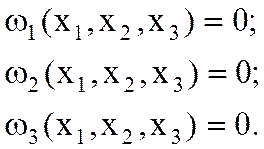 (6)
(6)
Запишем в матричной форме
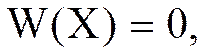 (7)
(7)
где 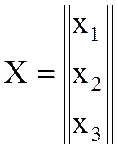 - вектор-столбец;
- вектор-столбец; 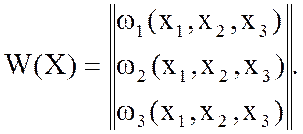 - вектор функция.
- вектор функция.
Матрица Якоби (матрица производных сис-мы ф-ий 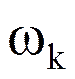 по переменным
по переменным 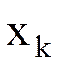 ):
):

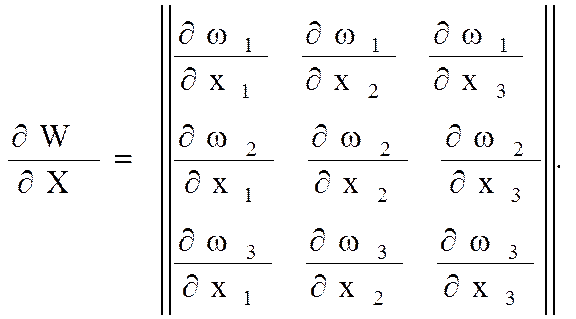 (8)
(8)
Сис-ма линеаризованных ур-й в матричном виде:
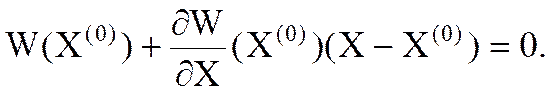 (9)
(9)
Решение узловых ур-й баланса мощности для к-го узла:
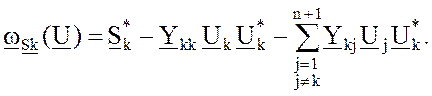 (10)
(10)
Уравнения баланса мощностей для k-го узла при переменных U и 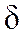 :
:
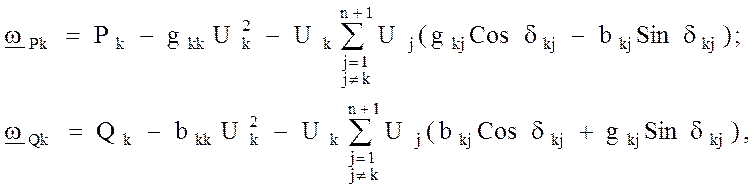 где
где 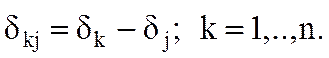
Матрица Якоби:
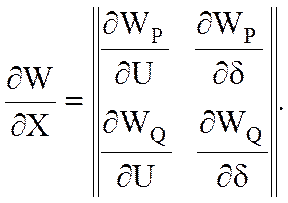
т.е элементы матрицы – это частные производные небалансов активной и реактивной мощностей по модулям и фазам напряжений узлов.
Решение ур-й узловых напряжений баланса токов для к-го узла:
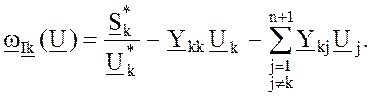
Элементы матрицы Якоби – это производные активных и реактивных небалансов токов по активным и реактивным напряжениям узлов.
Таким образом, метод ньютона в расчёте УР сходится быстрее и надёжнее метода Зейделя. Но он требует больше памяти при расчёте на ЭВМ, чем метод Зейделя.
2- 4. Регулирование напряжения в электрических сетях. Компенсация реактивной мощности.