
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Применение метода Лагранжа для решения задачи оптимального распределения потоков мощности в сети
|
|
Метод состоит в определении минимума функции Лагранжа, в которую входят Δ Р и уравнения первого закона Кирхгофа, каждое из которых умножается на соответствующий множитель Лагранжа.
Рассмотрим задачу ОРС предыдущего примера когда потоки реактивной мощности Qkj = 0. Равенство нулю потоков Q в линиях 12, 23, 13 означает, что в узлах 2 и 3 имеет место полная компенсация реактивной мощности.
Вид задачи: определить:
Минимум 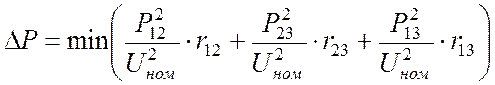 (11)
(11)
при выполнении
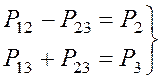 (12)
(12)
Функция Лагранжа
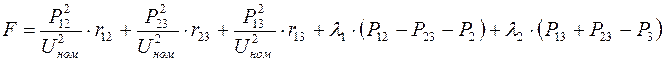
где λ 1, λ 2 – множители Лагранжа.
Задача на условный экстремум (11) (12) с тремя переменными Р12, Р23, Р13 сведена к определению безусловного (минимума) функции Лагранжа (13), которая зависит от пяти переменных: трех потоков мощности и двух множителей Лагранжа.
Минимум функции Лагранжа соответствует решению исходной задачи и определения равенства нулю пяти частных производных:
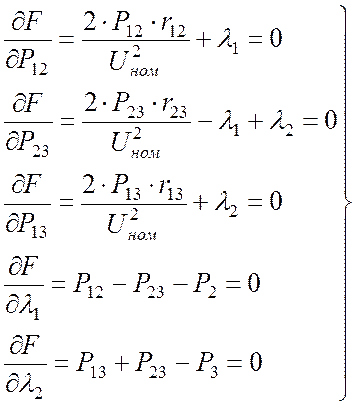 (14)
(14)
Для решения линейных алгебраических уравнений преобразуем ее правые три уравнения второго закона Кирхгофа, исключив из них множители Лагранжа:
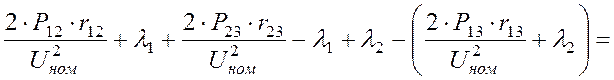
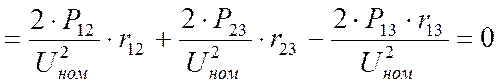
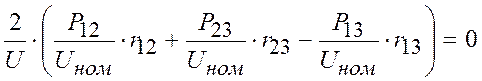
т.е. 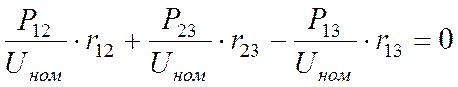 (15)
(15)
Получили выражение аналогичное
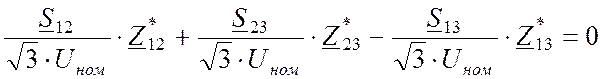
что для простой замкнутой сети, только наше выражение с r вместо Z и при Q = 0. Далее решаем 4 и 5 уравнения системы (15)
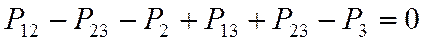
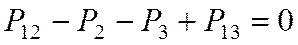
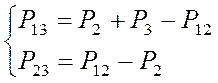
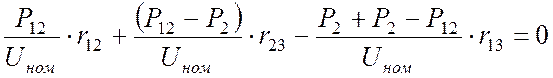
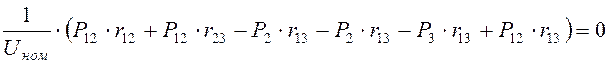
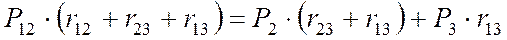
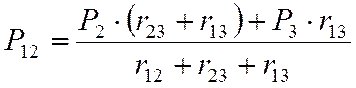 , т.е (10)
, т.е (10)
Оба метода дают одинаковое решение.
Как правило решение задачи оптимизации находит в результате численного решения системы уравнений, соответствующей условию минимума функции Лагранжа.