Уравнения несимметричных режимов в фазных и симметричных координатах

Для анализа несимметричных режимов можно приме­нять как метод симметричных составляющих, так и систе­му фазных координат. При расчете в фазных координатах напряжения и токи в любом месте сети содержат соответ­ствующие фазные значения:

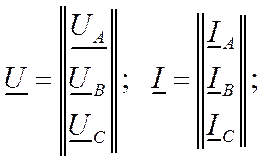
Рассмотрим уравнение режима для схемы участка грехфазной линии, каждая фаза которой характеризуете некоторым активным сопротивлением, сопротивлением самоиндукции, а также взаимной индуктивностью, имеющей место между данной и двумя другими фазами. Для рассматриваемого участка линии (рис. 11.2) справедливы уравнения

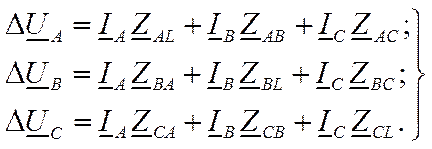
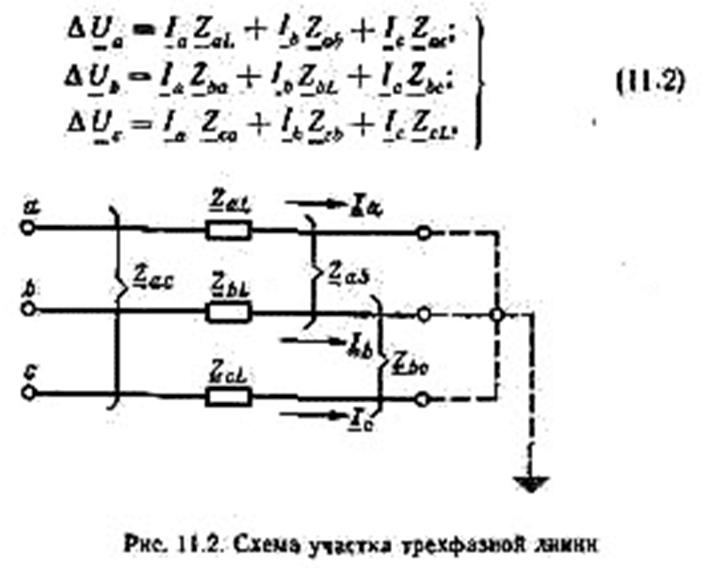
или в матричной форме

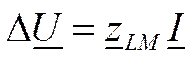
В уравнениях (11.2) и (11.3)

и матрица сопротивлений участка линии в фазных координатах

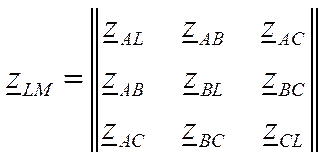
Симметричный режим участка линии на рис. 11.2 описывается одним уравнением (закон Ома)

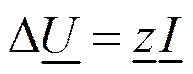где I— ток в линии; Z — сопротивление участка симметричной линии; U—падение напряжения в сопротивлении Z.

Действительно, если равны сопротивления фаз и взаим­ные индуктивности между ними, при симметричной систе­ме фазных токов система уравнений (11.2) может быть заменена одним уравнением (11.5). Сравнивая (11.2) и (11.5), легко убедиться, что несимметричный режим участ­ка линии на рис. 11.2 описывается системой трех линейных уравнений вместо одного уравнения для симметричного режима. Это положение можно распространить и на слож­ную электрическую сеть с п независимыми узлами. Ре­жим такой сети можно рассчитать, если решить обычные линейные уравнения узловых напряжений

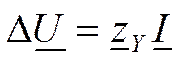где размерность векторов падения напряжения AU, токов в узлах I и матрицы собственных и взаимных узловых со­противлений равна 3n, где n - число независимых узлов.

При расчете несимметричного режима в фазных коор­динатах каждый элемент, например вектор узловых токов I, определяется (11.1), т. е. содержит комплексы фазных токов. Соответственно каждый элемент матрицы Z _Y опреде­ляется (11.4), т. е. содержит активные сопротивления, а также сопротивления самоиндукции и взаимоиндукции.

Расчет несимметричного режима в фазных координатах не применялся до использования ЭВМ, так как приводил к трехкратному увеличению размерности решаемой системы. В настоящее время у нас в стране и за рубежом разраба­тываются методы расчета несимметричных режимов на ЭВМ в фазных координатах.

Однако наибольшее распространение как до примене­ния ЭВМ, так и в настоящее время получили расчеты не­симметричных режимов с помощью метода симметричных составляющих.

При использовании метода симметричных составляю­щих параметры режима определяются в системе коорди­нат симметричных составляющих. Сущность метода сим­метричных составляющих заключается в представлении любой трехфазной несимметричной системы величин в ви­де суммы трех симметричных величин. На рис. 11.3 изо­бражены три симметричные системы применительно к рас­чету тока.

Токи фаз b и с можно выразить через ток фазы а следующим образом:

для прямой последовательности (рис. 11.3, а)

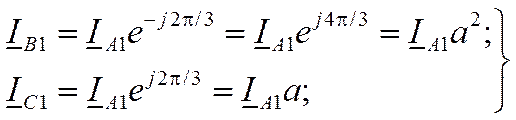
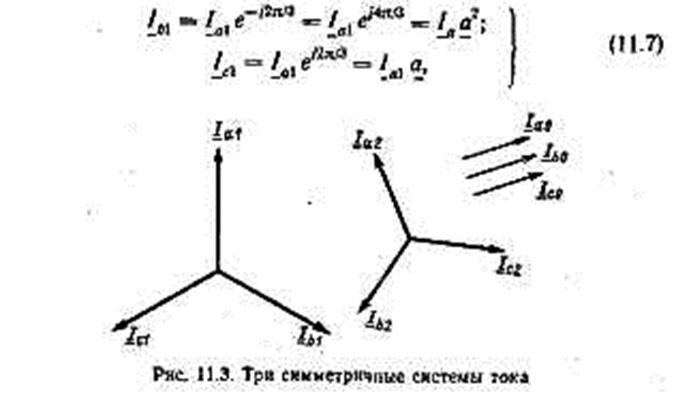
для обратной последовательности (рис. 11.3, б)

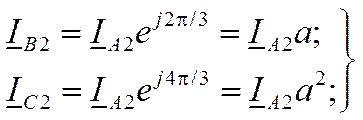
В соответствии с методом симметричных составляющих с учетом (11.7) и (11.8) трехфазную несимметричную, систему токов 1 в выражении (11.1) можно представить в виде суммы трех симметричных величин:

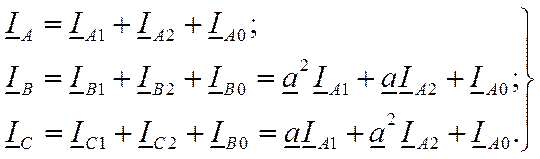
В матричной форме уравнения (11.9) имеют вид

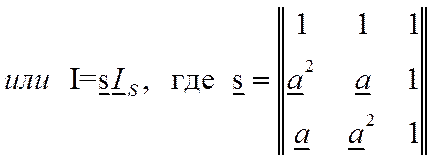
Матрица s определяет переход от системы координат симметричных составляющих к системе фазных координат. Данная матрица имеет обратную:

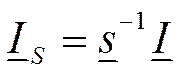
Из (11.10) получим

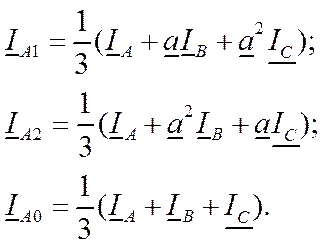
Систему (11.12) можно легко получить, если решить уравнения (11.9). Матрица s ^-1, а также выражения (11.11) или (11.12) отражают переход из фазных координат в сим­метричные.

Покажем, как с помощью матриц преобразования s и s ^-1получить в системе координат симметричных составля­ющих уравнения закона Ома (11.2) или (11.3), ранее по­лученные в системе фазных координат.

Переход от системы симметричных составляющих к фазным координатам (11.10) справедлив и для таких па­раметров режима, как напряжение и падение напряжения/

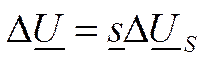
С учетом (11.10) и (11.13) выражение (11.3) можно записать в следующем виде в системе симметричных координат:

Отсюда следует, что

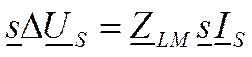
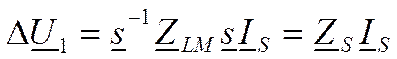
где матрица сопротивления участка линии в системе симметричных координат Z_s определяется по матрице сопротивлений в фазных координатах ZLM таким выражением:

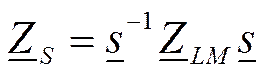
По выражению, аналогичному (11.16) можно найти и другие пассивные параметры сети, например проводимости ветвей в системе симметричных координат.

Система уравнений (11.15) имеет ту же размерность, что и (11.3). Поэтому в общем случае при учете различных взаимных междуфазных индуктивностей, различных фазных активных сопротивлений и сопротивлений самоиндукции применение симметричных составляющих не приводит к понижению размерности систем уравнений, решаемых при расчете установившегося режима. Более того, в этом общем случае приходится дополнительно определять сопротивления в симметричных координатах по выражению (11.16). Таким образом, параметры элементов сети иногда проще определяются в системе фазных координат. Достоинство, метода симметричных составляющих в том, что с го помощью проще определяются показатели несимметрии составляющие обратной и нулевой последовательностей напряжений и токов. Это важно, поскольку для проверки требований по качеству напряжения в соответствии с ГОСТ необходимо вычислить эти показатели несимметрии. Второе достоинство метода симметричных составляющих в том, что с его помощью в некоторых случаях можно выполнять расчет составляющих обратной последовательности с большей точностью, чем в фазных координатах.

Составляющие обратной последовательности в таких случаях имеют небольшую величину, поэтому определение их по результатам расчета в системе фазных координат.

связанное с вычитанием близких величин, может привести к заметному понижению точности расчета.

Основное преимущество метода симметричных состав­ляющих состоит в понижении размерности решаемой системы уравнений при расчете установившегося режима в частном, но практически важном случае, когда равны взаимные междуфазные индуктивности, а также и фазные активные сопротивления и сопротивления самоиндукции. Например, при исследовании режимов, вызванных несим­метричными нагрузками, можно не считаться с различием сопротивлений взаимной индукции между фазами и при­нять собственные сопротивления фаз одинаковыми.

В этом случае в (11.4) Z L= Z aL*= Z _bL= Z _CL — собствен­ные сопротивления фаз; Z _M= Z _ba = Z _ac= Z _ca = Z _bc = =Z_cb=Z_ab, — среднее взаимное сопротивление фаз. " При этом из (11.16), (11.14) следует

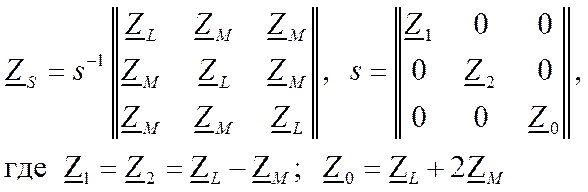
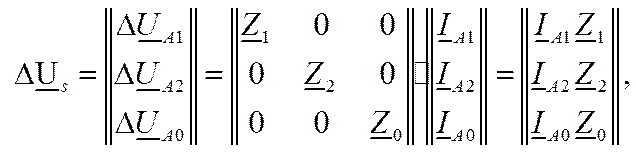
Из (11.20) следует, что в рассматриваемом частном случае вместо системы из трех уравнений (11.15) можно решать независимо по уравнению для каждой последова­тельности, т. е. порядок решаемой системы понижается в 3 раза. Иными словами, падение напряжения всех трех по­следовательностей определяется в рассматриваемых усло­виях только токами тех же последовательностей и, следо­вательно, режим определяется не системой уравнений, какв общем-случае (11.15), а тремя независимыми уравнения­ми и (11.20).

Сопротивлениями прямой, обратной и нулевой последо­вательностей называют коэффициенты пропорциональнос­ти между падением напряжения и током одной и той же поледовательностн. Для линии Z = Z _L— Z _M — сопротивле­ние прямой последовательности; Z ₂= Z _L— Z _M — сопротив­ление обратной последовательности; Z ₀= Z _l+2Z_M — со­противление нулевой последовательности, причем Z _l = Z ₂≠ Z ₀

Взаимная независимость уравнений (11.20) свидетель­ствует о принципиальной возможности независимого рас­чета режимов, составленных из сопротивлений прямой, обратной и нулевой последовательностей. Такая возмож­ность и определяет целесообразность расчетов несиммет­ричных режимов в системе координат симметричных со­ставляющих при равенстве фазных сопротивлений схемы.

При найденных фазных токах и напряжениях, характе­ризующих несимметричный режим, активные мощности в любой (-й ветви схемы определяются общим уравнением

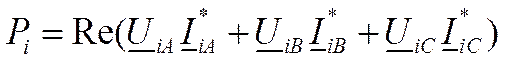
Эти же мощности могут быть найдены и по результатам расчета в системе координат симметричных составляюших. Можно показать, что

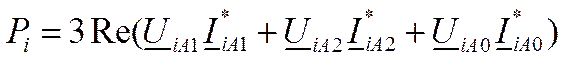
Выше рассмотрены уравнения закона Ома для участка грехфазной линии. Все приведенные выше рассуждения справедливы для уравнений установившегося режима сложной трехфазной сети, в которой, например, имеются несимметричные нагрузки. Для такой сети можно записать аналогично (11.20) уравнения узловых напряжений неза­висимо для каждой последовательности при напряжении базисного узла, равном нулю, в следующем виде:

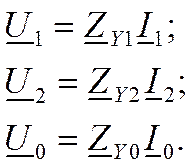
где U ₁, U ₂, U _o, I ₁, I ₂, I _o - векторы узловых напряжений и узловых токов соответственно прямой, обратной и нуле­вой последовательностей; Z _y1, Z _y2, Z _y0 — матрицы собст­венных и взаимных сопротивлений прямой, обратной и ну­левой последовательностей.

Аналогично можно записать линейные уравнения уста­новившегося режима сложной трехфазной сети в других формах (с матрицей узловых проводимостей Y_y либо при U_б ≠ 0 в виде трех независимых систем узловых урав­нений для каждой из последовательностей. Основное пре­имущество метода симметричных составляющих при рас­четах на ЭВМ заключается в возможности при равенстве взаимных междуфазных активных сопротивлений и сопро­тивлений самоиндукции независимо решать систему урав­нений для каждой из последовательностей. Это дает воз­можность в 3 раза понизить порядок решаемой системы, т.е. уменьшить время расчета и требуемую память.

6-4. Эксплуатация генераторов.

-это управление режимом ген-ра или поддержание магнитного поля между статором и ротором.

Изменение результирующего поля компенсируется изменением тока возбуждения в широких пределах в зависимости от его режима

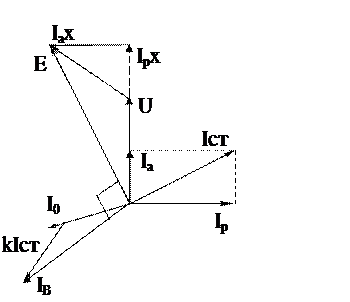
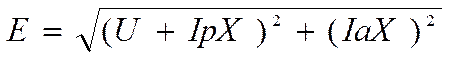
Магнитный поток х.х. создается током возбуждения Io. Магнитный поток, компенсирующий реакцию якоря, соответствует составляющей тока возбуждения kI ст. Рез-ий магн-ый поток соотв-ет полному току возб-ия Iв.

Х-индуктивность рассеяния генератора.

Используя I₀= β E можно в определенном масштабе совместить токи возб-ия с пропорциональными им параметрами режима генератора.

Изменение напряжения ген-ра может быть сл-ем изм-я режима др-х ген-ов. Предельно допустимый реактивный ток опред-ся по усл нагрева обм-ки возб-я. Автоматика регулир-я возб-я производит необходимые изм-я Iв по факту изм-я напр-я на вводах ген-ра. Сущ-ет два режима ген-ра перевозб-я – отдачи в сеть мощности и недовозбуждения – потребл-е из сети реакт м-ти. Режим недовозб-я ограничен нагревом крайних пакетов железа статора.

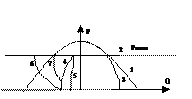
1-линия ограничения тока статора 3-огр-ие по току возб-ия 4, 5-ограничивают допустим.потреб. реакт-ый мощность по усл. нагрева крайних пакетов железа статора. 6, 7 ограничение по условию стат-ой уст-ти

Для обеспечения устойчивости распределение реакт-ой м-ти м/у паралл раб-ми ген-ми АРВ должен иметь стат-ю хар-ку при которой созданием реактивной мощности сниж-ся напр-ие на выводах ген-ра.

Системы возбуждения генератора

До 100 Мвт-эл. маш. Возбуждение, свыше-пост. Тока

1% от мощ-ти ген-ра – это мощь возбудителя

Системы охлаждения генератора

Удельные потери: обм.возб-ия- 150-250Вт/кг, обм.статора- 70-100, торцевые пакеты статора- 20-35, нажимные плиты- 15-30

Система водородного охлаждения ТВ, ТВФ, ТВГ. Сам водород охл-ся газоохладительной водойводород взрывоопасен, если его в воздухе 5-81, 5%

Для осушки водорода применяют фильтры сорбционного типа или холо

дильники. 200Ком/см – проводимость дистиллята для водородно-водяного охл-ия (для обмотки возб-ия).Трансформаторное масло прим.для охл-ия обмотки стали статора