
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы математической статистики в психоаого-педагогическом иссаедовании
|
|
Применение математики к другим наукам имеет смысл только в единении с глубокой теорией конкретного явления. Об этом важно помнить, чтобы не сбиваться на простую игру в формулы, за которой не стоит никакого реального содержания.
Академик Ю. А. Митрополъский
Теоретические методы исследования в психологии и педагогике дают возможность раскрыть качественные характеристики изучаемых явлений. Эти характеристики будут полнее и глубже, если накопленный эмпирический материал подвергнуть количественной обработке. Однако проблема количественных измерений в рамках психолого-педагогических исследований очень сложна. Эта сложность заключается прежде всего в субъективно-причинном многообразии педагогической деятельности и ее результатов, в самом объекте измерения, находящемся в состоянии непрерывного движения и изменения. Вместе с тем введение в исследование количественных показателей стало сегодня необходимым и обязательным компонентом получения объективных данных о результатах педагогического труда. Как правило, эти данные могут быть получены путем прямого или опосредованного измерения различных составляющих педагогического процесса либо посредством количественной оценки соответствующих параметров адекватно построенной математической модели педагогического процесса. С этой целью при исследовании проблем психологии и педагогики применяются методы математической статистики. С их помощью решаются различные задачи: обработка фактического материала, получение новых, дополнительных данных, обоснование научной организации исследования и др
Основные понятия математической статистики
Исключительно важную роль в анализе многих психолого-педагогических явлений играют средние величины, представляющие собой обобщенную характеристику качественно однородной совокупности по определенному количественному признаку. Нельзя, например, вычислить среднюю специальность или среднюю национальность студентов вуза, так как специальность и национальность — качественно разнородные явления. Зато можно и нужно определить среднюю количественную характеристику их успеваемости (средний балл), эффективности методических систем и приемов и т. д.
В психолого-педагогических исследованиях обычно применяются различные виды средних величин: средняя арифметическая, средняя геометрическая, медиана, мода и др. Наиболее распространены средняя арифметическая, медиана и мода.
Средняя арифметическая применяется в тех случаях, когда между определяющим свойством и данным признаком имеется прямо пропорциональная зависимость (например, при улучшении показателей работы учебной группы улучшаются показатели работы каждого ее члена).
Средняя арифметическая представляет собой частное от деления суммы величин на их число и вычисляется по формуле
где X — средняя арифметическая; Хь Х2, Х3... Хы — результаты отдельных наблюдений (приемов, действий), N — количество наблюдений (приемов, действий), Σ — сумма результатов всех наблюдений (приемов, действий).
Медианой (Ме) называется мера среднего положения, характеризующая значение признака на упорядоченной (построенной по признаку возрастания или убывания) шкале, которое соответствует середине исследуемой совокупности. Медиана может быть определена для порядковых и количественных признаков. Место расположения этого значения определяется по формуле
Л. N + 1
Место медианы =
 Например, по результатам исследования установлено, что:
Например, по результатам исследования установлено, что:
на «отлично» учатся 5 человек из участвующих в эксперименте;
на «хорошо» — 18 человек;
на «удовлетворительно» — 22 человека;
на «неудовлетворительно» — 6 человек.
Так как всего в эксперименте принимало участие N = 54 человека, то середина выборки равна 0, 5 х N= 27 человек. Отсюда делается вывод, что больше половины обучающихся учатся ниже оценки «хорошо», т. е. медиана больше «удовлетворительно», но меньше «хорошо» (рис. 6.1
Мода (Мо) — наиболее часто встречающееся типичное значение признака среди других значений. Она соответствует классу с максимальной частотой. Этот класс называется модальным значением.
Например, если ответы на вопрос анкеты «Укажите степень владения иностранным языком» распределились таким образом:
1 — владею свободно — 25;
2 — владею в степени, достаточной для общения — 54;
3 — владею, но испытываю трудности при общении — 253;
4 — понимаю с трудом — 173;
5 — не владею — 28,
то очевидно, что наиболее типичным значением здесь является «Владею, но испытываю трудности при общении», которое и будет модальным. Таким образом, мода равна 253.
Важное значение при использовании в психолого-педагогическом исследовании математических методов уделяется расчету дисперсии и среднеквадратических (стандартных) отклонений.
Дисперсия равна среднему квадрату отклонений значения исследуемой переменной от среднего значения. Она выступает как одна из характеристик индивидуальных результатов разброса значений исследуемой переменной (например, оценок учащихся) вокруг среднего значения. Вычисление дисперсии осуществляется путем определения:
♦ отклонения от среднего значения;
♦ квадрата указанного отклонения;
♦ суммы квадратов отклонения и среднего значения квадрата отклонения (табл. 6.1
Значение дисперсии используется в различных статистических расчетах, но не имеет непосредственного наблюдаемого характера. Величиной, непосредственно связанной с содержанием наблюдаемой переменной, является среднее квадратическое отклонение.

 Среднее квадратическое отклонение подтверждает типичность и показательность средней арифметической, отражает меру колебания численных значений признаков, из которых выводится средняя величина. Оно равно корню квадратному из дисперсии и определяется по формуле
Среднее квадратическое отклонение подтверждает типичность и показательность средней арифметической, отражает меру колебания численных значений признаков, из которых выводится средняя величина. Оно равно корню квадратному из дисперсии и определяется по формуле
где а — средняя квадратическая. При малом числе наблюдения (действий) — менее 100 — в значении формулы следует ставить не N, аN-1.
Средняя арифметическая и средняя квадратическая являются основными характеристиками полученных результатов в ходе исследования. Они позволяют обобщить данные, сравнить их, установить преимущества одной психолого-педагогической системы (программы) над другой.
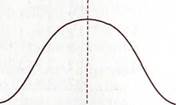
Среднее квадратическое (стандартное) отклонение широко применяется как мера разброса для различных характеристик. На рис. 6.2 приведен пример распределения частот значений двух переменных с одинаковыми средними, но различным разбросом.

 Значение переменной
Значение переменной
Рис. 6.2. Кривая нормального распределения вероятности случайной величины (закон Гаусса)
Оценивая результаты исследования, важно определить рассеивание случайной величины около среднего значения. Это рассеивание описывается с помощью закона Гауса (закона нормального распределения вероятности случайной величины). Суть закона заключается в том, что при измерении некоторого признака в данной совокупности элементов всегда имеют место отклонения в обе стороны от нормы вследствие множества неконтролируемых причин, при этом чем больше отклонения, тем реже они встречаются.
При дальнейшей обработке данных могут быть выявлены: коэффициент вариации (устойчивости) исследуемого явления, представляющий собой процентное отношение среднеквадратического отклонения к средней арифметической; мера косости, показывающая, в какую сторону направлено преимущественное число отклонений; мера крутости, которая показывает степень скопления значений случайной величины около среднего и др. Все 

 Среднее квадратическое отклонение подтверждает типичность и показательность средней арифметической, отражает меру колебания численных значений признаков, из которых выводится средняя величина. Оно равно корню квадратному из дисперсии и определяется по формуле
Среднее квадратическое отклонение подтверждает типичность и показательность средней арифметической, отражает меру колебания численных значений признаков, из которых выводится средняя величина. Оно равно корню квадратному из дисперсии и определяется по формуле
где а — средняя квадратическая. При малом числе наблюдения (действий) — менее 100 — в значении формулы следует ставить не N, аN-1.
Средняя арифметическая и средняя квадратическая являются основными характеристиками полученных результатов в ходе исследования. Они позволяют обобщить данные, сравнить их, установить преимущества одной психолого-педагогической системы (программы) над другой.
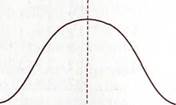
Среднее квадратическое (стандартное) отклонение широко применяется как мера разброса для различных характеристик. На рис. 6.2 приведен пример распределения частот значений двух переменных с одинаковыми средними, но различным разбросом.

 Значение переменной
Значение переменной
Рис. 6.2. Кривая нормального распределения вероятности случайной величины (закон Гаусса)
Оценивая результаты исследования, важно определить рассеивание случайной величины около среднего значения. Это рассеивание описывается с помощью закона Гауса (закона нормального распределения вероятности случайной величины). Суть закона заключается в том, что при измерении некоторого признака в данной совокупности элементов всегда имеют место отклонения в обе стороны от нормы вследствие множества неконтролируемых причин, при этом чем больше отклонения, тем реже они встречаются.
При дальнейшей обработке данных могут быть выявлены: коэффициент вариации (устойчивости) исследуемого явления, представляющий собой процентное отношение среднеквадратического отклонения к средней арифметической; мера косости, показывающая, в какую сторону направлено преимущественное число отклонений; мера крутости, которая показывает степень скопления значений случайной величины около среднего и др. Все Таким образом, коэффициент корреляции Пирсона для выбранного примера равен 0, 32, т. е. зависимость между семейным положением студентов и фактами исключения из университета незначительная.
Значение коэффициента Спирмена изменяется в пределах от - 1 до +1. В первом случае между анализируемыми переменными существует однозначная, но противоположено направленная связь (с увеличением значений одной уменьшается значения другой). Во втором с ростом значений одной переменной пропорционально возрастает значение второй переменной. Если величина Д. равна нулю или имеет значение, близкое к нему, то значимая связь между переменными отсутствует.
Статистическая проверка научной гипотезы. Доказательство статистической достоверности экспериментального влияния существенно отличается от доказательства в математике и формальной логике, где выводы носят более универсальный характер: статистические доказательства не являются столь строгими и окончательными — в них всегда допускается риск ошибиться в выводах, и потому
статистическими методами не доказывается окончательно правомерность того или иного вывода, а показывается мера правдоподобности принятия той или иной гипотезы.
Педагогическая гипотеза (научное предположение о преимуществе того или иного метода и т. п.) в процессе статистического анализа переводится на язык статистической науки и заново формулируется, по меньшей мере, в виде двух статистических гипотез. Первая (основная) называется нулевой гипотезой (Яо), в которой исследователь говорит о своей исходной позиции. Он априори как бы декларирует, что новый метод (предполагаемый им, его коллегами или оппонентами) не обладает какими-либо преимуществами, и потому с самого начала исследователь психологически готов занять честную научную позицию: различия между новым и старым методами объявляются равными нулю. В другой, альтернативной гипотезе (Н{) делается предположение о преимуществе нового метода. Иногда выдвигается несколько альтернативных гипотез с соответствующими обозначениями.
Например, гипотеза о преимуществе старого метода обозначается как (Н2). Альтернативные гипотезы принимаются тогда и только тогда, когда опровергается нулевая гипотеза. Это бывает в случаях, когда различия, скажем, в средних арифметических экспериментальной и контрольной групп настолько значимы (статистически достоверны), что риск ошибки отвергнуть нулевую гипотезу и принять альтернативную не превышает одного из трех принятых уровней значимости статистического вывода:
♦ первый уровень — 5 % (в научных текстах пишут иногда р = 5 % или а < 0, 05, если представлено в долях), где допускается риск
ошибки в выводе в пяти случаях из ста теоретически возможных таких же экспериментов при строго случайном отборе испытуемых для каждого эксперимента;
♦ второй уровень — 1 %, т. е. соответственно допускается риск ошибиться только в одном случае из ста (а < 0, 01, при тех же требованиях);
♦ третий уровень — 0, 1 %, т. е. допускается риск ошибиться только
в одном случае из тысячи (а < 0, 001).
Последний уровень значимости предъявляет очень высокие требования к обоснованию достоверности результатов эксперимента и потому редко используется.

 При сравнении средних арифметических экспериментальной и контрольной групп важно определить, какая средняя не только больше, но и насколько больше. Чем меньше разница между ними, тем более приемлемой окажется нулевая гипотеза об отсутствии статистически значимых (достоверных) различий. В отличие от мышления на уровне обыденного сознания, склонного воспринимать полученную в результате опыта разность средних как факт и основание для вывода, педагог-исследователь, знакомый с логикой статистического вывода, не будет торопиться в таких случаях. Он, скорее всего, сделает предположение о случайности различий, выдвинет нулевую гипотезу об отсутствии достоверных различий в результатах экспериментальной и контрольной групп и лишь после опровержения нулевой гипотезы примет альтернативную.
При сравнении средних арифметических экспериментальной и контрольной групп важно определить, какая средняя не только больше, но и насколько больше. Чем меньше разница между ними, тем более приемлемой окажется нулевая гипотеза об отсутствии статистически значимых (достоверных) различий. В отличие от мышления на уровне обыденного сознания, склонного воспринимать полученную в результате опыта разность средних как факт и основание для вывода, педагог-исследователь, знакомый с логикой статистического вывода, не будет торопиться в таких случаях. Он, скорее всего, сделает предположение о случайности различий, выдвинет нулевую гипотезу об отсутствии достоверных различий в результатах экспериментальной и контрольной групп и лишь после опровержения нулевой гипотезы примет альтернативную.
Таким образом, вопрос о различиях в рамках научного мышления переводится в другую плоскость. Дело не только в различиях (они почти всегда есть), а в величине этих различий и отсюда — в определении разницы и границы, после которого можно сказать: да, различия неслучайны, они статистически достоверны, а значит, испытуемые этих двух групп принадлежат после эксперимента уже не к одной (как раньше), а к двум различным генеральным совокупностям, и уровень подготовленности учащихся, потенциально принадлежащих этим совокупностям, будет существенно отличаться. Для того чтобы показать границы этих различий, используются так называемые оценки генеральных параметров.
Рассмотрим на конкретном примере (табл. 6.6), как с помощью математической статистики можно опровергнуть или подтвердить нулевую гипотезу.
Допустим, необходимо определить, зависит ли эффективность групповой деятельности студентов от уровня развития межличностных отношений в их учебной группе. В качестве нулевой гипотезы выдвигается предположение, что такой зависимости не существует, а в качестве альтернативной — зависимость существует. Для этих целей сравниваются результаты эффективности деятельности в двух группах, одна из которых в этом случае выступает в качестве экспериментальной, а вторая — контрольной. Чтобы определить, является ли разность между средними значениями показателей эффективности в первой и во второй группах существенной (значимой), необходимо вычислить статистическую достоверность этой разницы. Для
Многомерные методы анализа данных. Анализ взаимосвязи между большим количеством переменных осуществляется путем использования многомерных методов статистической обработки. Цель применения подобных методов — обнаружить скрытые закономерности, выделить наиболее существенные взаимосвязи между переменными. Примерами таких многомерных статистических методов являются:
факторный анализ; кластерный анализ; дисперсионный анализ; регрессионный анализ; латентно-структурный анализ; многомерное шкалирование и др.
Факторный анализ заключается в выявлении и интерпретации факторов. Фактор — обобщенная переменная, которая позволяет свернуть часть информации, т. е. представить ее в удобообозримом виде. Например, факторная теория личности выделяет ряд обобщенных характеристик поведения, которые в данном случае называются чертами личности.
Кластерный анализ позволяет выделить ведущий признак и иерархию взаимосвязей признаков.
Дисперсионный анализ — статистический метод, используемый для изучения одной или нескольких одновременно действующих и независимых переменных на изменчивость наблюдаемого признака. Его особенность состоит в том, что наблюдаемый признак может быть только количественным, в то же время объясняющие признаки могут быть как количественными, так и качественными.
Регрессионный анализ позволяет выявить количественную (численную) зависимость среднего значения изменений результативного признака (объясняемой) от изменений одного или нескольких признаков (объясняющих переменных). Как правило, данный вид анализа применяется в том случае, когда требуется выяснить, насколько изменяется средняя величина одного признака при изменении на единицу другого признака.
Латентно-структурный анализ представляет собой совокупность аналитико-статистических процедур выявления скрытых переменных (признаков), а также внутренней структуры связей между ними
Он дает возможность исследовать проявления сложных взаимосвязей непосредственно ненаблюдаемых характеристик социально-психологических и педагогических феноменов. Латентный анализ может стать основой для моделирования указанных взаимосвязей.
Многомерное шкалирование обеспечивает наглядную оценку сходства или различия между некоторыми объектами, описываемыми большим количеством разнообразных переменных. Эти различия представляются в виде расстояния между оцениваемыми объектами в многомерном пространстве.
Статистическая обработка результатов психолого-педагогического исследования
В любом исследовании всегда важно обеспечить массовость и представительность (репрезентативность) объектов изучения. Для решения этого вопроса обычно прибегают к математическим методам расчета минимальной величины подлежащих исследованию объектов (групп респондентов), чтобы на этом основании можно было сделать объективные выводы.
По степени полноты охвата первичных единиц статистика делит исследования на сплошные, когда изучаются все единицы изучаемого явления, и выборочные, если изучению подвергается только часть интересующих явлений, взятая по какому-либо признаку. Исследователю не всегда представляется возможность изучить всю совокупность явлений, хотя к этому постоянно следует стремиться, но, с другой стороны, сплошное исследование часто просто не требуется, так как выводы будут достаточно точными после изучения определенной части первичных единиц.
Теоретической основой выборочного способа исследования выступает теория вероятностей и закон больших чисел. Чтобы исследование располагало достаточным количеством фактов, наблюдений, используют таблицу достаточно больших чисел. От исследователя в данном случае требуется установление величины вероятности и величины допускаемой ошибки. Пусть, например, допускаемая ошибка в выводах, которые должны быть сделаны в результате наблюдений, по сравнению с теоретическими предположениями, не должна превышать 0, 05 как в положительную, так и в отрицательную стороны (иначе говоря, мы можем ошибиться не более чем в 5 случаях из 100). Тогда по таблице достаточно больших чисел (табл. 6.7)' находим, что правильное заключение может быть сделано в 9 случаях из 10 тогда, когда число единиц наблюдения будет не менее 270, в 99 случаях из 100 — при наличии не менее 663 единиц и т. д. Значит, с увеличением точности и вероятности, с которой мы предполагаем сделать выводы, величина требуемой выборки возрастает. Однако в психолого-педагогическом исследовании она не должна быть чрезмерно большой. Как правило, для основательных выводов вполне достаточно 300-500 выбранных для наблюдения единиц.
Данный способ определения величины выборки является наиболее простым. Математическая статистика располагает и более сложными методами вычисления требуемых выборочных совокупностей, которые подробно освещены в специальной литературе.
Однако соблюдение требований массовости еще не обеспечивает надежности выводов. Они будут достоверны тогда, когда единицы, выбранные для наблюдения (бесед, эксперимента и т. д.), будут достаточно представительными для изучаемого класса явлений.
Таблица 6.7
Краткая таблица достаточно больших чисел
| Допустимая ошибка | Величина вероятности | |||||
| 0, 85 | 0, 90 | 0, 95 | 0, 99 | 0, 995 | 0, 999 | |
| 10, 05 | ||||||
| 10, 04 | ||||||
| 10, 03 | ||||||
| 10, 02 | ||||||
| 10, 01 |
Репрезентативность единиц наблюдения обеспечивается прежде всего их случайным выбором с помощью таблиц случайных чисел. Положим, для проведения массового эксперимента требуется определить 20 учебных групп из имеющихся 200. Для этого составляется нумерованный список всех групп. Затем из таблицы случайных 

 чисел выписываются 20 номеров, начиная с какого-либо числа, через определенный интервал. Эти 20 случайных чисел определяют те группы, которые нужны исследователю. Случайный выбор объектов из общей (генеральной) совокупности дает основание утверждать, что полученные при исследовании выборочной совокупности единиц результаты не будут резко отличаться от тех, которые имелись бы в случае исследования всей совокупности единиц.
чисел выписываются 20 номеров, начиная с какого-либо числа, через определенный интервал. Эти 20 случайных чисел определяют те группы, которые нужны исследователю. Случайный выбор объектов из общей (генеральной) совокупности дает основание утверждать, что полученные при исследовании выборочной совокупности единиц результаты не будут резко отличаться от тех, которые имелись бы в случае исследования всей совокупности единиц.
В практике психолого-педагогических исследований применяются не только простые случайные отборы, но и более сложные методы отбора: расслоенный случайный отбор, многоступенчатый отбор и др.
Математические и статистические методы исследования являются также средствами получения нового фактического материала. С этой целью используются приемы шаблонирования, повышающие информативную емкость анкетного опроса и приемы шкалирования, дающие возможность более точно оценивать действия как исследователя, так и исследуемых.
Шкалы возникли из-за необходимости объективно и точно диагностировать и измерять интенсивность определенных психолого-педагогических явлений. Шкалирование дает возможность упорядочить, количественно оценить, определить низшую и высшую ступени исследуемого явления.
Так, при исследовании познавательных интересов студентов можно установить их границы: очень большой интерес — очень слабый интерес. Между этими границами ввести ряд ступеней, создающих шкалу познавательных интересов: очень большой интерес (1); большой интерес (2); средний (3); слабый (4); очень слабый (5).
В психолого-педагогических исследованиях используются шкалы разных видов, например: