Двойственность в ЛП.

Каждой задаче ЛП с любым типом ограничений можно поставить в соответствие другую задачу, которая называется двойственной по отношению к первой. Совместное рассмотрение таких пар задач позволяет исследовать влияние изменения переменных системы на значение целевой функции, проводить экономический анализ результатов расчета.

Правила построения двойственной задачи:

1. Если прямая задача была задачей максимума, то двойственная будет задачей минимума, и на оборот;

2. Число переменных двойственной задачи равно числу ограничений прямой, и наоборот;

3. Коэффициенты целевой функции прямой задачи становятся свободными членами ограничений двойственной задачи;

4. Свободные члены ограничений прямой задачи становятся коэффициентами целевой функции двойственной задачи;

5. Матрица ограничений двойственной задачи получается транспонированием матрицы ограничений прямой, и наоборот;

6. Взаимно однозначное соответствие между переменными исходной задачи и ограничениями двойственной удовлетворяет следующему положению:

А) если J-ая переменная неотрицательна в прямой задаче, то J-ое ограничение в двойственной задаче это неравенство типа 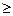; переменным не имеющих ограничений в знаке соответствует ограничение равенство;

Б) если I-ое ограничение прямой задачи неравенство типа 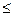, то

I-ая переменная двойственной задачи неотрицательна; ограничениям равенствам отвечает переменная без ограничений в знаке.

Пример: Построить задачу, двойственную к данной:

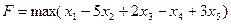
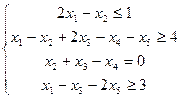
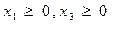
Перепишем задачу изменяя ограничения типа 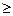на ограничения типа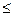 . Получим задачу:

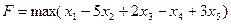
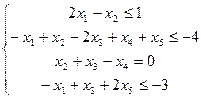
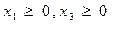
Двойственная задача имеет вид:

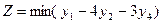
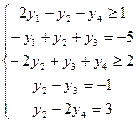
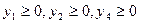
Вопрос для самоподготовки

1. Когда используется метод искусственного базиса при определении опорного плана?

2. Как организуется симплекс-таблица при решении задачи ЛП методом искусственного базиса?

3. Как определяется, что задача не имеет опорных планов?

4. Двойственная задача - это модель прикладной задачи или ее превращения?

5. Как определить количество переменных у двойной задачи, если известна прямая задача?

6. Как определить знаки двойных переменных?

ЛЕКЦИЯ 6.