
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание к лабораторной работе. 3.1.Выбрать значения коэффициентов из таблицы для функции в соответствии с вариантом.
|
|
3.1.Выбрать значения коэффициентов из таблицы для функции 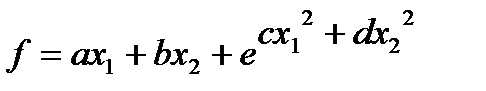 в соответствии с вариантом.
в соответствии с вариантом.
| Вариант | a | b | c | d |
| 1.1 | 0.01 | 0.11 | ||
| -1.3 | 0.04 | 0.12 | ||
| -1.2 | 0.02 | 0.13 | ||
| -1.1 | 0.16 | 0.14 | ||
| -1 | 0.25 | 0.15 | ||
| -0.9 | 0.35 | 0.16 | ||
| -0.8 | 0.49 | 0.17 | ||
| 1.96 | 0.12 | |||
| 0.1 | 1.99 | 0.13 | ||
| 0.2 | 2.56 | 0.14 | ||
| 0.3 | 2.89 | 0.15 | ||
| 0.4 | 3.24 | 0.16 | ||
| 0.5 | 3.81 | 0.27 | ||
| -0.1 | 1.69 | 0.24 | ||
| 1.96 | 0.25 | |||
| 0.1 | 1.99 | 0.26 | ||
| 0.2 | 2.56 | 0.27 | ||
| 0.3 | 2.89 | 0.28 | ||
| 0.4 | 3.24 | 0.29 | ||
| 0.5 | 3.81 | 0.3 | ||
| -1.2 | 1.96 | 0.17 | ||
| -1.1 | 1.99 | 0.12 | ||
| -1 | 2.56 | 0.13 | ||
| -0.9 | 2.89 | 0.14 | ||
| -0.8 | 3.24 | 0.15 |
3.2. Решить задачу оптимизации методом градиентов для трех вариантов исходных данных.
3.3. Выполнить анализ полученных решений.
3.4. Оформить отчет по лабораторной работе.
Контрольные вопросы
1. Характеристика градиента функции.
2. Алгоритм нахождения минимума функции.
3. Исходные данные.
4. Выбор рабочего шага.
5. Оценка точности поиска.
Приложение
program grad;
const max=1000; {максимальное количество шагов}
a=1.0;
b=-1.4;
c=0.01;
d=0.11;
label 10;
var k: integer;
h, h1, f1, f2, eps: real;
x, y: array [1..max+1] of real;
//Исходная функция
function f(p1, p2: real): real;
begin
f: =a*p1+b*p2+exp(c*sqr(p1)+d*sqr(p2))
end;
//Частная производная по первой переменной
function px(p: integer): real;
begin
px: =a+2*c*x[p]*exp(c*sqr(x[p])+d*sqr(y[p]))
end;
//Частная производная по второй переменной
function py(p: integer): real;
begin
py: =b+2*d*y[p]*exp(c*sqr(x[p])+d*sqr(y[p]))
end;
begin
cls;
writeln ('Исходные данные');
writeln;
writeln('Задайте начальные приближения');
write('x1='); readln(x[1]);
write('x2='); readln(y[1]);
write ('Задайте точность eps='); readln(eps);
write ('Задайте начальный шаг h='); readln(h1);
k: =1;
repeat
h: =h1; inc(k);
repeat
x[k]: =x[k-1]-h*px(k-1);
y[k]: =y[k-1]-h*py(k-1);
f1: =f(x[k-1], y[k-1]);
f2: =f(x[k], y[k]);
h: =h/2;
until f2< f1;
if k> max then
begin
writeln ('Превышено максимальное количество шагов, выполнено', max, ' шагов');
goto 10;
end;
//Оценка точности по минимальному значению модуля градиента
until sqrt(sqr(px(k))+sqr(py(k)))< eps;
writeln;
writeln ('Результаты решения');
writeln;
writeln ('Оптимальные значения переменных');
writeln('x1= ', x[k]: 2: 8);
writeln('x2= ', y[k]: 2: 8);
writeln ('Минимальное значение целевой функции');
writeln('f= ', f2: 2: 8);
writeln ('Количество выполненных шагов');
writeln ('k=', k-1);
writeln ('Текущая длина шага');
writeln ('h=', h*2);
10: end.