Тестіге жауап

Файл ТЕСТ по ЭММ каз.doc

Оқ у жылына арналғ ан «ЭММ» пә нінен тестілік сұ рақ атр

Семестр БУА -31тобы

Тестіге жауап

Реттік№	Кү рделілік дең гейі	Сұ рақ	Бө лім, тақ ырып	Жауап A) (дұ рыс)	Жауап B)	Жауап C)	Жауап D)	Жауап E)
1.		Модель ол		Тү пнұ сқ аның негізгі қ асиеттерін қ айталайтын кө шірме ү лгі	Тү пнұ сқ а	Тү пнұ сқ аның негізгі қ асиеттерін қ айталамайтын кө шірме ү лгі	Кө шірменің негізгі қ асиеттерін қ айталамайтын ү лгі	Дерек
2.		ЭММ дегеніміз		Экономикалық проблеманы зерттейтін математикалық модель	Математикалық проблеманы зерттейтін экономикалық модель	Дифференциалдық тең деу	Деректердің кестесі	Деректердің қ асиеті
3.		ЭММ - ге жатпайтын модель		Стохастикалық модель	Детерминантты модель	Динамикалық модель	Статикалық модель	Физикалық модель
4.		Айнымалы дегеніміз		Мә ні ө згеріп отыратын шама	Мә ні ө згермейтін шама	Константа	Шектеу	Формула
5.		Базистік айнымалы ол-		Шешімдерді сипаттайтын айнымалы	Негізгі айнымалы	Қ осымша айнымалы	Шешімдерді сипаттамайтын айнымалы	Формула
6.		Симплекстік тә сіл … шешуге қ олданылады		Сызық тық программалау есебін	Сызық тық емес программалық есепті	Динамикалық есепті	Дифференциалдық есепті	Интегралдық есепті
7.		СПЕ канондық тү рі дегеніміз		Шарттардың тең деумен берілуі	Шарттардың тең сіздікпен берілуі	Шарттардың болмауы	Шарттардың теріс болуы	Геометриялық сипатталуы
8.		СПЕ стандарттық тү рі дегеніміз		Шарттардың тең сіздікпен берілуі	Шарттардың тең деумен берілуі	Шарттардың болмауы	Шарттардың теріс болуы	Геометриялық сипатталуы
9.		Еркін айнымалы ол …… айнымалы		Шешімдерді табуғ а кө мектесетін	Шешімдерді сипаттайтын	Қ осымша	Мә ні теріс болатын	Сан
10.		СПЕ стандарттық кү йден канондық кү йге …….айнымалылар арқ ылы жеткізіледі		Қ осымша	Кө мекші	Еркін	Бірлік	Сандық
11.		Симплекс ……. білдіреді		Дө ң ес кө пбұ рышты	Ойыс кө пбұ рышты	Кесіндіні	Тү зуді	Санды
12.		Техникалық экономикалық коэффициент		Ресурстардың ө німнің бірлігіне кететін шығ ынын сипаттайды	ө німнің бірлігінен келетін пайданы сипаттайды	Икемділік	Байланысты сипаттайды	ө рнекті сипатайды
13.		Сызық тық программалау есебі (СПЕ) …..ү йретеді		Қ олдағ ы бар ресурсты ұ тымды пайдалануды	Қ олдағ ы жоқ ресурсты ұ тымды пайдалануды	График жасауды	Программа қ ұ руды	Программа қ ұ рмауды
14.		Тиімділік критериі ол		Қ ол жеткізілуге тиісті сандық шама	Тең деудің шешімінің болуы	Ресурстардың керекті мө лшері	Шексіз шама	Коэффициент
15.		Абстрактілік модель		Арнайы таң балар арқ ылы сипатталатын кө шірме ү лгі	Физикалық қ асиеттері бар кө шірме ү лгі	Арнайы таң балар арқ ылы сипатталатын тү пнұ сқ а	Арнайы таң балар арқ ылы сипатталмайтын кө шірме ү лгі	Муляж
16.		Физикалық модель		Тү пнұ сқ аның тү рін тү сін тұ рпатын қ айталайтын кө шірме ү лгі	Арнайы таң балар арқ ылы сипатталатын кө шірме ү лгі	Объектінің тү пнұ сқ асы	Зерттелмейтін кө шірме ү лгі	Формула
17.		Мақ сатты функция дегеніміз		Тиімділік критериінің математикалық тү рде жазылуы	Есептің шарттары	Дифференциалды тең деу	Интегралды функция	Дискретті функция
18.		СПЕ.Симплекс тә сіліндегі тиімділік белгісі		Индексті жолда оң (теріс) элементтердің болмауы	Шешуші элементтің теріс болуы	Шешуші элементтің оң болуы	Шешуші бағ ананың мә ндерінің 0 ге тең болуы	Элементтердің 1-ге тең болуы
19.		СПЕ. М- тә сілін қ олдану ү шін шарттарда …..таң басы болуы керек		³	£	¹	=	<
20.		ТТасымал есебі деп ….. атайды		Жү к тасудағ ы кететін шығ ынның min мө лшерін есептеуді	Жү к тасудағ ы кететін шығ ынның max-ды мө лшерін есептеуді	Жү кті тасудағ ы кететін шығ ынды болдырмауды	Жү кті тасудағ ы кететін шығ ынның теріс мә нге ие болуды	Жү кті тасудағ ы кететін шығ ынды болдыруды
21.		ТЕ. m-		Жабдық таушының саны	Тұ тынушы саны	Тасылатын жү ктің мө лшері	Тариф	Жолдар саны
22.		ТЕ. n-		Тұ тынушы саны	Жабдық таушының саны	Тасылатын жү ктің мө лшері	Тариф	Жолдар саны
23.		ТЕ. Аі-		і-ші пункттегі жү ктің мө лшері	j-ші пункттегі жү ктің мө лшері	Жабдық таушының саны	Тариф	Жолдар саны
24.		ТЕ. Bj-		j-ші пункттегі тұ тынатын жү ктің мө лшері	i-ші пункттегі тұ тынатын жү ктің мө лшері	Тасылатын жү ктің мө лшері	Тариф	Жолдар саны
25.		TE. Cij-		Тариф	Тасылатын жү ктің мө лшері	j-ші пункттегі тұ тынатын жү ктің мө лшері	Жабдық таушының саны	Жолдар саны
26.		TE. Хij-		Тасылатын жү ктің мө лшері	Тариф	j-ші пункттегі тұ тынатын жү ктің мө лшері	Жабдық таушының саны	Жолдар саны
27.		ТЕ. å Аі=å Вj нені білдіреді		Жабық модельді	Ашық модельді	ТЕ шешілмейтіндігін	Тұ тынушынң жетіспейтіндігін	Есептің шығ арылмайтынын
28.		ТЕ. å Аі¹ å Вj нені білдіреді		Ашық модельді	Жабық модельді	ТЕ шешілетіндігін	Тұ тынушынң жетіспейтіндігін	Характеристиканың оң екенін
29.		ТЕ. å Xij=Bj нені білдіреді		Тұ тынушы сұ ранысының толық тай ө телуін	Жабдық таушыдан жү ктің толық тай ә кетілуін	Ашық модельді	Жабық модельді	Есептің шешілмейтінін
30.		ТЕ. å Xij=Аi нені білдіреді		Жабдық таушыдан жү ктің толық тай ә кетілуін	Тұ тынушы сұ ранысының толық тай ө телуін	Ашық модельді	Жабық модельді	Есептің шешілмейтінін
31.		ТЕ. Хij ³ 0 нені білдіреді		Кері тасымалдың болмауын	Тура тасымалдың болмауын	Тұ тынушы сұ ранысының толық тай ө телуін	ТЕ шешілетіндігін	Есептің шешілмейтінін
32.		ТЕ. Тиімді маршрут саны неге тең		n+m-1	n-m-1	n+m+1	n-m+1	n+m
33.		TE. Потенциалдарды анық тау формуласы		Cij=ui+vj	Cij=ui-vj	Cij=ui*vj	Cij=ui/vj	Cij=ui+vj+1
34.		TE. Харак-теристикаларды анық тау формуласы		Wij=cij-(ui+vj)	Wij=cij-(ui-vj)	Wij= (ui+vj)	Wij=cij-ui	Wij=cij
35.		ТЕ. Жақ сарту жұ мысы ….. арќылы жү зеге асады		Тұ йық тізбек	Тұ йық формула	Тұ йық сан	Индекстік жол	Тұ йық емес тізбек
36.		ТЕ. Кететін шығ ынның формуласы		Zmin=å å CijXij	Z=å å CijXij	Zmin=å å Cij	Zmin=å å Xij	Zmin=å CijXij
37.		ТЕ Солтү стік -батыс тә сілі....... қ олданылады		Бірінші тіректі жоспарды қ ұ ру ү шін	Екінші тіректі жоспарды қ ұ ру ү шін	Соң ғ ы тіректі жоспарды қ ұ ру ү шін	Шешуші элементті табу ү шін	Ү шінші тіректі жоспарды қ ұ ру ү шін
38.		ТЕ Ењ тә уір элемент тә сілі......... қ олданылады		Бірінші тіректі жоспарды қ ұ ру ү шін	Екінші тіректі жоспарды қ ұ ру ү шін	Соң ғ ы тіректі жоспарды қ ұ ру ү шін	Шешуші элементті табу ү шін	Ү шінші тіректі жоспарды қ ұ ру ү шін
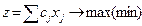
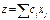
39.		СПЕ. Мақ сатты функцияның формуласы					Z=∑ CJ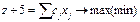
40.		СПЕ. Есептің шарттарын сипаттайтын формула		å aijxJ ≤ = ≥ bi	å xJ ≤ ≥ bi	å aij ≤ ≥ bi	aijxJ ≤ ≥ bi	å aijxJ *bi
41.		СПЕ. аіj... білдіреді.		Техникалық экономикалық коэффициентті	Есептің шешімін	Есептің шартын	Мә ні табылуғ а тиісті айнымалыны	Шектеуді
42.		СПЕ. Xj........ білдіреді		Мә ні табылуғ а тиісті айнымалыны	Техникалық экономикалық коэффициентті	Есептің шешімін	Есептің шартын	Шектеуді
43.		СПЕ. Bi......... білдіреді		Ресурстың кө лемін	Мә ні табылуғ а тиісті айнымалыны	Техникалық экономикалық коэффициентті	Есептің шешімін	Есептің шартын
44.		СПЕ. Кіндіктес есептің мағ ынасы		Ресурстың қ ұ ндылығ ын білдіреді	Ресурсты тиімді пайдалануды білдіреді	Кететін шығ ынның минималын	Пайданың мах-мын	Есептің шешімінің болмайтындығ ын
45.		СПЕ. Есепті шығ ару ү шін.. тә сілін пайдаланады		Симплекс	Солтү стік-батыс	Минимал элемент	Диагональ	Ең тә уір элемент
46.		СПЕ. Тиімділік критериі ол-		Бә рі дұ рыс	Пайданың максимумы	Кірістің максимумы	Шығ ынның минимумы	Уақ ыттың минимумы
47.		СПЕ. Ресурстың толық жұ мсалатынын білдіретін формула		å aijxJ =bi	aijxJ =bi	å ai =bi	å aijxJ =X	aijxJ =å bi
48.		СПЕ. Ресурстың толық жұ мсалмау мү мкіндігін білдіретін формула		å aijxJ ≤ bi	å aijxJ ≥ bi	å ai ≤ ≥ bi	å xJ ≤ ≥ bi	å aijxJ =bi
49.		СПЕ. Xj -ө німiнің тиімді екенін білдіретінін формула		å aijуJ =сj	å aijxJ ≤ c i	å aij ≤ bi	aijxJ ≤ bi	å aijxJ ≤ c
50.		СПЕ. Xj ө німiнің тиімді емес екенін білдіретінін формула		å aijуJ > сj	å aijуJ < сj	å aijуJ =сj	å ai =bi	aijxJ =å bi
51.		СПЕ. Мақ сатты функцияның геометриялық сипаттамасы		Шешуші тү зу	Кө пбұ рыш	Кө пбұ рыштың қ абырғ асы	Симплекс	Коллинеар вектор
52.		СПЕ. Есептің шарттарының геометриялық сипаттамасы		Кө пбұ рыш	Градиент вектор	Кө пбұ рыштың қ абырғ асы	Шешуші тү зу	Нү кте
53.		ТЕ. Ашық модельді жабық модельге... арқ ылы айналдырады		Жасанды айнымалылар	Солтү стік батыс тә сілі	Диагональ тә сілі	Минимал элемент тә сілі	Нү кте
54.		ТЕ. Жасанды айнымалынының тарифтері…. Тең		0-ге	1-ге	Теріс санғ а	Бос мү шеге	Ү лкен санғ а
55.		ТЕ. Потенциал …. анық тайды		Жатық жол мен бағ ананы сипаттайтын санды	Диагоналда жатқ ан санды	Теріс сандарды	Оң сандарды	Характеристиканы
56.		ТЕ. Тиімділік критериі……арқ ылы анық талады		Характеристикалар	Индекстік жол	Потенциалдар	Тарифтер	Шешім
57.		Ө ндірістік функция(Ө Ф) …. арасындағ ы қ арым қ атынасты сипаттайды		Шығ ын мен ө нім	Адам кү ші мен ресурстар	Адам мен капиталдың	Шығ ын мен ресурстардың	Ғ ылым мен ресурстардың
58.		Ө ндірістік функция …… модельге жатады		Регрессиялық	Баланстық	Детерминантты	Стохастикалық	Динамикалық
59.		Y= a+b1x1+…..+bnxn ө ндірістік функциясы берілген мұ ндағ ы b1….bn		Параметр	Фактор	Есептің шешімі	Айнымалы	Шешім
60.		Y= a+b1x1+…..+bnxn ө ндірістік функциясы берілген мұ ндағ ы х1….хn		Фактор	Параметр	Есептің шешімі	Айнымалы	Шешім
61.		Ө Ф параметрларын табу ү шін қ андай тә сіл қ олданады		Кіші квадраттар	Симплекс	Ү лкен квадраттар	Орташа	Монте Карло
62.		Лагранж кө бейткіштері ….. ү шін қ олданылады		СЕПЕ шығ ару ү шін	Қ иылысу нү ктелерін табу	Шешуші элементті табу	Есептің шарттарын қ ұ ру	СПЕ шығ ару ү шін
63.		СЕПЕ ……болғ анда ғ ана қ ұ рылады		Мақ сатты функция немесе есеп шарттары сызық тық емес	Шешуші элемент теріс	Базистік айнымалы сызық тық емес	Есептің шарттары тең деу	Элемент теріс болғ анда
64.		Кобб-Дуглас функциясын кө рсет		Y=a0Ka1La2	Y=a0Ka1L	Y=a0La2	Y=Ka1La2	Y=a0K*L
65.		Y=a0Ka1La2 ө ндірістік функцияағ ы а1 ……. сипаттайды		Капиталдың 1% -ке ө згергендегі Ү –тің қ анша % -ө згеретінін	Ең бектің 1% -ке ө згергендегі Ү –тің қ анша % -ө згереті-нін	Ең бек пен каптиалдың 1% -ке ө згергендегі Ү –тің қ анша % -ө згереті-нін	Ең бектің 10% -ке ө згергендегі Ү –тің қ анша % -ө згереті-нін	Капиталдың 10% -ке ө згергендегі Ү –тің қ анша % -ө згеретінін
66.		Y=a0Ka1La2 ө ндірістік функцияағ ы а2 ……. сипаттайды		Ең бектің 1% -ке ө згергендегі Ү –тің қ анша % -ө згереті-нін	Капиталдың 1% -ке ө згергендегі Ү –тің қ анша % -ө згеретінін	Ең бек пен каптиалдың 1% -ке ө згергендегі Ү –тің қ анша % -ө згереті-нін	Ең бектің 10% -ке ө згергендегі Ү –тің қ анша % -ө згереті-нін	Капиталдың 10% -ке ө згергендегі Ү –тің қ анша % -ө згеретінін
67.		Ө Ф графигі …….. сипатталады		Изокванталармен	Изокосталармен	Кө пбұ рышпен	Симплекспен	Осьпен
68.		СПЕ шығ аратын программаны ата		Поиск решения	WORD	PAJEMAKER	COREL DRAW	PHOTOSHOP
69.		“Поиск решения ” программасы. Бірінші терезешеде ………. адресі орналасқ ан		Мақ сатты функцияның	Айнымалылардың	Шектеулердің	Параметрлардың	Жалаушалардың
70.		“Поиск решения ” программасы. Екінші терезешеде ………. адресі орналасқ ан		Айнымалылардың	Мақ сатты функцияның	Параметрлардың	Шектеулердің	Жалаушалардың
71.		“Поиск решения ” программасы. Ү шінші терезешеде ………. адресі орналасқ ан		Шектеулердің	Айнымалылардың	Мақ сатты функцияның	Параметрлардың	Жалаушалардың
72.		“Поиск решения ” программасы. Есептің шешімдері …орналасқ ан		”Отчет по результатам”-да	“Отчет по пределам”-да	“Отчет по устойчивости”-да	“Отчет по переменным” –да	“Отчет по ограничениям”-да
73.		“Поиск решения ” программасы. Айнымалы-лардың ең тө менгі мә ндері		“Отчет по пределам”-да	”Отчет по результатам”-да	“Отчет по устойчивости”-да	“Отчет по переменным” –да	“Отчет по ограничениям”-да
74.		“Поиск решения ” программасы. Айнымалы-лардың ең жоғ арғ ы мә ндері		“Отчет по пределам”-да	”Отчет по результатам”-да	“Отчет по устойчивости”-да	“Отчет по переменным” –да	“Отчет по ограничениям”-да
75.		“Поиск решения ” программасы. Шешімдердің мә ндеріне ық пал ету... сипатталғ ан		“Отчет по устойчивости”-да	“Отчет по пределам”-да	”Отчет по результатам”-да	“Отчет по переменным” –да	“Отчет по ограничениям”-да
76.		“Поиск решения ” программасы. Тапшы (дефицит) ресурстардың бағ асы …….сипатталғ ан		Теневые цены	Солнечные цены	Дефицитные цены	Недифицитные	Высокие цены
77.		“Поиск решения ” программасы. Тапшы емес ресурстардың бағ асы …….тең		0-ге	1-ге	-1-ге	0, 1-ге	2-ге
78.		СПЕ. Мақ сатты функция мах-ғ а негізделген Шешуші бағ ананы табу ү шін …..тaң дайды		Индекстік жолдағ ы теріс мә ндердің абсолютті ү лкен мә нін	Индекстік жолдағ ы оң мә ндердің абсолютті ү лкен мә нін	Индекстік жолдағ ы теріс мә ндердің абсолютті кіші мә нін	Индекстік жолдағ ы оң мә ндердің абсолютті кіші мә нін	Шешуші элементті
79.		СПЕ. Мақ сатты функция min-ғ а негізделген Шешуші бағ ананы табу ү шін …..тң дайды		Индекстік жолдағ ы оң мә ндердің абсолютті ү лкен мә нін	Индекстік жолдағ ы теріс мә ндердің абсолютті ү лкен мә нін	Индекстік жолдағ ы теріс мә ндердің абсолютті кіші мә нін	Индекстік жолдағ ы оң мә ндердің абсолютті кіші мә нін	Шешуші элементті
80.		Симплекстік тә сіл. Шешуші элемент …….орналасады		Шешуші бағ ана мен шешуші жолдың қ иылысында	Шешуші бағ ана мен индекстік жолдың қ иылысында	Индекстік жол мен шешуші жолдың қ иылысында	Бос мү шелер бағ анасында	Айнымалылар бағ анасында
81.		Симплекстік тә сіл. Шешуші жолды табу ү шін		Бос мү шелерді шешуші бағ анадағ ы сандарғ а бө леді	Бос мү шелерді шешуші жолдағ ы сандарғ а бө леді	Бос мү шелерді 2-ге бө леді	Бос мү шелерді индекстік жолдағ ы сандарғ а бө леді	Бос мү шелерді индекстік жолдағ ы сандарғ а кө бейтеді
82.		ТЕ тиімді маршруттардың саны......формуласымен анық талады		n+m-1	n-m-1	n+m+1	n+m	m-1
83.		Икемділік коэффициенті ……. сипаттайды		пайыздық ық палдың мө лшерін	Бірліктік ық палдың мө лшерін	Тонналық ық палдың мө лшерін	Кг-дық ық палдың мө лшерін	Км-лық ық палдың мө лшерін
84.		СБМ.1-квадрантта не тұ рады		Салалардың ө зара байланысы	Соң ғ ы ө нім	Ұ лттық табыс	Шығ ын	Салалардың саны
85.		СБМ.ІІ-квадрантта не тұ рады		Соң ғ ы ө нім мен жалпы ө нім	Салалардың ө зара байланысы	Ұ лттық табыс	Шығ ын	Салалардың саны
86.		СБМ.ІІІ-квадрантта не тұ рады		Қ ұ ндық қ ұ рылым	Соң ғ ы ө нім	Салалардың ө зара байланысы	Шығ ын	Салалардың саны
87.		Детерминантты модель айнымалылардың арасындағ ы байланыстың... сипаттайды		Функционалдылығ ын	Стохастикалық тығ ын	Динамикалық тығ ын	Статикалық тығ ын	Корреляциялығ ын
88.		Стохастикалық моделдерде…. пайдаланады		Ық тималдар теориясын	Интегралдар теориясын	Дифференциалдар теориясын	Динамика теориясын	Статика теориясын
89.		Динамикалық моделдерде…. пайдаланады		Уақ ытқ а тә уелділік теориясын	Ық тималдар теориясын	Интегралдар теориясын	Статика теориясын	Дифференциалдар теориясын
90.		Статикалық моделдерде…. пайдаланады		Уақ ыттың бір мезетіндегі тә уелділікті	Ық тималдар теориясын	Интегралдар теориясын	Дифференциалдар теориясын	Уақ ыттың бірнеше мезетіндегі тә уелділікті
91.		Экономиканы тұ тастай сипатайтын модельді… деп атайды		Макроэкономикалық	Микроэкономикалық	Ө ндірістік функция	Қ олданбалы	Теориялық
92.		Экономикалық субъектінің (объектінің) іс –қ имылын зерттейтін модельді … деп атайды		Микроэкономикалық	Макроэкономикалық	Ө ндірістік функция	Қ олданбалы	Теориялық
93.		Экономикалық субъектінің (объектінің) параметрларын анық тайтын модельді ……. деп атайды		Қ олданбалы	Микроэкономикалық	Макроэкономикалық	Ө ндірістік функция	Теориялық
94.		Y= A+BX ол... модель деп аталады		Сызық ты	Сызық ты емес	Тұ рақ ты емес	Гиперболалық	Параболалық
95.		Y=a+1/x2 ол….. модель деп аталады		Сызық ты емес	Сызық ты	Тұ рақ ты емес	Гиперболалық	Параболалық
96.		Экономикалық іс-қ имылдың тиімділігін ……..модель зерттейді		Оптималды	Микроэкономикалы	Теориялық	Макроэкономикалық	Қ олданбалы
97.		Сандық заң дылық тар мен қ арым- қ атынасты зерттейтін модель		эконометриялық	Детерминантты	Стохастикалық	Динамикалық	Статикалық
98.		Ресурс пен оғ ан қ ажеттілікті сипаттайтын модель		Баланстық	Детерминантты	Стохастикалық	Динамикалық	Статикалық
99.		СПЕ. Канондық кү йге айналдыратын қ осымша айнымалы…сипаттайды		Пайдаланылмағ ан ресурстарды	Пайдаланылғ ан ресурстарды	Ресурстардың кө лемін	Есептің шешімдерін	Шешімдер кө лемін
100.		СПЕ.Геометриялық топшылау қ ай квадрантта жатады.
101.		СПЕ. Есептердің шартында ³ таң басы болса онда шешім …. тә сілі қ олданылады		М-	Кіші квадраттар	Солтү стік батыс	Диагональ	Ең тә уір
102.		СПЕ. Индекстік жол …..анық тайды		Тиімділік критериін	Есептің шешімдерін	Базистік айнымалыларды	Қ иылысу нү ктелерін	Шығ ынды
103.		Ө нім мен шығ ынның арасындағ ы функция …….деп аталады		ө ндірістік	Гиперболалық	Периодты	Ү зіліссіз	Шығ ынды
104.		Ресурстың қ ұ ндылығ ын …… есеп арқ ылы анық тайды		Кіндіктес	Тасымал	Регрессиялық	Динамикалық	Статикалық
105.		ТЕ. Жатық жолдар мен бағ аналарды сипаттайтын сандарды ……….деп атайды		Потенциалдар	Есептің шешімдері	Характеристикалар	Тасылатын жү ктің мө лшері	Маршрут саны
106.		Y=a0Ka1La2 ….. функциясы деп аталады		Кобб-Дуглас	Леонтьев	Кейнс	Филлипс	Энгель
107.		Тренд дегеніміз		Ұ зақ мерзімді ағ ым	Қ ысқ а мерзімді ағ ым	Орта мерзімді ағ ым	Ресурстың кө лемі	Тә сіл
108.		Маусымдық фактор дегеніміз		Бір жылдың ішінде болатын ауытқ у	Бір айдың ішінде болатын ауытқ у	Бір кварталдың ішінде болатын	Бірнеше жылдың ішінде болатын ауытқ у	Бір кү ннің ішінде болатын ауытқ у
109.		Имитациялық модель ол		ЭЕМ арқ ылы зерттелетін модель	Тең деулер арқ ылы зерттелетін модель	График арқ ылы зерттелетін модель	Айнымалы арқ ылы ерттелетін модель	Шартты арқ ылы ерттелетін модель
110.		Сызық тық модельді ата		У=5+3х	У= X2	Y= a+b/x	Y=a+b*x+cx2	Y=1/x
111.		Микроэкономикалық модель дегеніміз		Фирманың іс-қ имылын сипаттау	Жаппай қ ызмет кө рсетуді сипаттау	Тасымалды сипаттау	Инфляцияны сипаттау	Жұ мыссыздық ты сипаттау
112.		Модельдеудің І –кезең і		Модельді қ ұ ру	Модельді қ олдану	Модельден алынғ ан білімді тү пнұ сқ ағ а кө шіру	Объектіні басқ арудың теориясын жасақ тау	Есептеу
113.		Модельдеудің І І –кезең і		Модельді қ олдану	Модельді қ ұ ру	Модельден алынғ ан білімді тү пнұ сқ ағ а кө шіру	Объектіні басқ арудың теориясын жасақ тау	Есептеу
114.		Модельдеудің І І І –кезең і		Модельден алынғ ан білімді тү пнұ сқ ағ а кө шіру	Модельді қ олдану	Модельді қ ұ ру	Объектіні басқ арудың теориясын жасақ тау	Есептеу
115.		Модельдеудің І V –кезең і		Тү пнұ сқ аны басқ арудың теориясын жасақ тау	Модельді қ олдану	Модельді қ ұ ру	Модельден алынғ ан білімді тү пнұ сқ ағ а кө шіру	Есептеу
116.		Техникалық экономикалық коэффициентті ата		aij	cij	xij	bj	ai
117.		Симплекс тә сілі ……..ү шін қ олданылады		СПЕ шығ ару	Интегралдық есепті	Дифференциалдық есеп	Тең деуді шешу	СЕПЕ шығ ару
118.		ТЕ. М- саны ол		Ү лкен сан	Кіші сан	О -ге тең	1-ге тең	Теріс сан
119.		Сызық тық модельді кө рсет		Y= a+b*x	У= X2	Y= a+b/x	Y=a+b*x+cx2	Y=1/x
120.		Уақ ыттың бір мезетіндегі кү йді сипаттайтын модель		Статикалық	Динамикалық	Микроэкономикалық	Макроэкономикалық	Детерминантты
121.		Уақ ытқ а тә уелді болатын модельді сипаттайтын модель		Динамикалық	Статикалық	Микроэкономикалық	Макроэкономикалық	Детерминантты
122.		Нә тижесі анық талғ ан факторларғ а тә уелді болатын модель		Детерминантты	Динамикалық	Статикалық	Микроэкономикалық	Макроэкономикалық
123.		Жү йе дегеніміз		Бір біріне тә уелді элементтер жиыны	Бір біріне тә уелсіз элементтер жиыны	0-ден тұ ратын жиын	1-ден тұ ратын жиын	Айнымалылардың қ арым қ атынасы
124.		Стохастикалық модель дегеніміз		Нә тижесі кездейсоқ шамадан тә уелді болатын модель	Бір біріне тә уелсіз элементтер жиыны	0-ден тұ ратын жиын	1-ден тұ ратын жиын	Айнымалылардың қ арым қ атынасы
125.		Қ олданбалы модель		Нақ ты бір экономикалық объектіге қ олданылатын модель	Нә тижесі кездейсоқ шамадан тә уелді болатын модель	Айнымалылардың қ арым қ атынасы	Модельден алынғ ан білімді тү пнұ сқ ағ а кө шіру	Динамикалық модель
126.		Теориялық модель ол		Экономикалық процесстердің жалпы қ асиеттері мен заң дылық тарын зерттейтін модель	Нә тижесі кездейсоқ шамадан тә уелді болатын модель	Айнымалылардың қ арым қ атынасы	Модельден алынғ ан білімді тү пнұ сқ ағ а кө шіру	Динамикалық модель
127.		ТЕ. Тариф ол….		Cij	Aj	Xij	Bi	Ai
128.		ТЕ.Жабық модельді сипаттайтын формула		å Bj =å Ai	å Bj ¹ å Ai	å Bj > å Ai	å Bj < å Ai	å Bj +å Ai
129.		ТЕ. Kері тасымалды сипаттайтын формула		Xij ³ 0	Xij < 0	Xij ³ -5	å Bj < å Ai	Bj +å Ai
130.		CЕПЕ болу ү шін ………керек		Мақ сатты функцияның немесе есеп шарттарының сызық ты болмауы	Мақ сатты функцияның немесе есеп шарттарының теріс болмауы	Мақ сатты функцияның немесе есеп шарттарының дифференциалды болмауы	Мақ сатты функцияның немесе есеп шарттарының интегралды болмауы	Мақ сатты функцияның немесе есеп шарттарының интегралды болуы
131.		СПЕ. Есептің шарттары ……тұ рады		Тең сіздіктер мен тең деулерден	Сандардан	айнымалылардан	Мақ сатты функциядан	Коэффициенттерінен
132.		Кіндіктес есептің шарттарының саны тура есептің ……..тең		Айнымалыларына	Шарттарына	Амалдарына	Коэффициенттеріне	Максатты функциясына тең
133.		Кіндіктес есептің айнымалыларының саны тура есептің ……..тең		Шарттарына	Айнымалыларына	Бос мү шелердің	Коэффициенттеріне	Базистік айнымалыларына тең
134.		Кіндіктес есептің мақ сатты функциясының коэффициенттері тура есептің ……..тең		Бос мү шелерінің санына	Айнымалыларына	Базистік айнымалыларына	Коэффициенттеріне	Шарттарына
135.		Кіндіктес есептің бос мү шелері тура есептің ……..тең		Мақ сатты функциясының коэффициенттеріне	Бос мү шелерінің	Айнымалыларына	Базистік айнымалыларына	Элементтердің санына
136.		ЭММ ү лес қ осқ ан ғ алымдар		Бә рі дұ рыс	Немчинов	Конторович	Данциг	Ефимов
137.		Шектеулер дегеніміз		Есептің шарттары	Мақ сатты функция	Айнымалылар	Тең деудің шешімдері	Тең сіздіктің шешімдері
138.		Модельдің идентификациясы ол		Параметрлардың дә л анық талуы	Параметрлардың дә л анық талмауы	Айнымалылардың санын анық тау	Шектеулердің санын анық тау	Коэффициенттердің санын анық тау
139.		“Поиск решения” программасы. Теневые цены деген...анық тайды		Тапшы ресурстардың бағ асын	Тапшы емес ресурстардың бағ асын	Айнымалылардың санын	Шектеулердің санын	Коэффициенттердің санын
140.		Поиск решения программасы …..анық тайды		Оптималды моделдердің параметрларын	Статикалық моделдердің параметрларын	Динамикалық моделдердің параметрларын	Макроэкономикалық моделдердің параметрларын	Микроэкономикалық моделдердің параметрларын
141.		ТЕ. n+m-1 формуласы …..анық тайды		Тиімді маршруттардың санын	Тиімсіз маршруттардың санын	Бос клеткалардың санын	Жалпы маршруттардың санын	Микроэкономикалық моделдердің параметрларын
142.		Модельдің адекваттығ ы деп оның ….. айтады		Шынайылығ ын	Жалғ андығ ын	Тұ рақ тылығ ын	Тұ рақ сыздығ ын	Жылдамдығ ын
143.		Экзогенді деп …. айнымалыны айтады		Мә ндері алдын-ала берілген	Мә ндері есептелетін отыратын	Мә ндері 0-ге тең	Базистік	Еркін
144.		Эндогенді деп … айнымалыны айтады		Мә ндері есептеліп отыратын	Мә ндері алдын-ала берілген	Мә ндері 0-ге тең	Базистік	Еркін
145.		Бірлік матрица деп……матрицаны айтады		Тек диагоналы 1-ден тұ ратын	Диагоналы 1-ден тұ рмайтын	Барлық элементтері 1-ден	Анық тауышы 1-ге тең	Рангы 1-ге тең
146.		Нолдік матрица деп ……матрицаны айтады		Барлық элементтері 0-ден тұ ратын	Тек диагоналы 0-ден тұ ратын	Диагоналы 0-ден тұ рмайтын	Анық тауышы 0-ге тең	Рангы 0-ге тең
147.		Кері матрица деп ……матрицаны айтады		Тура матрицамен кө бейтіндісі бірлік матрица болатын	Тура матрицамен кө бейтіндісі нольдік матрица болатын	Элементері кері саннан тұ ратын	Элементері теріс саннан тұ ратын	Анық тауышы 1-ге тең
148.		Сызық тық модельдің графигі ….. болады		Тү зу	Қ исық	Парабола	Гипербола	Шең бер
149.		Сызық тық емес модельдің графигі ….. болады		Қ исық	Тү зу	Диаграмма	Гистограмма	Кесте
150.		СПЕ. Ресурстың кө лемін ата		Bi	Cij	Xij	Zmax	Zmin
151.		Уақ ыт қ атарлары деп ……айтады		Бір экономикалық объектінің ә ртү рлі уақ ыт мезетіндегі кө рсеткіштер жиыны	Бірнеше экономикалық объектінің ә ртү рлі уақ ыт мезетіндегі кө ө рсеткіштер жиыны	Бір экономикалық объектінің бір уақ ыт мезетіндегі кө ө рсеткіштер жиыны	Бірнеше экономикалық объектінің бір уақ ыт мезетіндегі кө ө рсеткіштер жиыны	формуланы
152.		Бір экономикалық объектінің ә ртү рлі уақ ыт мезетіндегі кө рсеткіштер жиыны……деп айтады		Уақ ыт қ атарлары	Қ иылысқ ан деректер	Тренд	Баланс	Есепті
153.		Кең істік деректер деп……айтады		Бірнеше экономикалық объектінің бір уақ ыт мезетіндегі кө рсеткіштер жиыны	Бір экономикалық объектінің ә ртү рлі уақ ыт мезетіндегі кө ө рсеткіштер жиыны	Бір экономикалық объектінің бір уақ ыт мезетіндегі кө ө рсеткіштер жиыны	Бірнеше экономикалық объектінің ә ртү рлі уақ ыт мезетіндегі кө ө рсеткіштер жиыны	Есепті
154.		Бірнеше экономикалық объектінің бір уақ ыт мезетіндегі кө рсеткіштер жиынын...... деп айтады		Қ иылысқ ан деректер	Уақ ыт қ атарлары	Тренд	Баланс	Есепті
155.		Экономикалық деректер деп…… айтады		Белгілі бір уақ ыттағ ы экономикалық объектілердің іс-қ имылын сипаттайтын кө рсеткіштер жиынын	Белгілі бір уақ ыттағ ы экономикалық объектілердің техникалық жағ дайын сипаттайтын деректер жиынын	Белгілі бір уақ ыттағ ы экономикалық объектілердің ә леуметтік жағ дайын сипаттайтын деректер жиынын	Белгісіз бір уақ ыттағ ы экономикалық объектілердің ә леуметтік жағ дайын сипаттайтын деректер жиынын	формуланы
156.		Егер модель уақ ытқ а тә уелді болса ол …….модель		Динамикалық	Статикалық	Стохастикалық	Детерминантты	Функционалды
157.		Кіндіктес есептің матрицасы тура есептің …….матрицасына тең		Транспонентті	Кері	Бірлік	Нольдік	Анық тауыш
158.		СПЕ Тиімділік критериінің математикалық жазылуы		Мақ сатты функцияны	Есептің шарттарын	Коэффициентерін	Тең сіздікті	Қ осымша айнымалыны
159.		СПЕ. Симплекс тә сілін қ олданғ ан кезде …..ә дісі пайдаланылады		Жордан-Гаусс	Кобб-Дуглас	Кіші квадраттар тә сілі	Графикалық	Матрицалық
160.		СПЕ қ осымша айнымалылардың коэффициенттері … тең		1-ге	0-ге	2-ге	3-ке	4-ке
161.		СПЕ Қ осымша айнымалылар ………сипатталады		Пайдаланылмағ ан ресурстарды	Пайдаланылғ ан ресурстарды	Шарттарды	Ұ тымды бағ аларды	Кеткен шығ ынды
162.		Тү пнұ сқ аның тү рін тү сін тұ рпатын сипаттайтын модельді …….. атайды		физикалық	Абстрактілік	Геометриялық	Информациялық	Таң балық
163.		Тү пнұ сқ аның қ асиетін таң балар арқ ылы сипаттайтын модельді …….. атайды		Абстрактілік	физикалық	Материалдық	Муляж	Манекен
164.		ТЕ. Жабдық таушылар саны … тең		m	n	Ai	Bj	Xij
165.		TE. Тұ тынушылар саны ….. тең		n	m	Ai	Bj	Xij
166.		ТЕ. Жабдық таушыдағ ы заттың мө лшері ….. тең		Ai	m	n	Bj	Xij
167.		ТЕ. Тұ тынушығ а қ ажет заттың мө лшері		Bj	Ai	m	Xij	n
168.		СПЕ. Градиент …….анық тайды		Шешуші тү зуді	Кө пбұ рышты	Симплексті	Шешуші элементті	Есептің шешімін
169.		СПЕ. Есеп канондық кү йде болса онда шарт таң басымен сипатталады		=	<	£	¹	³
170.		СПЕ. Есеп стандарттық кү йде болса онда шарт.... таң басымен сипатталады		£	=	<	¹	*
171.		СПЕ. Мах(min) табу ү шін шешуші тү зу ……. Бағ ытымен жылжытылуы керек		Градиент	У осімен	Х осімен	Симплекстің бағ ытымен	Қ абырғ аның бойымен
172.		ТЕ. Ашық модель жабық модельге … арқ ылы жеткізіледі		Жасанды айнымалылар арқ ылы	Бірлік элемент арқ ылы	Бірлік матрица арқ ылы	Нолдік матрица арқ ылы	Қ осымша функция арқ ылы
173.		Баланстық модель …. анық талады		Тең деулер жү йесімен	Тең сіздіктер жү йесімен	Коэффициенттер жү йесімен	Функциялар жү йесімен	Айнымалылар жү йесімен
174.		Салааралық баланс неше квадранттан тұ рады
175.