Схема с автоматическим выбором шага по заданной точности

1. Один из вариантов вычисления интеграла с заданной точностью:

1) Задают первоначальное число площадок m и вычисляют значение S1

2) Число площадок удваивают m=m*2

3) Вычисляют значение интеграла S2

4) Проверяют выполнение неравенства:

Если выполняется 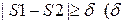- заданная погрешность), то S1=S2

шаг h уменьшают вдвое: m=m*) и расчет повторяют: переход к пункту 3.

5) Если нет, заданная точность достигнута: печать S2, m – финальное число площадок, d - заданная погрешность

2. Анализ приведенных формул показывает, что точное значение интеграла находится между значениям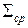и и 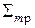, при этом имеет место соотношение

(3.11)

Это соотношение часто используется для контроля погрешности вычислений. Расчет начинается с m =2 и производится по двум методам, в результате получают 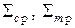. Если 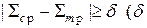- заданная погрешность), то шаг h уменьшают вдвое (m=m× 2) и расчет повторяют. Если точность достигается, то окончательное значение интеграла получается по формуле 3.11. При существенном уменьшении шага h начинают сказываться ошибки округления, поэтому шаг должен быть ограничен снизу некоторой величиной, зависящей от разрядной сетки ЭВМ (m£ n –максимально допустимое число площадок).

Варианты заданий

Создать и отладить программу расчета интеграла с заданной точностью.

При использовании алгоритма вычисления интеграла с автоматическим выбором шага по данной точности расчет произвести для d= 0.01, 0.001, 0.0001 и получить зависимость m(d).

Вычислите интеграл по формуле Симпсона для m=100 и сравните полученный результат со значением интеграла, полученного методом с автоматическим выбором шага интегрирования.

Таблица 3.1

N	Функция f(x)	Интервал	Значение	Метод
a	b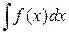
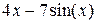
		-2		5.983	левых прямоугольников
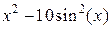
				-6.699	правых прямоугольников
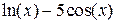
				8.896	средних прямоугольников
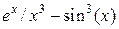
				6.118	трапеций
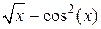
				6.067	метод Симпсона
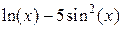
				-3.367	левых прямоугольников
				0.100	правых прямоугольников
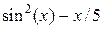
				0.153	средних прямоугольников
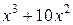
		-8		713.3	трапеций
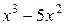
		-2		-69.42	метод Симпсона
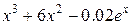
		-5		167.6	левых прямоугольников
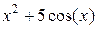
		-1		22.09	правых прямоугольников
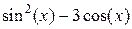
				3.533	средних прямоугольников
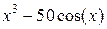
		-2		154.73	трапеций
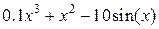
		-4		20.375	метод Симпсона

Контрольные вопросы

1. Дайте геометрическую интерпретацию методов прямоугольников: средних, трапеций, Симпсона.

2. Дайте геометрическую интерпретацию метода трапеций.

3. Дайте геометрическую интерпретацию метода Симпсона.

4. Какой порядок погрешности имеют эти методы?

5. Суть алгоритма вычисления интеграла с автоматическим выбором шага интегрирования.