
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод деления отрезка пополам
|
|
Все вышеописанные методы могут работать, если функция f(x) является непрерывной и дифференцируемой вблизи искомого корня. В противном случае они не гарантируют получение решения.
Для разрывных функций, а также. если не требуется быстрая сходимость, для нахождения простого корня на интервале (a, b) применяют надежный метод деления отрезка пополам. Его алгоритм основан на построении рекуррентной последовательности по следующему закону: в качестве начального приближения выбираются границы интервала, на котором точно имеется один простой корень 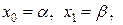 далее находится его середина
далее находится его середина 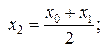 очередная точка x3 выбирается как середина того из смежных с x2 интервалов
очередная точка x3 выбирается как середина того из смежных с x2 интервалов 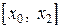 или
или 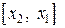 , на котором находится корень. В результате получается следующий алгоритм метода деления отрезка пополам:
, на котором находится корень. В результате получается следующий алгоритм метода деления отрезка пополам:
1. Вычисляем 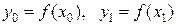 .
.
2. Вычисляем 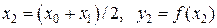 .
.
3. Если 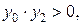 тогда
тогда 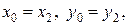
иначе 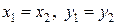 .
.
4. Если  тогда повторять с п.2.
тогда повторять с п.2.
5. Вычисляем 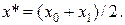
6. Конец.
За одно вычисление функции погрешность уменьшается вдвое, то есть скорость сходимости невелика, однако метод устойчив к ошибкам округления и всегда сходится.
Варианты заданий
1. По схеме, приведенной на рис.1.7 создать и отладить программу отделения всех корней функции f(x) на указанном интервале [a, b], в соответствии с полученным вариантом из табл. 1.1.
2. Далее создать программу уточнения корня указанным итерационным методом.
Метод нахождения корня оформить в виде отдельной функции.
Выбрать точность e=10-3, e=10-4, e=10-5. Функция должна проверить правильность определения корня (f(x*) приблизительно равна нулю).
3. Решить уравнение для выбранного интервала методом деления отрезка пополам
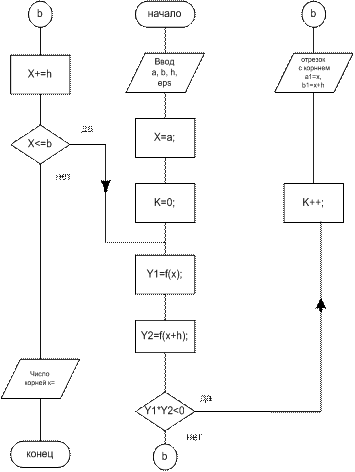
Рис.1.7
Таблица 1.1
| N | f(x) | Интервал | методы | |
| А | B | |||
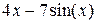
| -2 | Метод деления отрезка пополам | ||
| 2 | 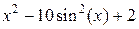
| -1 | Метод секущих | |
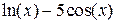
| Метод касательных | |||
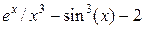
| Метод простой итерации | |||
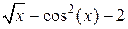
| Метод деления отрезка пополам | |||
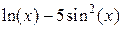
| Метод секущих | |||

| Метод касательных | |||
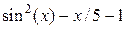
| -4 | Метод простой итерации | ||
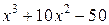
| -12 | Метод деления отрезка пополам | ||
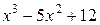
| -2 | Метод секущих | ||
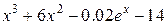
| -6 | Метод касательных | ||
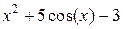
| -4 | Метод простой итерации | ||
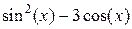
| -7 | Метод деления отрезка пополам | ||
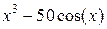
| -4 | Метод секущих | ||
| -4 | Метод касательных | ||